Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the sine-elliptic Mathieu function
ResourceFunction["MathieuEllipticSin"][n, x, q] gives the nth odd Mathieu function sen(x,q). |
Evaluate the se1(x,0) function:
| In[1]:= |
| Out[1]= |
Evaluate se2(2,2) numerically:
| In[2]:= |
| Out[2]= |
Function plots for q=2:
| In[3]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/05cfa962-b1c6-4941-8c2c-f77364f62f6e"]](https://www.wolframcloud.com/obj/resourcesystem/images/83a/83a5b29c-045a-4e5f-8992-2b51992a27c8/4ffa96aba3db88fc.png) |
| Out[3]= | 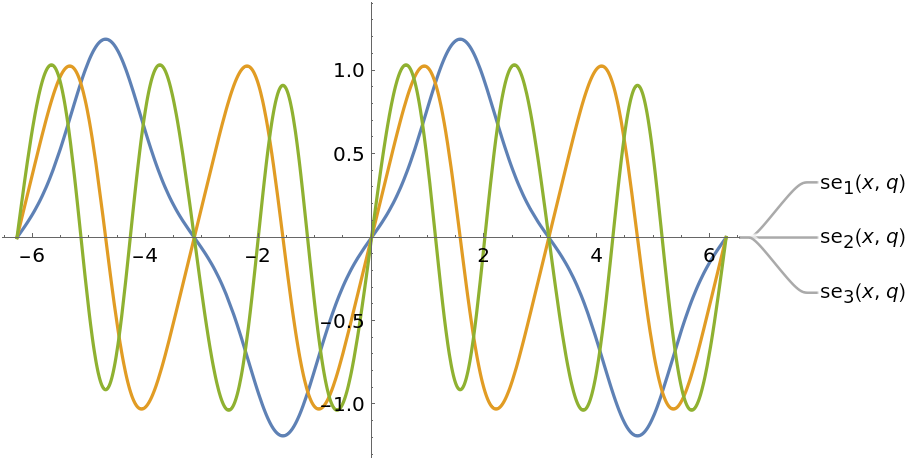 |
Visualize an eigenfunction of the Laplace equation in an ellipse that vanishes at the boundary:
| In[4]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/ac5a5011-564f-4256-ab74-188327565185"]](https://www.wolframcloud.com/obj/resourcesystem/images/83a/83a5b29c-045a-4e5f-8992-2b51992a27c8/4482be58cc56ee54.png) |
| Out[4]= | 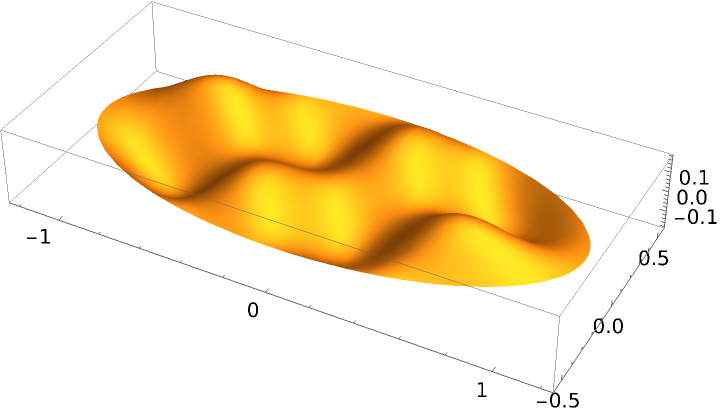 |
This work is licensed under a Creative Commons Attribution 4.0 International License