Function Repository Resource:

MappedTransformedDistribution

Source Notebook

Transform a statistical distribution by applying the same function to all of its arguments

Contributed by: Isaac Chandler and Seth J. Chandler

ResourceFunction["MappedTransformedDistribution"][f,dist]

creates a transformed distribution for which the function f is mapped over all of the arguments.

Details and Options

If the distribution has just one argument, the function f is applied to that argument and not "mapped" over it.

Examples

Basic Examples (3)

Compute the CDF of a product distribution of two binomial distributions in which 1 has been added to each of the arguments:

In[1]:=

CDF[ResourceFunction["MappedTransformedDistribution"][# + 1 &, ProductDistribution[BinomialDistribution[2, 3/5], BinomialDistribution[2, 4/5]]], {x, y}]

Out[1]=

Compute the CDF of a lognormal distribution in which the argument has been negated:

In[2]:=

$CDF[ResourceFunction["MappedTransformedDistribution"][-# &, LogNormalDistribution[\[Mu], \[Sigma]]], -x]$

Out[2]=

Compute the SurvivalFunction of a binomial distribution in which the square root is applied to its argument:

In[3]:=

Out[3]=

Scope (3)

Compute the mean of a mapped transformed distribution of a multivariate discrete distribution:

In[4]:=

Out[4]=

Compute the characteristic function of a mapped transformed distribution of a multivariate symbolic continuous distribution:

In[5]:=

CharacteristicFunction[
ResourceFunction["MappedTransformedDistribution"][Sqrt, ProductDistribution[BetaDistribution[a, b], BetaDistribution[c, d]]], {t1, t2}] // TraditionalForm

Out[5]=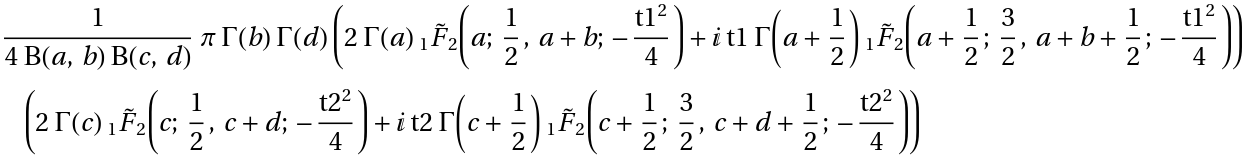

Compute the mean of a mapped transformed distribution of a copula distribution of two binomial distributions:

In[6]:=

$Mean[ResourceFunction["MappedTransformedDistribution"][1/(1 + #)^r &, CopulaDistribution[{"Binormal", -3/10}, {BinomialDistribution[10, 1/5], BinomialDistribution[10, 2/7]}]]]$

Out[6]=

Applications (1)

Plot the CDF of a copula distribution whose components are binomial and each argument of which has been transformed by adding 1 to it:

In[7]:=

Plot3D[Evaluate[
CDF[ResourceFunction["MappedTransformedDistribution"][# + 1 &, CopulaDistribution[{"Binormal", -0.3}, {BinomialDistribution[5, 3/5], BinomialDistribution[5, 4/5]}]], {x, y}]], {x, 0, 6}, {y,
0, 6}, PlotRange -> All, ColorFunction -> "Pastel"]

Out[7]=

Properties and Relations (2)

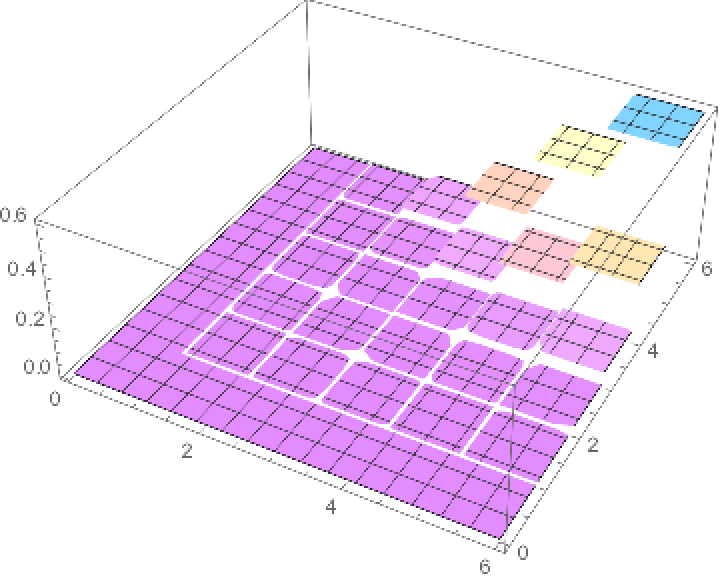If the function mapped over the arguments to a continuous distribution is negation, that is, -#&, the roles of CDF and SurvivalFunction are effectively exchanged:

In[8]:=

Out[8]=

The SurvivalFunction of a discrete distribution evaluated at x is the same as the CDF of the mapped transform distribution evaluated at -(x+1), where the mapped function is -#& and the distribution is defined over integers:

In[9]:=

Out[9]=

Neat Examples (1)

Compute the probability that a person alive at age 61 will be dead before age 71 given that their mortality is determined by a discretized variant of a Gompertz–Makeham mortality function:

In[10]:=

$discreteGompertzMakehamDistribution[a_, b_] := ProbabilityDistribution[{"PDF", CDF[GompertzMakehamDistribution[a, b], t + 1] - CDF[GompertzMakehamDistribution[a, b], t]}, {t, 0, 120, 1}]$