Function Repository Resource:

MapAtPart

Source Notebook

Map different functions at particular positions

Contributed by: Faizon Zaman

ResourceFunction["MapAtPart"][{i₁→f₁,…,i_n→f_n},expr]

applies f_n to the element at position i_n in expr.

ResourceFunction["MapAtPart"][fs]

represents an operator form of ResourceFunction["MapAtPart"] that can be applied to an expression.

Details

The f_i are applied in the order given.

The f_i apply to individual elements as opposed to sequences of elements within the expression.

i can be any part specification supported by MapAt, as well as symbolic parts First, Last, Most, Rest, and Span.

The input expr can have any head, not just List.

Examples

Basic Examples (3)

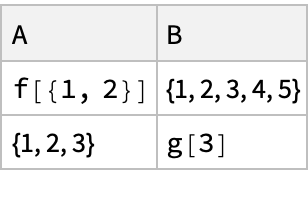
Apply f to the first element of a list and g to the second:

In[1]:=

Out[1]=

Apply func to the value of a Key in an Association:

In[2]:=

Out[2]=

Use the operator form of MapAtPart:

In[3]:=

Out[3]=

Scope (7)

Symbolic Part Specifications (3)

Apply f to the First element of a list and g to the Rest:

In[4]:=

Out[4]=

Apply f to Most of the list and g to the Last element:

In[5]:=

Out[5]=

Apply f to the First element of the list and g to the Span of elements from position 3 onward:

In[6]:=

Out[6]=

Use the shorthand (;;) syntax for Span:

In[7]:=

Out[7]=

MapAtPart on Associations (4)

Apply f to the first value of an Association:

In[8]:=

Out[8]=

Apply f to Most of the values in an Association and g to the Last value of an Association:

In[9]:=

Out[9]=

Use an explicit Key:

In[10]:=

ResourceFunction["MapAtPart"][
{"A" -> f, Key["C"] -> g},
<|
"A" -> Range[2],
"B" -> Range[3],
"C" -> Range[5]
|>
]

Out[10]=

Specify a nested part:

In[11]:=

res = ResourceFunction["MapAtPart"][
{{1, Key["A"]} -> f, {2, Last} -> g},
{
<|"A" -> Range[2], "B" -> Range[5]|>,
<|"A" -> Range[3], "B" -> 3|>
}
]

Out[11]=

In[12]:=

Out[12]=

Properties and Relations (8)

MapAtPart is implemented with Fold and MapAt; use FoldList to see intermediate steps:

In[13]:=

Out[13]=

In[14]:=

Out[14]=

MapAtPart[i→f,expr] is equivalent to MapAt[f,expr,i]:

In[15]:=

Out[15]=

In[16]:=

Out[16]=

Use multiple positions:

In[17]:=

Out[17]=

In[18]:=

Out[18]=

MapAtPart[i→f,expr] is equivalent to SubsetMap[Map[f],expr,i]:

In[19]:=

Out[19]=

In[20]:=

Out[20]=

Use multiple positions:

In[21]:=

Out[21]=

In[22]:=

Out[22]=

MapAtPart[f,expr] is equivalent to Apply[f,expr]:

In[23]:=

Out[23]=

In[24]:=

Out[24]=

A position specification of All is equivalent to MapAt[f,expr,All] and also equivalent to Map[f,expr]:

In[25]:=

Out[25]=

In[26]:=

Out[26]=

In[27]:=

Out[27]=

If the right-hand side of a replacement wraps the bound expression, then ReplaceAt is also equivalent to the above when the part is All:

In[28]:=

$ReplaceAt[{a, b, c, d, e}, el_ :> f[el], All]$

Out[28]=

ReplacePart has access to indices but not elements:

In[29]:=

$ReplacePart[{a, b, c, d, e}, i_ :> Style[i, Bold]]$

Out[29]=

Conversely, MapAtPart has access to the element values, but not their part specifications:

In[30]:=

Out[30]=

To have access to both indices and element, one needs to use intermediate assignment:

In[31]:=

$With[ {expr = {a, b, c, d, e}}, ReplacePart[expr, i_ :> {Style[expr[[i]], Bold], i}] ]$

Out[31]=

MapAtPart statements can be longer than ReplaceAll statements:

In[32]:=

Out[32]=

In[33]:=

$ReplaceAll[list, {odd_?OddQ :> Echo[odd, "Odd Number"], even_?EvenQ :> Echo[even, "Even Number"]}]$

Out[33]=

In[34]:=

$ResourceFunction[ "MapAtPart"][{Position[list, _?OddQ] -> EchoLabel["Odd Number"], Position[list, _?EvenQ] -> EchoLabel["Even Number"]}, list]$

Out[34]=

The resource function SetComplementMap uses explicit positions for the first function:

In[35]:=

positions = {1, 5, 7, 8, 10};
makeBlue = Style[#, Blue] &;
makeRed = Style[#, Red] &;

In[36]:=

Out[36]=

MapAtPart uses explicit positions for all functions:

In[37]:=

Out[37]=

In[38]:=

Out[38]=

In[39]:=

Out[39]=

In[40]:=

Out[40]=

Possible Issues (7)

Functions are applied to individual elements not sublists:

In[41]:=

Out[42]=

A Function specified with shorthand (#&) should be wrapped in parentheses:

In[43]:=

Out[43]=

In[44]:=

Out[44]=

A list of integers is considered a part path:

In[45]:=

Out[45]=

If each integer is meant as an index on the same level then either wrap them in a list, or use Span:

In[46]:=

Out[46]=

In[47]:=

Out[47]=

When specifying an operator form, remember to wrap the function specification in a list. Notice below that All→g is applied to the second argument 2→f:

In[48]:=

Out[48]=

Wrap the specification in List to get an operator form:

In[49]:=

Out[49]=

In[50]:=

Out[50]=

If a preceding function changes the expression's structure, then subsequent functions won't work as expected (especially if the positions in the expression no longer exist):

In[51]:=

$removeEven = Replace[_?EvenQ -> Nothing]; styleGreen = Style[#, Green] &; modifyStructure = {1 ;; 4 -> removeEven, 3 ;; -> styleGreen};$