Function Repository Resource:

ManipulateParametricPlot

Source Notebook

Produce a dynamic interface for a curve being traced out by the tip of a vector

Contributed by: Dennis M Schneider

ResourceFunction["ManipulateParametricPlot"][{f_x,f_y},{t,tmin,tmax}]

produces an animation of the parametric curve (f_x,f_y) being traced out when t runs from tmin to tmax.

Details and Options

In addition to the options of ParametricPlot and the resource function PlotVector, the following options are supported:

"DrawVector"

False

show the path followed by a particle as it moves along the curve

"PointStyle"

specifies a style for the point

VectorStyle

Red

specifies a style for the vector

Examples

Basic Examples

Create a dynamic plot of a vector tracing out a parametric curve:

In[1]:=

$ResourceFunction[ "ManipulateParametricPlot"][{Cos[3 t], Sin[t]}, {t, 0, 2 \[Pi]}, SaveDefinitions -> True]$

Out[1]=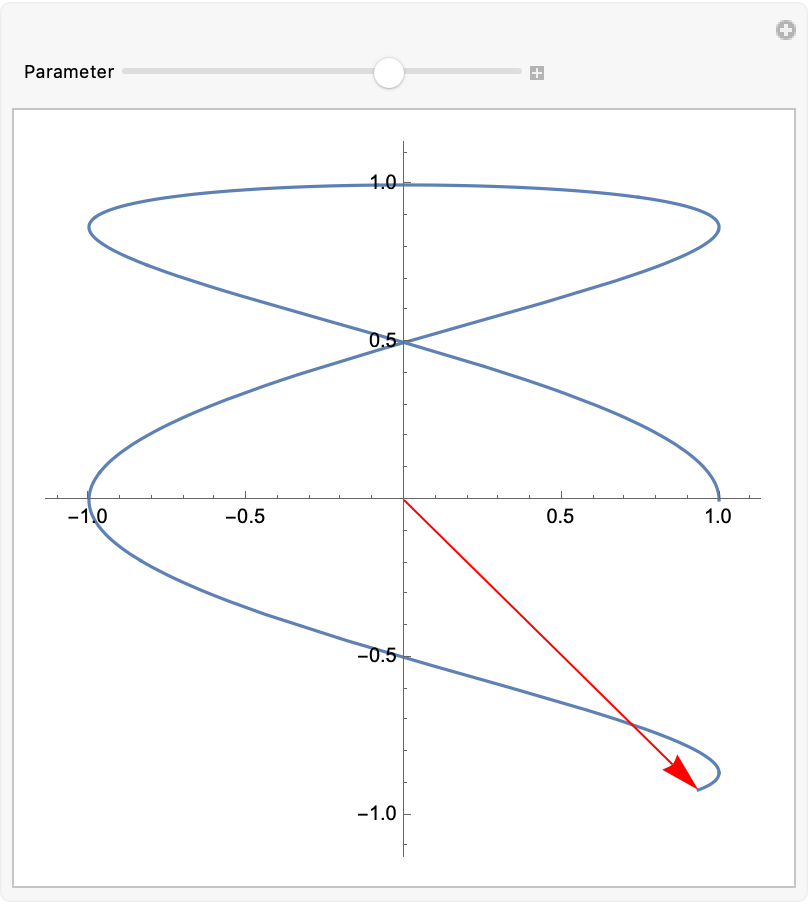

View the motion of an object moving in the plane along a curve:

In[2]:=

$ResourceFunction[ "ManipulateParametricPlot"][{Cos[3 t], Sin[t]}, {t, 0, 2 \[Pi]}, "DrawVector" -> False, SaveDefinitions -> True]$

Out[2]=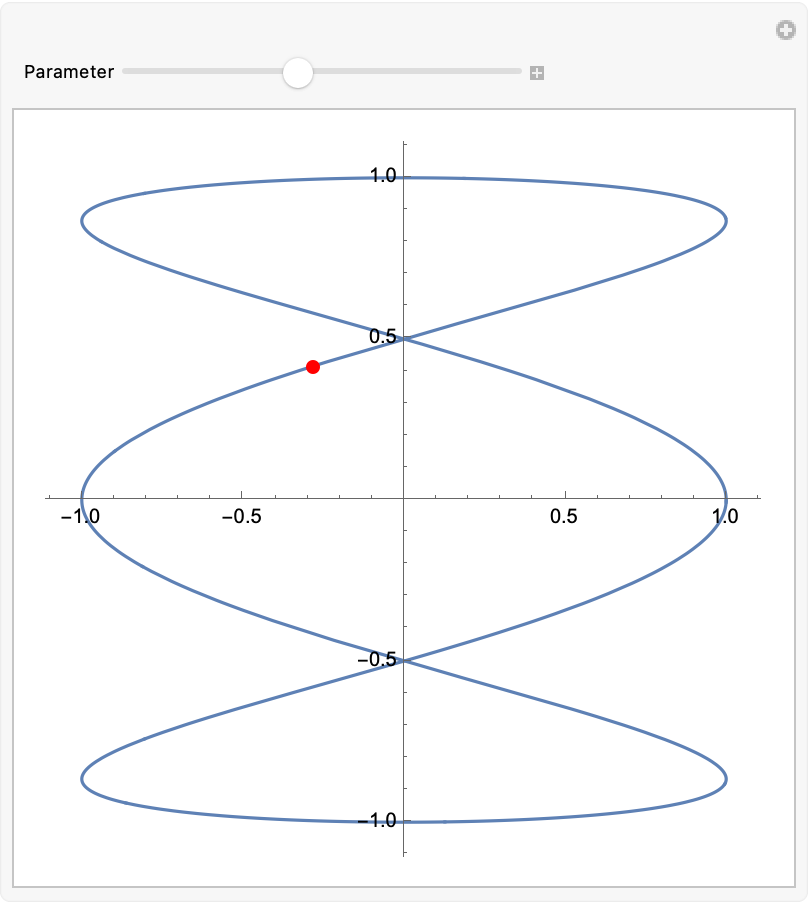

View the motion of two particles moving in the plane colliding at several points:

In[3]:=

$ResourceFunction[ "ManipulateParametricPlot"][{{Cos[t], Sin[t]}, {Cos[3 t], Sin[t]}}, {t, 0, 2 \[Pi], .01}, "DrawVector" -> False, PlotStyle -> {Black, Purple}, "PointStyle" -> {Black, Purple}, ImageSize -> Small, SaveDefinitions -> True]$

Out[3]=

Publisher

Dennis M Schneider

Version History

1.0.0 – 29 July 2022

Related Resources

License Information

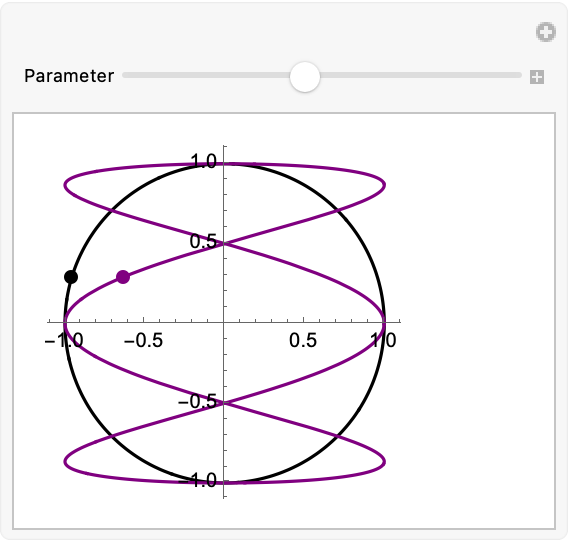This work is licensed under a Creative Commons Attribution 4.0 International License