Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Construct the Malfatti circles of a triangle
ResourceFunction["MalfattiCircles"][{p1,p2,p3}] constructs the Malfatti circles of the triangle with corner points p1,p2, and p3. |
Find the Malfatti circles of a triangle:
| In[1]:= |
| Out[1]= |  |
Show the circles:
| In[2]:= |
| Out[2]= | 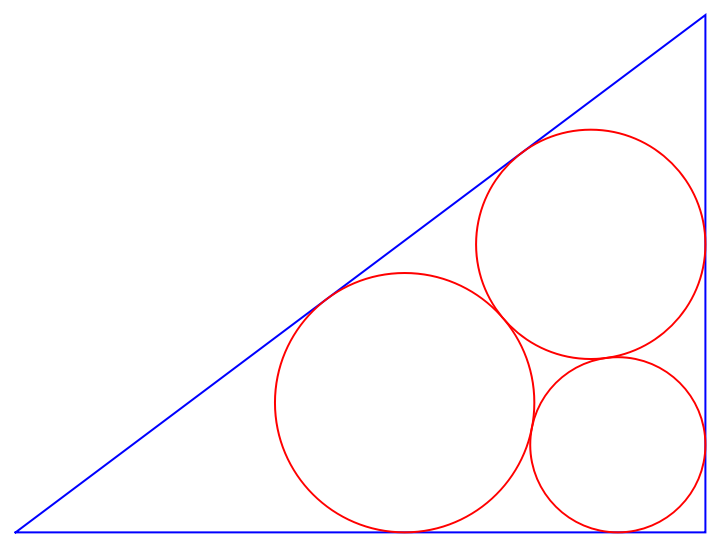 |
Find the Malfatti circles of a Triangle object:
| In[3]:= |
| Out[3]= |  |
Malfatti circles with integer coordinates and radii:
| In[4]:= |
| Out[4]= |
The inradius of a triangle can be expressed in terms of the radii of the Malfatti circles:
| In[5]:= | ![tri = Triangle[{{0, 0}, {4, 0}, {0, 3}}];
rads = Last /@ Simplify[ResourceFunction["MalfattiCircles"][tri]]](https://www.wolframcloud.com/obj/resourcesystem/images/771/771474ad-23dc-48b8-834a-b7803484f6e3/0792c75e582853bf.png) |
| Out[6]= |
| In[7]:= | ![Last[Insphere[tri]] == (2 Sqrt[Apply[Times, rads]])/(
Total[Sqrt[rads]] - Sqrt[Total[rads]]) // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/771/771474ad-23dc-48b8-834a-b7803484f6e3/6b08d464ecbf3107.png) |
| Out[7]= |
Show the Malfatti circles of an arbitrary triangle in a Manipulate:
| In[8]:= | ![Manipulate[
Graphics[{InfiniteLine /@ Subsets[{AA, BB, CC}, {2}], {EdgeForm[Blue], LightBlue, Triangle[{AA, BB, CC}]}, {Red, ResourceFunction["MalfattiCircles"][{AA, BB, CC}]}}, PlotRange -> 6],
{{AA, {1, 3}}, {-4, -4}, {4, 4}, Locator},
{{BB, {-3, -1}}, {-4, -4}, {4, 4}, Locator},
{{CC, {2, -1}}, {-4, -4}, {4, 4}, Locator}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/771/771474ad-23dc-48b8-834a-b7803484f6e3/23adb4181e1cb1d4.png) |
| Out[8]= | 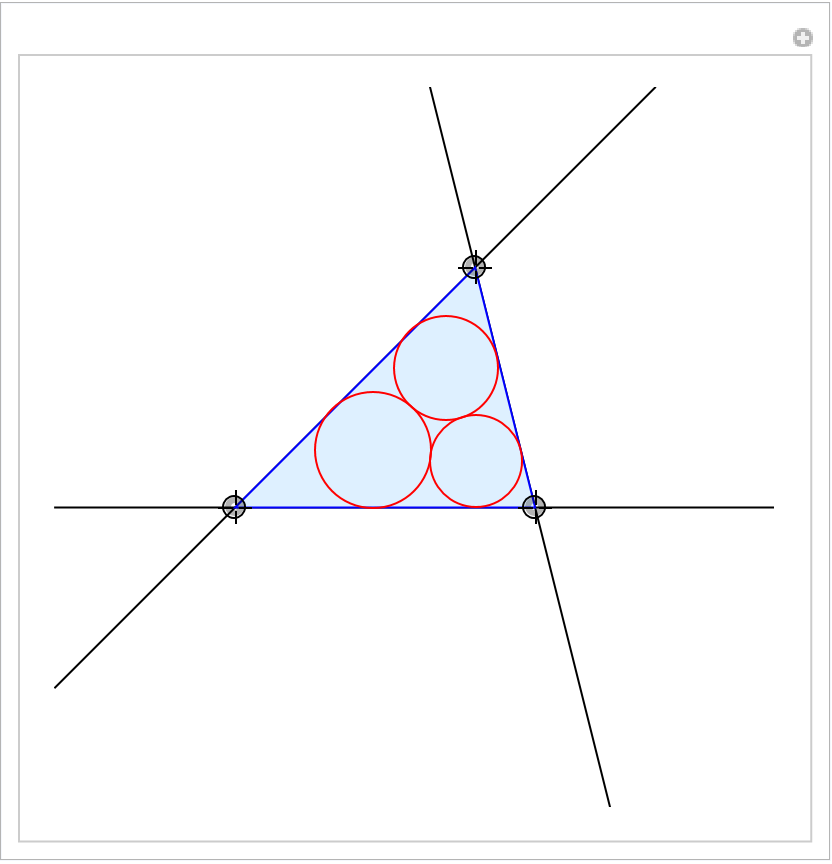 |
Iteratively form the Malfatti circles of the triangle formed by the centers of the excircles:
| In[9]:= | ![NestList[
ResourceFunction["MalfattiCircles"][
First /@ ResourceFunction["Exspheres"][First /@ #]] &, ResourceFunction["MalfattiCircles"][
First /@ ResourceFunction["Exspheres"][Triangle[CirclePoints[3] // N]]], 3] // Graphics](https://www.wolframcloud.com/obj/resourcesystem/images/771/771474ad-23dc-48b8-834a-b7803484f6e3/0b69b3e5f3f2577e.png) |
| Out[9]= | 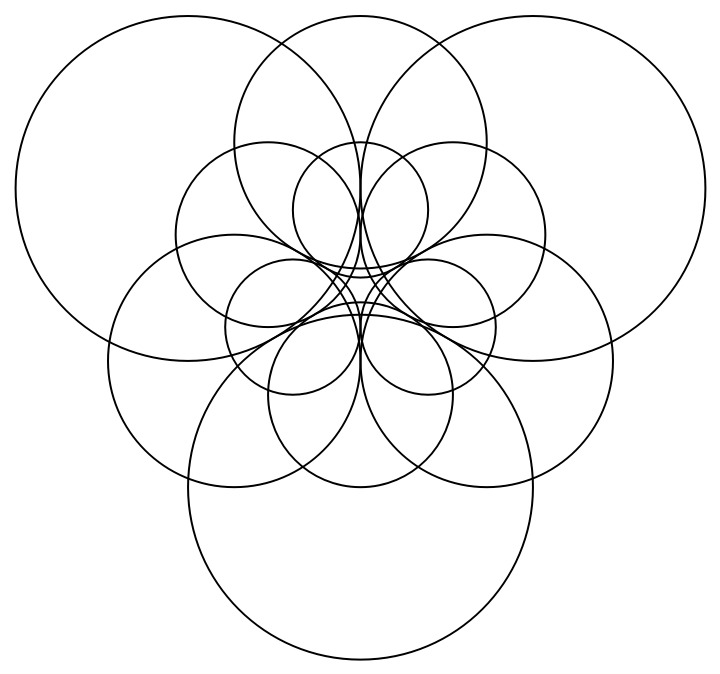 |
This work is licensed under a Creative Commons Attribution 4.0 International License