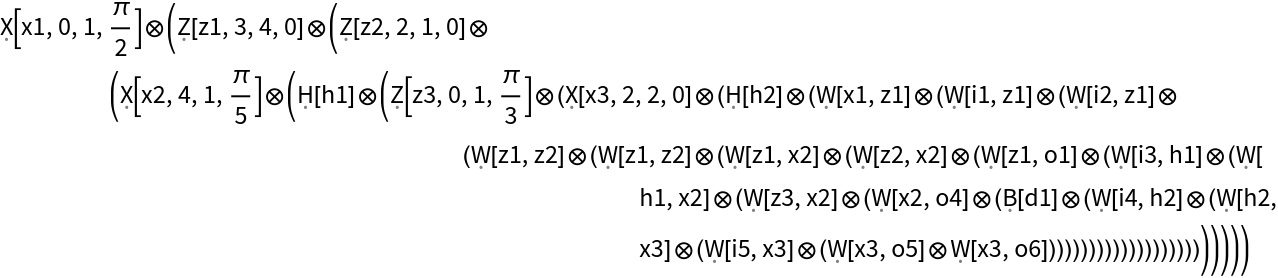Details and Options
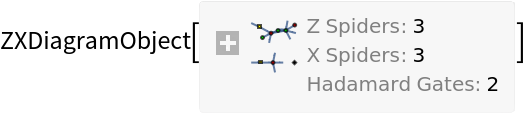
If ResourceFunction["MakeZXDiagram"] succeeds in constructing the specified ZX-diagram, then it returns a ZXDiagramObject expression.
The following generator types are supported:
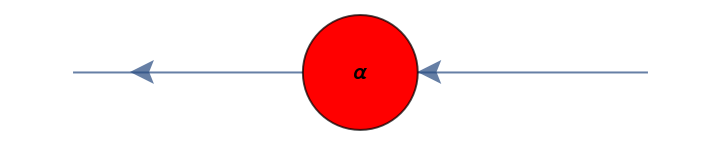
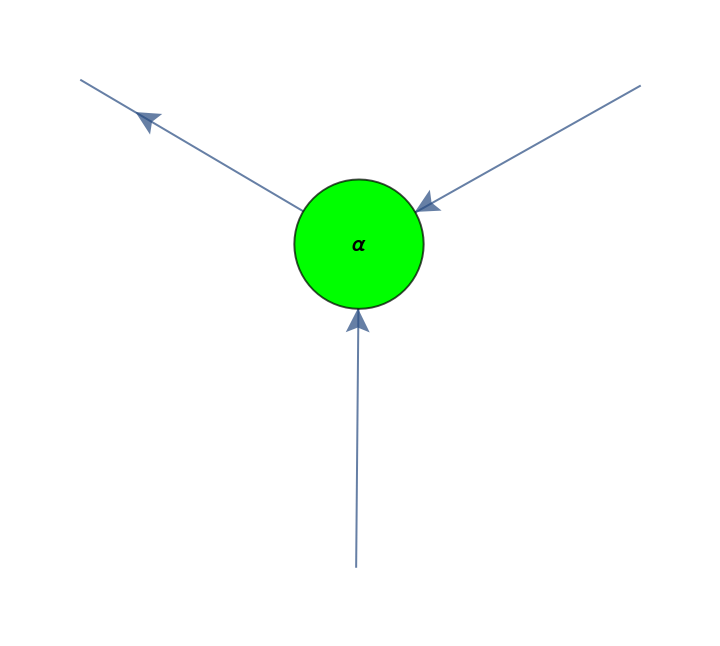
| Z[name,in,out,phase] | a Z-spider with name name, input arity in, output arity out and phase phase |
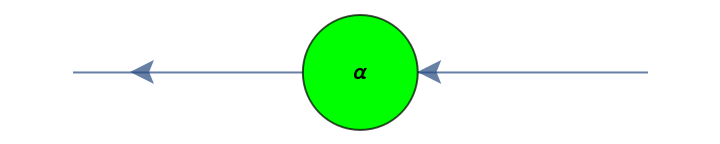
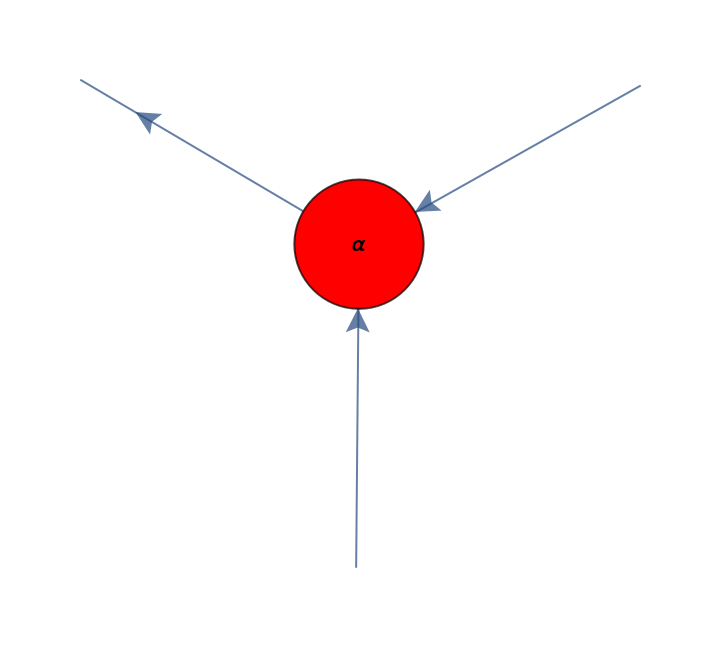
| X[name,in,out,phase] | an X-spider with name name, input arity in, output arity out and phase phase |
| H[name] | a Hadamard gate with name name |
| B[name] | a black diamond with name name |
| W[name1,name2] | a wire connecting generators name1 and name2 |
When specified in
Association form
<|"ZSpiders"→z,"XSpiders"→x,"HadamardGates"→h,"Diamonds"→d,"Wires"→w|>,
z and
x are nested lists of input arities, output arities and phases;
h and
d are integers representing the number of Hadamard gates and black diamonds; and
w is a nested list of generator names connected by wires.
In ZXDiagramObject, the following properties are supported:
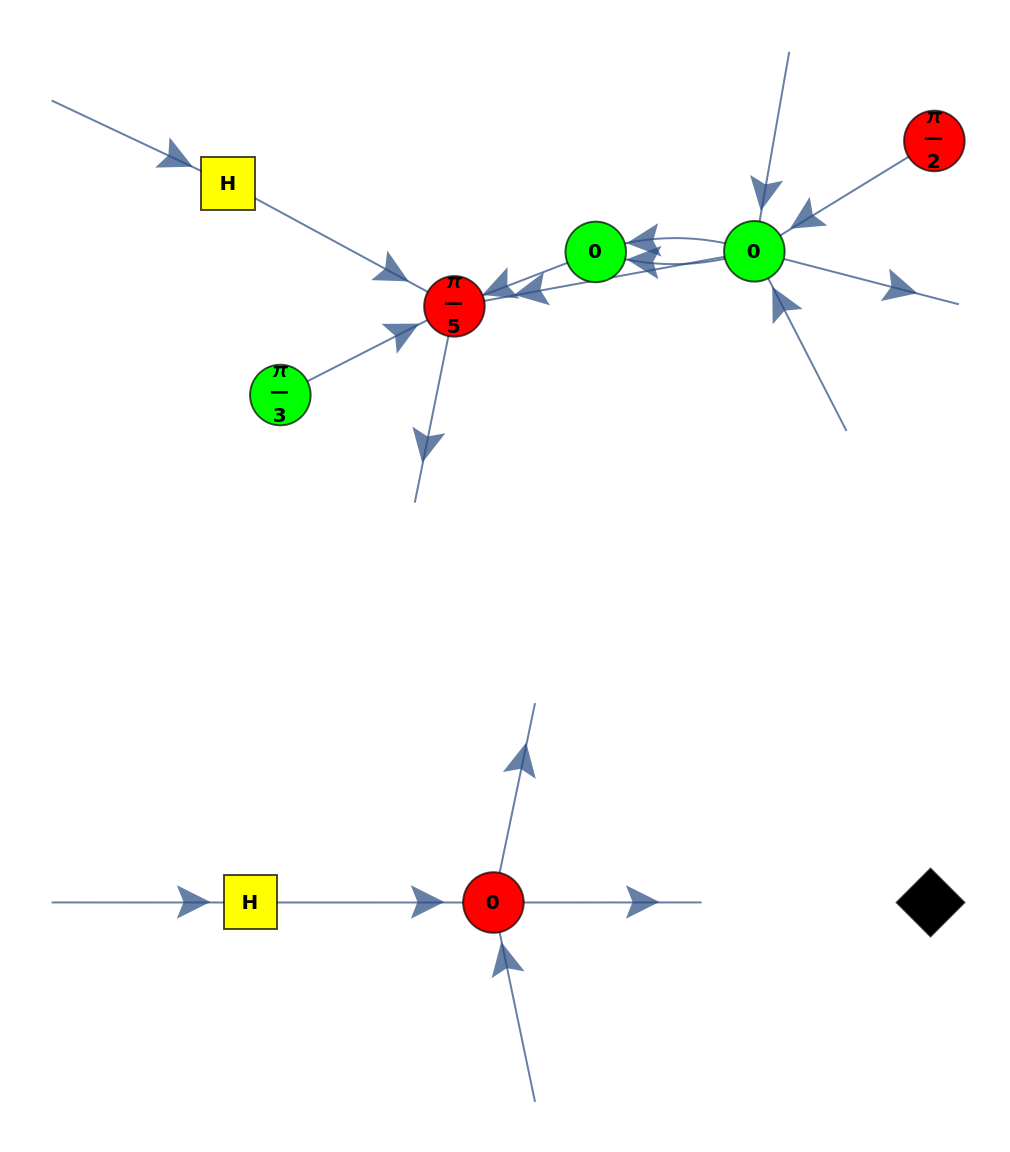
| "LabeledGraph" | graph form of the ZX-diagram with phases labeled |
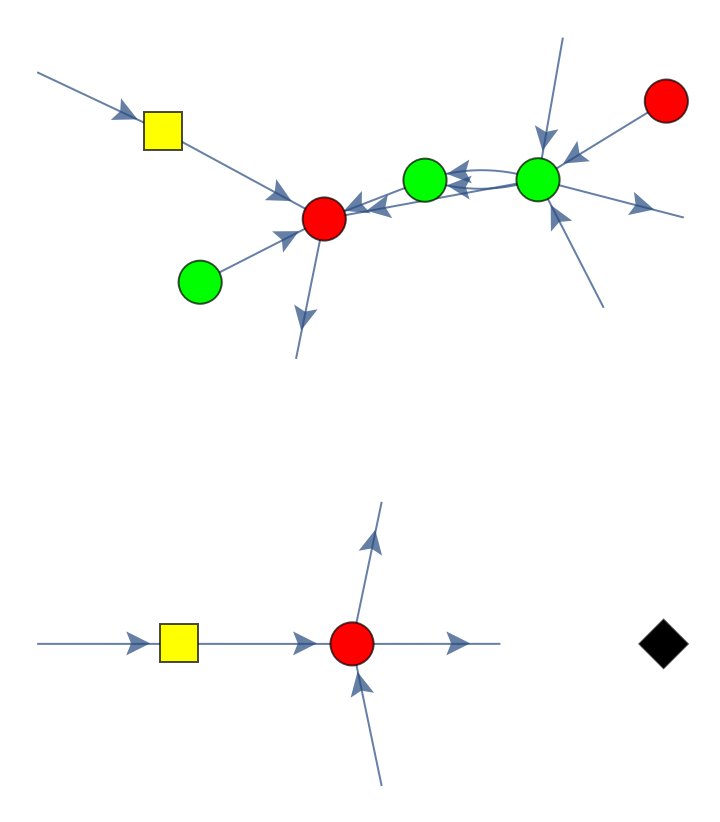
| "UnlabeledGraph" | graph form of the ZX-diagram without phases labeled |
| "OperatorForm" | ZX-diagram represented as a tensor product of generators |
| "ListForm" | ZX-diagram represented as a list of generators |
| "MatrixForm" | ZX-diagram represented as an explicit linear map on qubits |
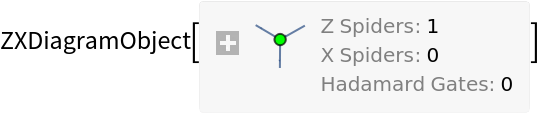
| "ZSpiders" | list of Z-spiders in the ZX-diagram |
| "XSpiders" | list of X-spiders in the ZX-diagram |
| "HadamardGates" | list of Hadamard gates in the ZX-diagram |
| "Diamonds" | list of black diamonds in the ZX-diagram |
| "Wires" | list of wires in the ZX-diagram |
| "ZSpiderCount" | number of Z-spiders in the ZX-diagram |
| "XSpiderCount" | number of X-spiders in the ZX-diagram |
| "HadamardGateCount" | number of Hadamard gates in the ZX-diagram |
| "DiamondCount" | number of black diamonds in the ZX-diagram |
| "WireCount" | number of wires in the ZX-diagram |
The default convention is to name Z-spiders as z1,z2,…; X-spiders as x1,x2,…; Hadamard gates as h1,h2,…; black diamonds as d1,d2,…; inputs as i1,i2,…; and outputs as o1,o2,….

![diagram = ResourceFunction[
"MakeZXDiagram"][<|"ZSpiders" -> {{2, 2}, {1, 1}, {Pi, Pi/2}}, "XSpiders" -> {{1, 1}, {2, 2}, {Pi/3, Pi/4}}, "Wires" -> {{i1, x1}, {i2, x2}, {x1, z1}, {x1, z2}, {x2, z1}, {x2, z2}, {z1, o1}, {z2, o2}}, "HadamardGates" -> 0, "Diamonds" -> 0|>]](https://www.wolframcloud.com/obj/resourcesystem/images/c8c/c8cb4f9d-e7c3-4aeb-910d-dcbeeb3d2535/34e70fcf2edc7d6d.png)
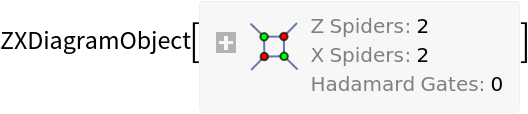
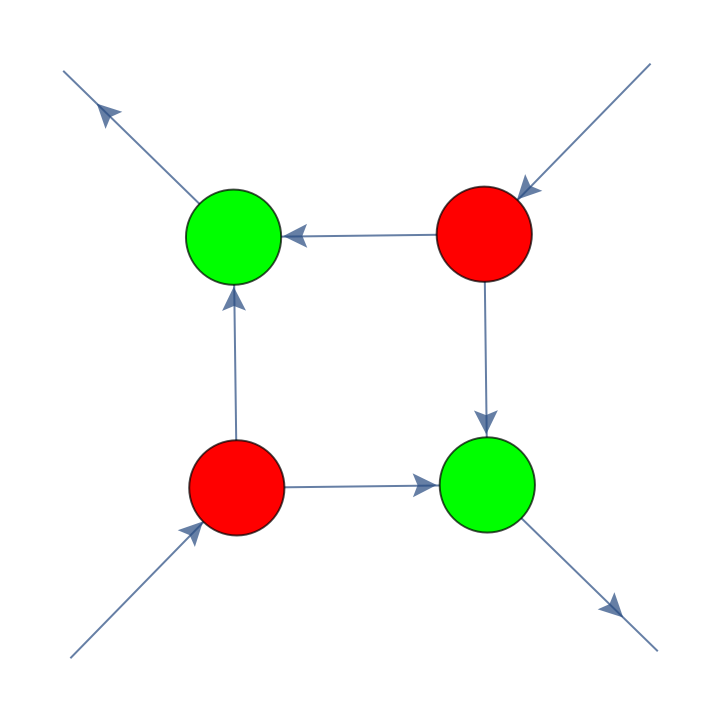
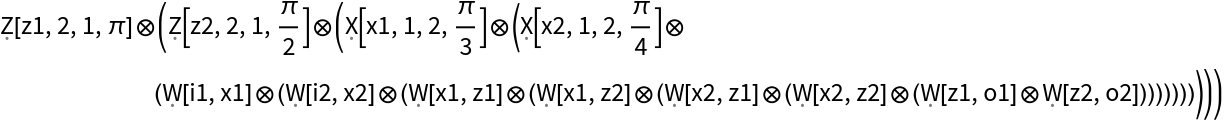
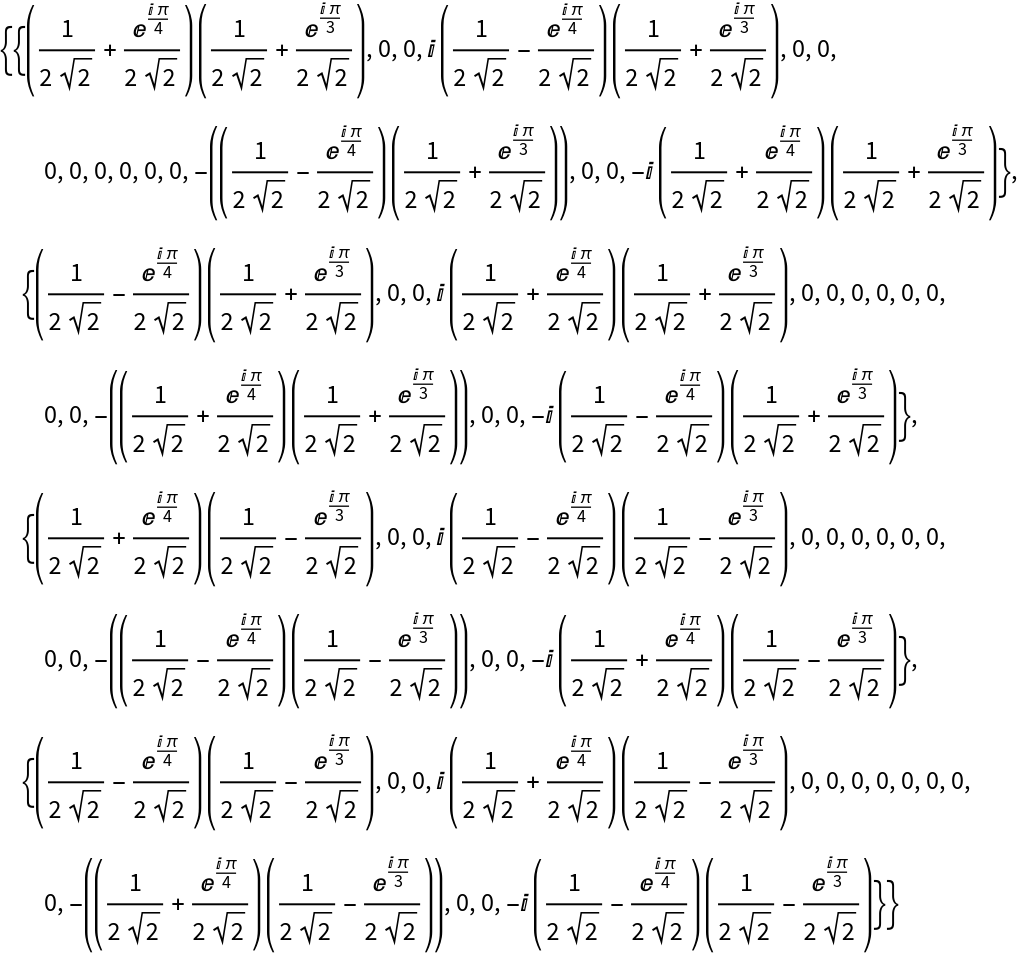
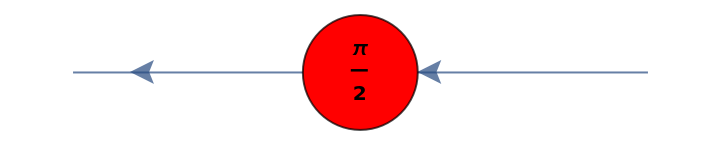
![diagram = ResourceFunction[
"MakeZXDiagram"][{\[FormalCapitalX][x1, 0, 1, Pi/2], \[FormalCapitalZ][z1, 3, 4, 0], \[FormalCapitalZ][z2, 2, 1,
0], \[FormalCapitalX][x2, 4, 1, Pi/5], \[FormalCapitalH][
h1], \[FormalCapitalZ][z3, 0, 1, Pi/3], \[FormalCapitalX][x3, 2, 2, 0], \[FormalCapitalH][h2], \[FormalCapitalW][x1, z1], \[FormalCapitalW][i1, z1], \[FormalCapitalW][i2, z1], \[FormalCapitalW][z1, z2], \[FormalCapitalW][z1, z2], \[FormalCapitalW][z1, x2], \[FormalCapitalW][z2, x2], \[FormalCapitalW][z1, o1], \[FormalCapitalW][i3, h1], \[FormalCapitalW][h1, x2], \[FormalCapitalW][z3, x2], \[FormalCapitalW][x2, o4], \[FormalCapitalB][
d1], \[FormalCapitalW][i4, h2], \[FormalCapitalW][h2, x3], \[FormalCapitalW][i5, x3], \[FormalCapitalW][x3, o5], \[FormalCapitalW][x3, o6]}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8c/c8cb4f9d-e7c3-4aeb-910d-dcbeeb3d2535/4d12cf2c329e2d96.png)
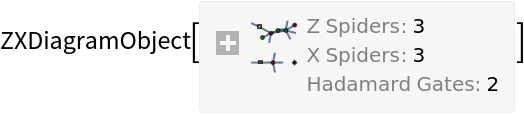
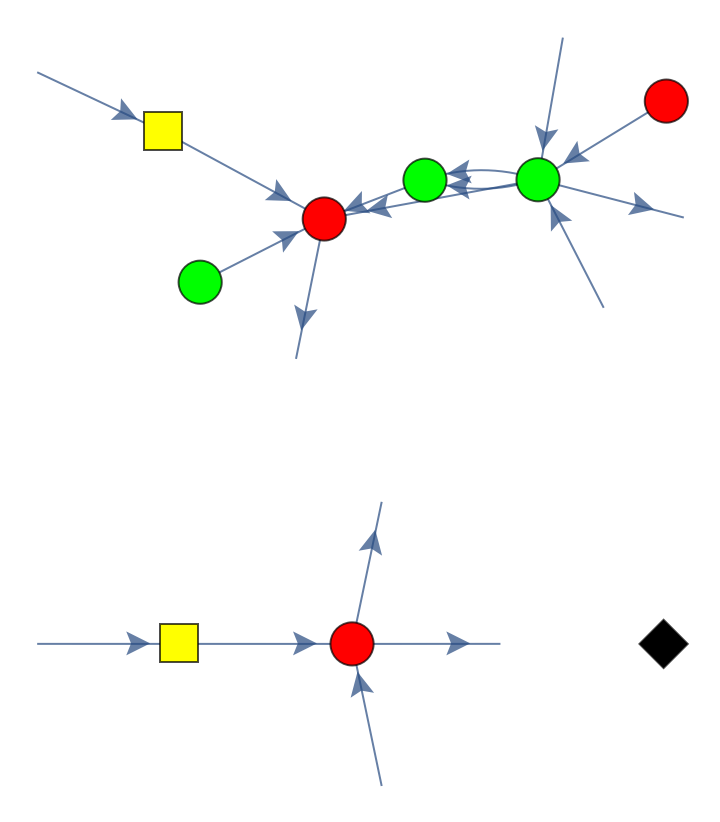
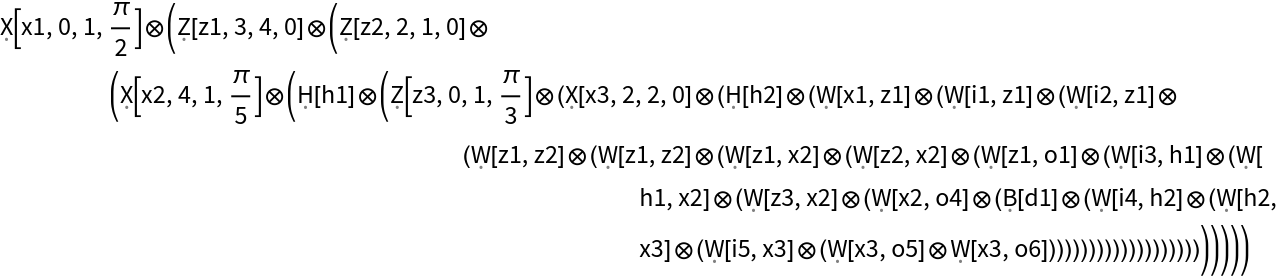







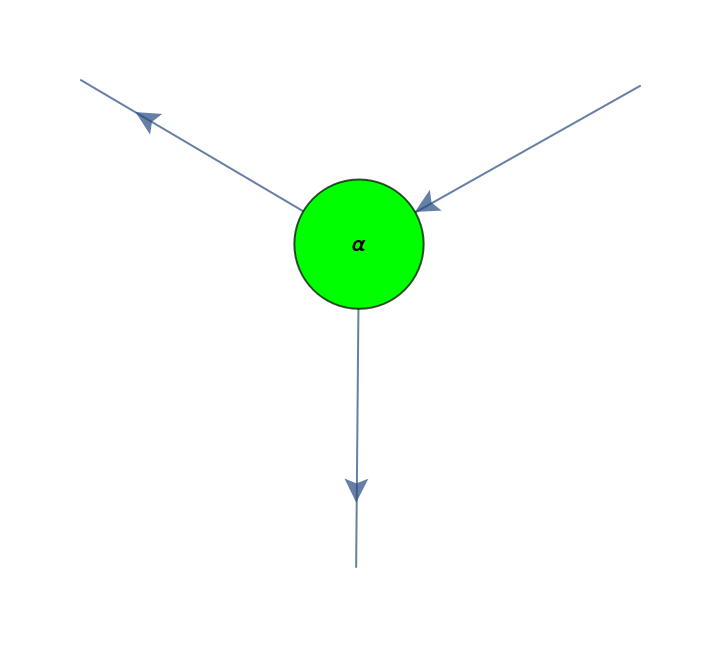
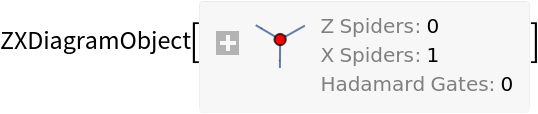
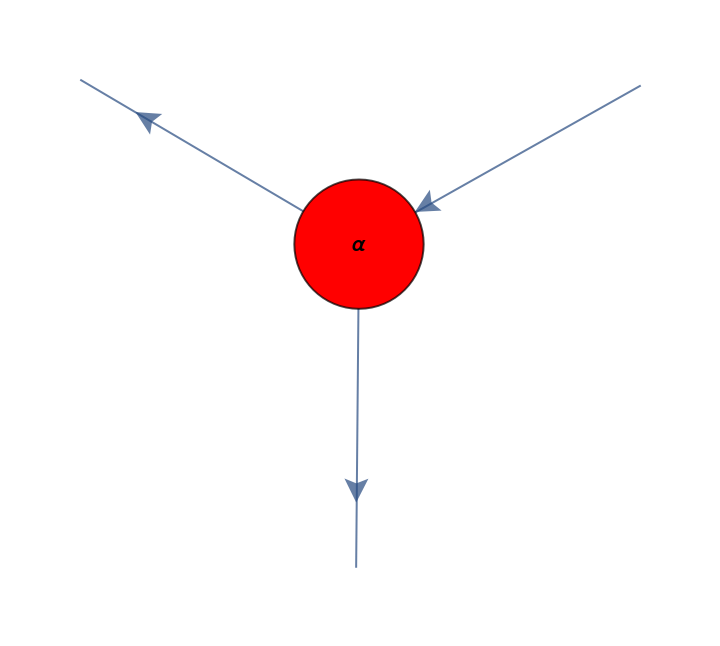
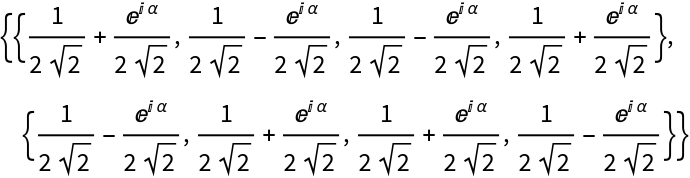
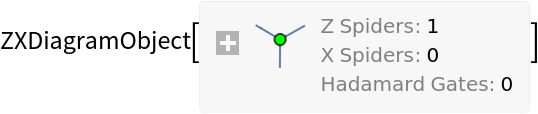
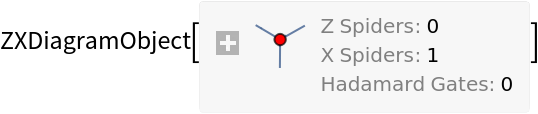
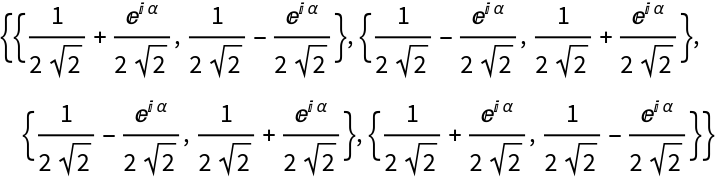





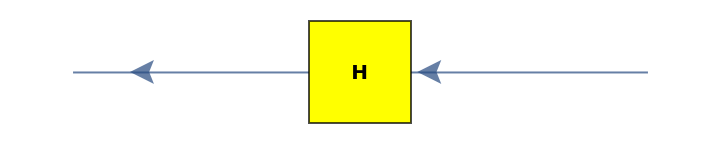


![diagram = ResourceFunction[
"MakeZXDiagram"][{\[FormalCapitalX][x1, 0, 1, Pi/2], \[FormalCapitalZ][z1, 3, 4, 0], \[FormalCapitalZ][z2, 2, 1,
0], \[FormalCapitalX][x2, 4, 1, Pi/5], \[FormalCapitalH][
h1], \[FormalCapitalZ][z3, 0, 1, Pi/3], \[FormalCapitalX][x3, 2, 2, 0], \[FormalCapitalH][h2], \[FormalCapitalW][x1, z1], \[FormalCapitalW][i1, z1], \[FormalCapitalW][i2, z1], \[FormalCapitalW][z1, z2], \[FormalCapitalW][z1, z2], \[FormalCapitalW][z1, x2], \[FormalCapitalW][z2, x2], \[FormalCapitalW][z1, o1], \[FormalCapitalW][i3, h1], \[FormalCapitalW][h1, x2], \[FormalCapitalW][z3, x2], \[FormalCapitalW][x2, o4], \[FormalCapitalB][
d1], \[FormalCapitalW][i4, h2], \[FormalCapitalW][h2, x3], \[FormalCapitalW][i5, x3], \[FormalCapitalW][x3, o5], \[FormalCapitalW][x3, o6]}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8c/c8cb4f9d-e7c3-4aeb-910d-dcbeeb3d2535/1258d42bae30cd89.png)