Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Make an abstract representation of a Petri net configuration
ResourceFunction["MakePetriNet"][p,t,a,init] makes a Petri net using the list of places p, the list of transitions t and the list of arcs a, with initial token distribution init. | |
ResourceFunction["MakePetriNet"][assoc,init] makes a Petri net using the association of places, transitions and arcs assoc, with initial token distribution init. |
| "AssociationForm" | Petri net represented as an association of places, transitions and arcs |
| "Places" | list of places in the Petri net |
| "PlaceCount" | number of places in the Petri net |
| "Transitions" | list of transitions in the Petri net |
| "TransitionCount" | number of transitions in the Petri net |
| "Arcs" | list of arcs in the Petri net |
| "ArcCount" | number of arcs in the Petri net |
| "Tokens" | list of token numbers associated to each place in the Petri net |
| "TokenCount" | total number of tokens across all places in the Petri net |
| "UnlabeledGraph" | directed graph form of the Petri net without token counts represented graphically |
| "LabeledGraph" | directed graph form of the Petri net with token counts represented graphically |
| "WeightedGraph" | directed graph form of the Petri net with token counts represented as vertex weights |
Construct a simple Petri net from lists of four places, three transitions and eight arcs, with an initial distribution of six tokens:
| In[1]:= |
|
| Out[1]= |
|
Show the unlabeled graph:
| In[2]:= |
|
| Out[2]= |
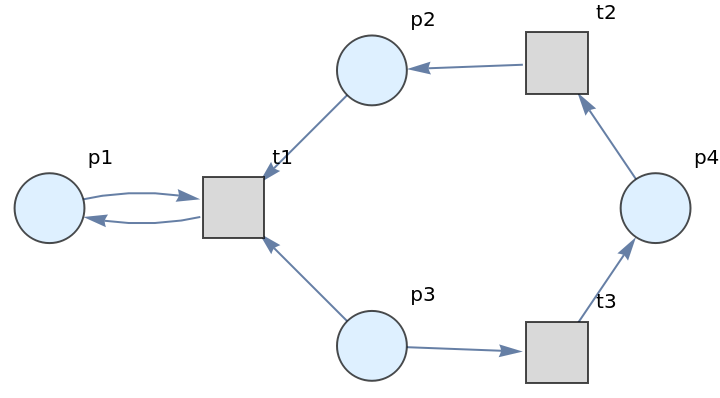
|
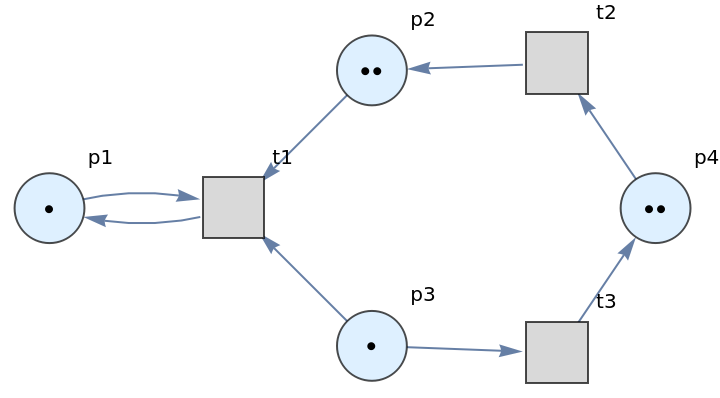
Show the labeled graph with token counts represented graphically:
| In[3]:= |
|
| Out[3]= |
|
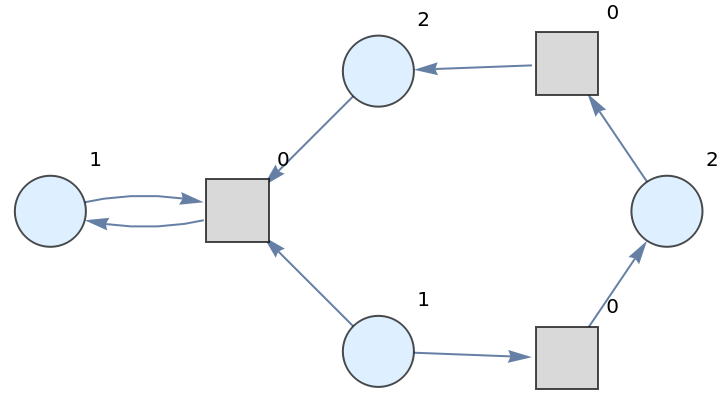
Show the weighted graph with token counts represented as vertex weights:
| In[4]:= |
|
| Out[4]= |
|
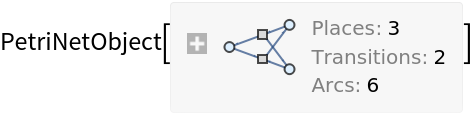
Construct a Petri net representing a simple reversible chemical reaction from an association of three places, two transitions and six arcs, with an initial distribution of twelve tokens:
| In[5]:= |
![petriNet = ResourceFunction[
"MakePetriNet"][<|"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}]](https://www.wolframcloud.com/obj/resourcesystem/images/ef6/ef6061d4-ad20-4930-aadd-3404e99aa95b/19d2064b46a49b2d.png)
|
| Out[5]= |
|
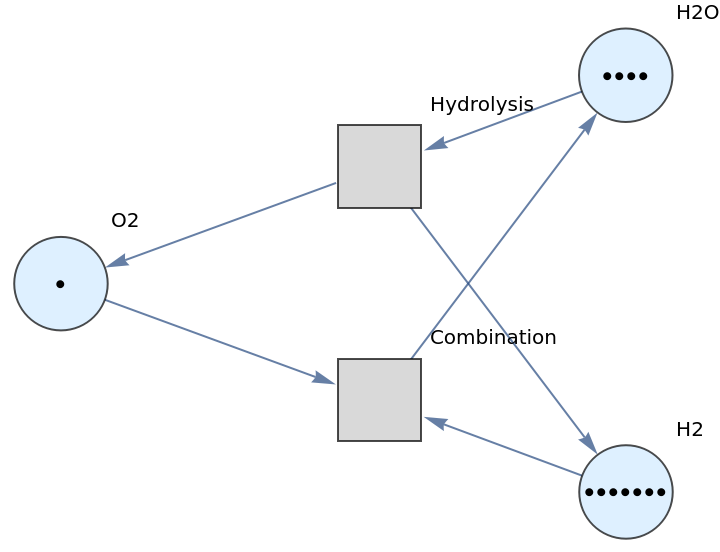
Show the labeled graph with token counts represented graphically:
| In[6]:= |
|
| Out[6]= |
|
Show the association of places, transitions and arcs:
| In[7]:= |
|
| Out[7]= |
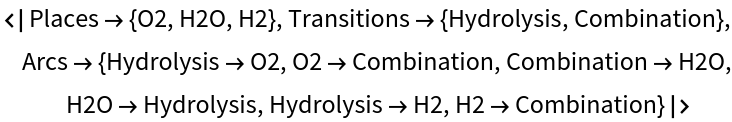
|
Show the list of arcs (directed edges):
| In[8]:= |
|
| Out[8]= |
|
Show the distribution of tokens across places:
| In[9]:= |
|
| Out[9]= |
|
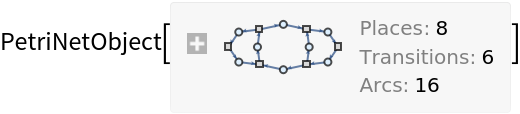
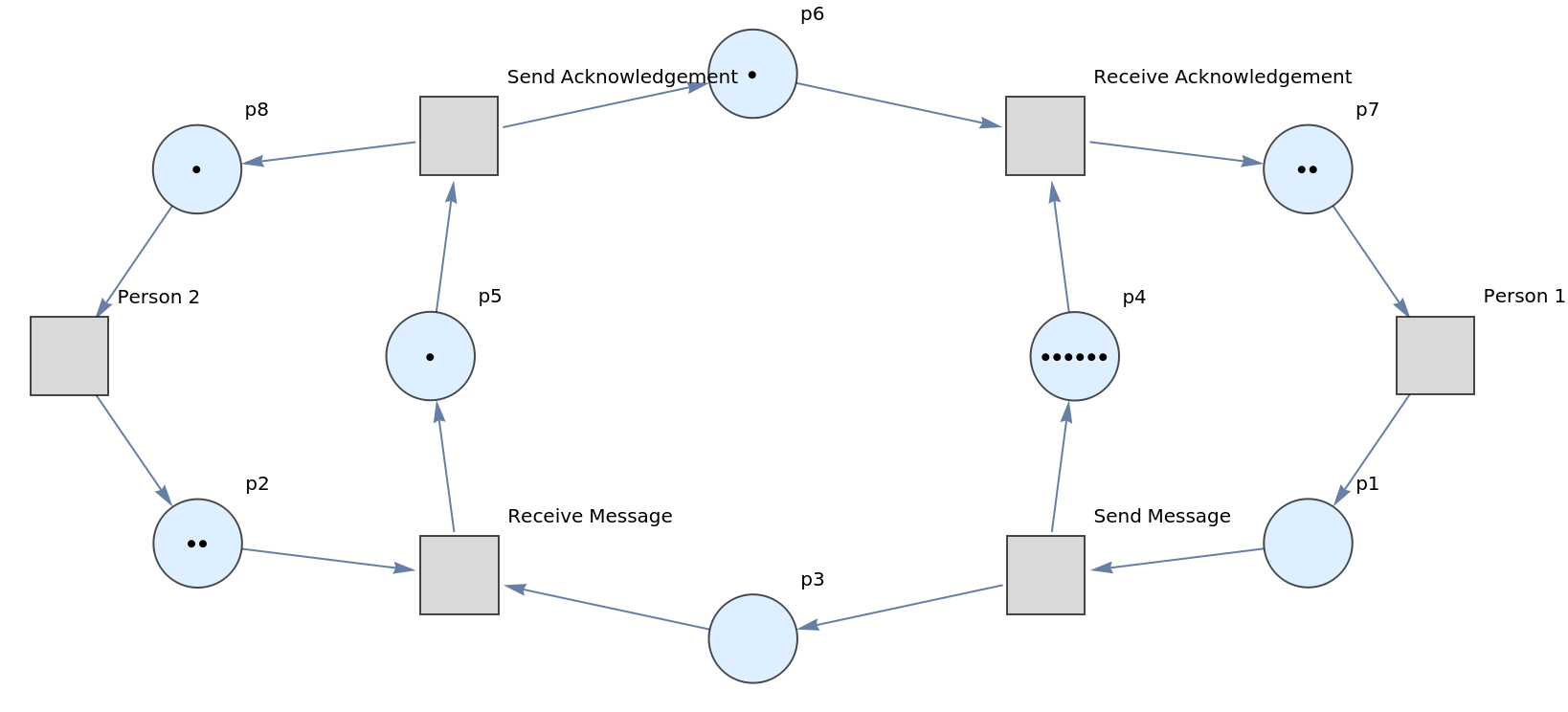
Construct a more complicated Petri net representing a concurrent communications protocol between two agents:
| In[10]:= |
![petriNet = ResourceFunction[
"MakePetriNet"][{p1, p2, p3, p4, p5, p6, p7, p8}, {"Person 1", "Person 2", "Send Message", "Receive Message", "Receive Acknowledgement", "Send Acknowledgement"}, {"Person 1" -> p1, p1 -> "Send Message", "Send Message" -> p3, "Send Message" -> p4, p3 -> "Receive Message", p4 -> "Receive Acknowledgement", "Receive Acknowledgement" -> p7, p7 -> "Person 1", "Receive Message" -> p5, p5 -> "Send Acknowledgement", "Send Acknowledgement" -> p6, "Send Acknowledgement" -> p8, p8 -> "Person 2", "Person 2" -> p2, p2 -> "Receive Message", p6 -> "Receive Acknowledgement"}, {0, 2, 0, 6, 1, 1, 2, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/ef6/ef6061d4-ad20-4930-aadd-3404e99aa95b/048f57e99a065665.png)
|
| Out[10]= |
|
Show the labeled graph with token counts represented graphically:
| In[11]:= |
|
| Out[11]= |
|
Show the list of transitions:
| In[12]:= |
|
| Out[12]= |
|
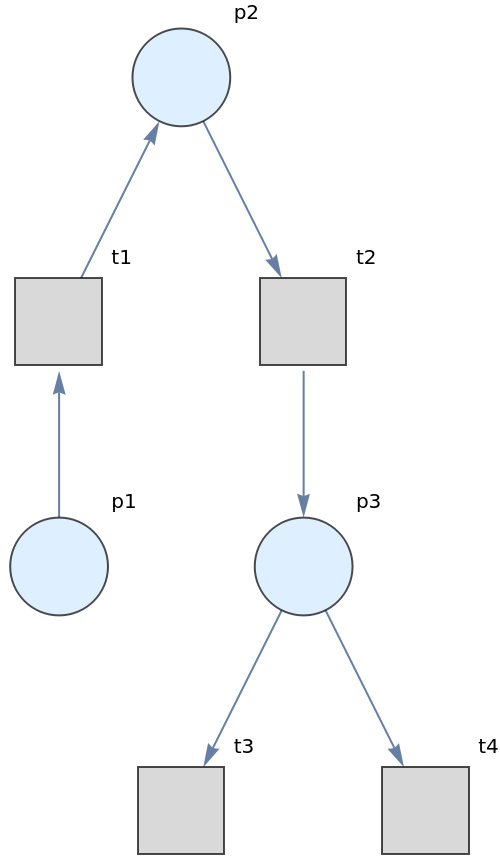
If MakePetriNet is called without an explicit list of token numbers, it is assumed that each place contains no tokens:
| In[13]:= |
|
| Out[13]= |
|
Show the labeled graph:
| In[14]:= |
|
| Out[14]= |
|
Show the default distribution of tokens across places:
| In[15]:= |
|
| Out[15]= |
|
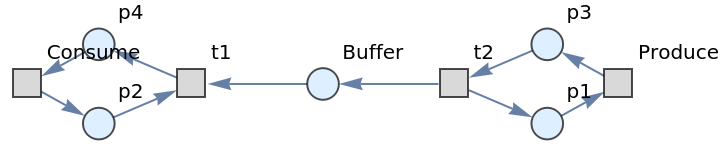
Construct a Petri net representing a simple producer-consumer problem in concurrency theory:
| In[16]:= |
![petriNet = ResourceFunction[
"MakePetriNet"][{p1, p2, p3, "Buffer", p4}, {"Produce", t1, t2, "Consume"}, {p1 -> "Produce", "Produce" -> p3, p3 -> t2, t2 -> p1, t2 -> "Buffer", "Buffer" -> t1, t1 -> p4, p4 -> "Consume", "Consume" -> p2, p2 -> t1}, {1, 3, 0, 6, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/ef6/ef6061d4-ad20-4930-aadd-3404e99aa95b/7ba923d396100af8.png)
|
| Out[16]= |

|
Show the list of properties:
| In[17]:= |
|
| Out[17]= |
|
Show the representation of the Petri net as an association of places, transitions and arcs:
| In[18]:= |
|
| Out[18]= |
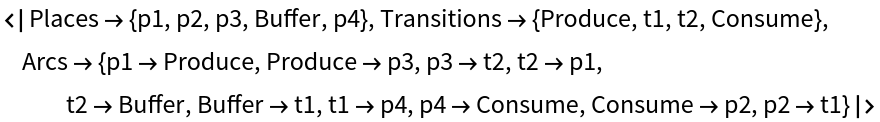
|
Show the list of places in the Petri net:
| In[19]:= |
|
| Out[19]= |
|
Show the number of places in the Petri net:
| In[20]:= |
|
| Out[20]= |
|
Show the list of transitions in the Petri net:
| In[21]:= |
|
| Out[21]= |
|
Show the number of transitions in the Petri net:
| In[22]:= |
|
| Out[22]= |
|
Show the list of arcs in the Petri net:
| In[23]:= |
|
| Out[23]= |
|
Show the number of arcs in the Petri net:
| In[24]:= |
|
| Out[24]= |
|
Show the list of token numbers associated to each place in the Petri net:
| In[25]:= |
|
| Out[25]= |
|
Show the total number of tokens across all places in the Petri net:
| In[26]:= |
|
| Out[26]= |
|
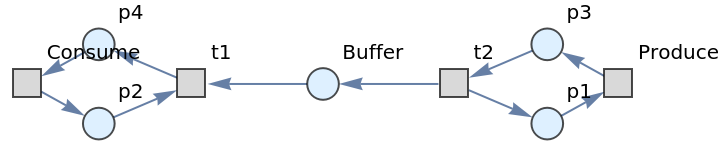
Show the directed graph form of the Petri net without token counts represented graphically:
| In[27]:= |
|
| Out[27]= |
|
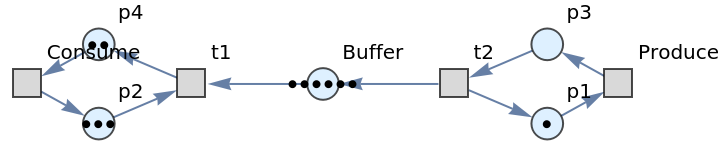
Show the directed graph form of the Petri net with token counts represented graphically:
| In[28]:= |
|
| Out[28]= |
|
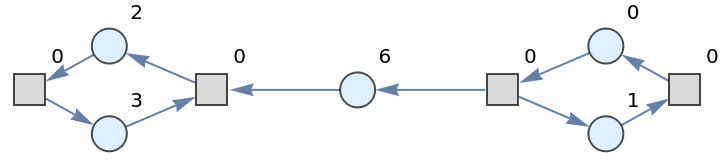
Show the directed graph form of the Petri net with token counts represented as vertex weights:
| In[29]:= |
|
| Out[29]= |
|
| In[30]:= |
|
| Out[30]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License