Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Build an elliptic function with given periods, zeros and poles
ResourceFunction["MakeEllipticFunction"][z,{p1,p2},{r1,…},{s1,…}] builds an elliptic function of complex argument z with periods p1 and p2, zeros ri and poles si. |
Build an elliptic function over a square lattice, with two zeros and two poles:
| In[1]:= |
| Out[1]= | 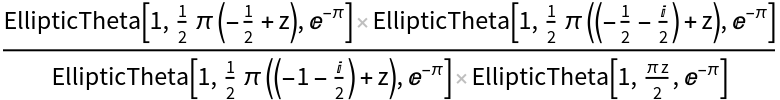 |
Plot the real and imaginary parts of the elliptic function over a subset of the reals:
| In[2]:= |
| Out[2]= | 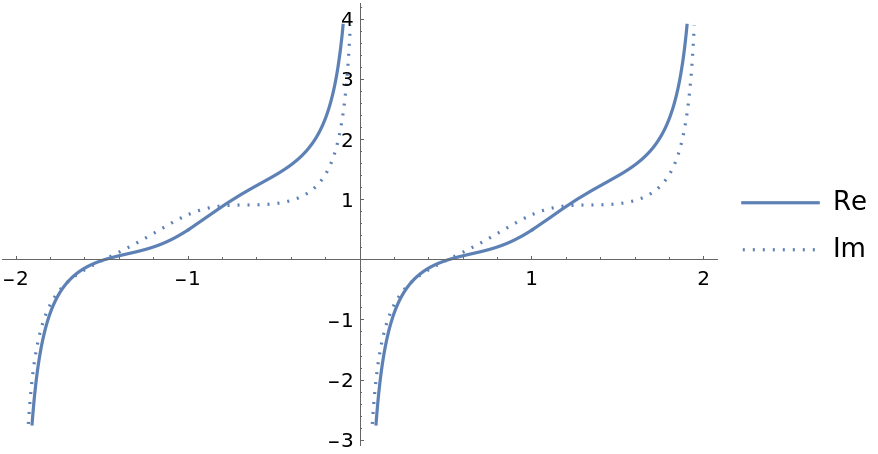 |
Plot the real and imaginary parts of the elliptic function over a subset of the complex plane:
| In[3]:= |
| Out[3]= | 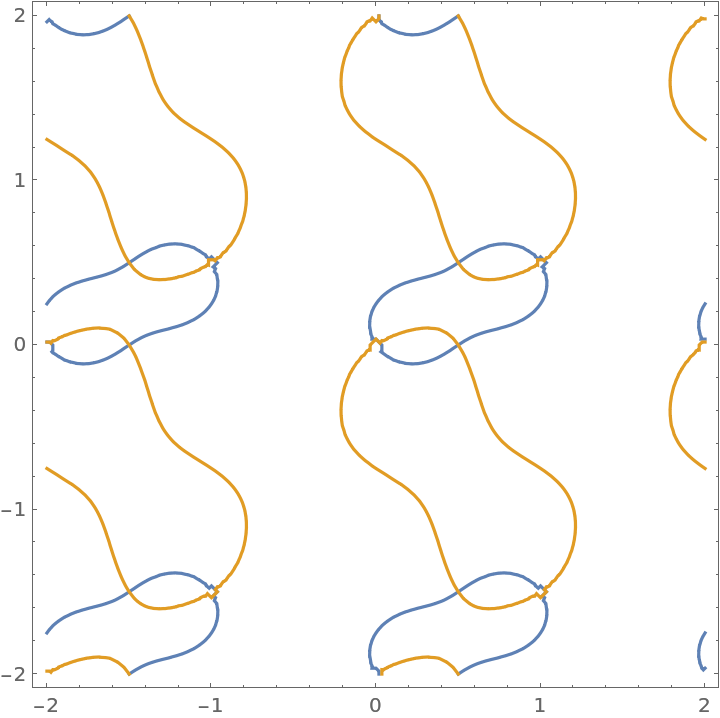 |
Form an elliptic function with a single and a double zero and a triple pole:
| In[4]:= |
| Out[4]= |
Plot over the complex plane:
| In[5]:= |
| Out[5]= | 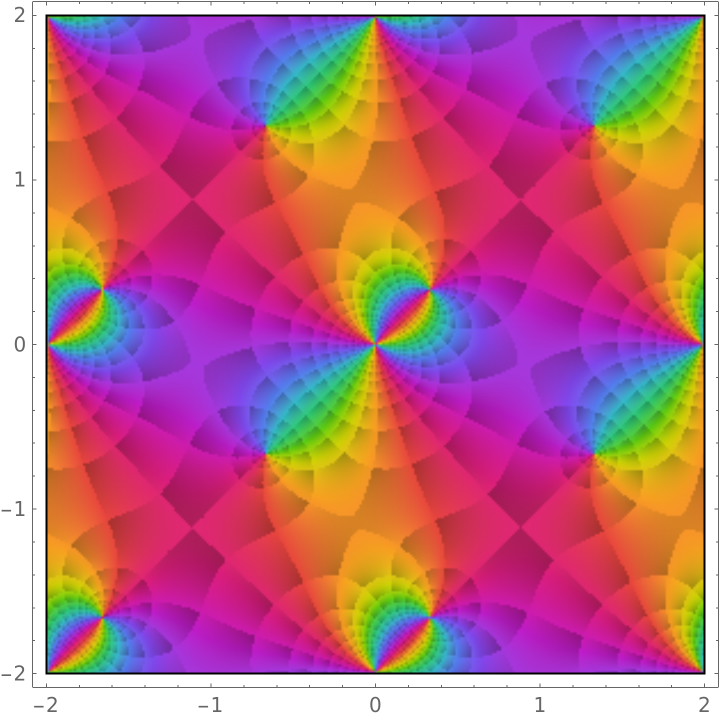 |
Form an elliptic function over the rhomboidal lattice with two triple zeros and one triple pole using the elliptic theta function:
| In[6]:= | ![f1[z_] = ResourceFunction["MakeEllipticFunction"][
z, {2, 1 + I Sqrt[3]}, {0, 0, 0, 2 + (2 I)/Sqrt[3], 2 + (2 I)/Sqrt[3], 2 + (2 I)/Sqrt[3]}, {1, (1 + I Sqrt[3])/2, (3 + I Sqrt[3])/2, 1 + I/Sqrt[3], 1 + I/Sqrt[3], 1 + I/Sqrt[3]}, EllipticTheta] // Quiet](https://www.wolframcloud.com/obj/resourcesystem/images/9b0/9b0a482a-8984-48a0-9798-991605af3987/29570028dae0ae91.png) |
| Out[6]= | 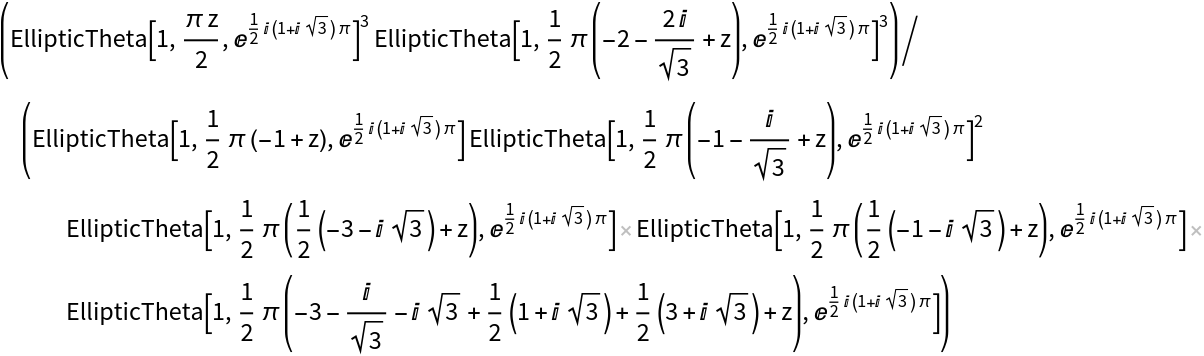 |
Use the Weierstrass sigma function to build the elliptic function:
| In[7]:= | ![f2[z_] = ResourceFunction["MakeEllipticFunction"][
z, {2, 1 + I Sqrt[3]}, {0, 0, 0, 2 + (2 I)/Sqrt[3], 2 + (2 I)/Sqrt[3], 2 + (2 I)/Sqrt[3]}, {1, (1 + I Sqrt[3])/2, (3 + I Sqrt[3])/2, 1 + I/Sqrt[3], 1 + I/Sqrt[3], 1 + I/Sqrt[3]}, WeierstrassSigma] //
Quiet](https://www.wolframcloud.com/obj/resourcesystem/images/9b0/9b0a482a-8984-48a0-9798-991605af3987/0204b9c0a2ed0368.png) |
| Out[7]= |  |
Show both functions in the complex plane:
| In[8]:= |
| Out[8]= | 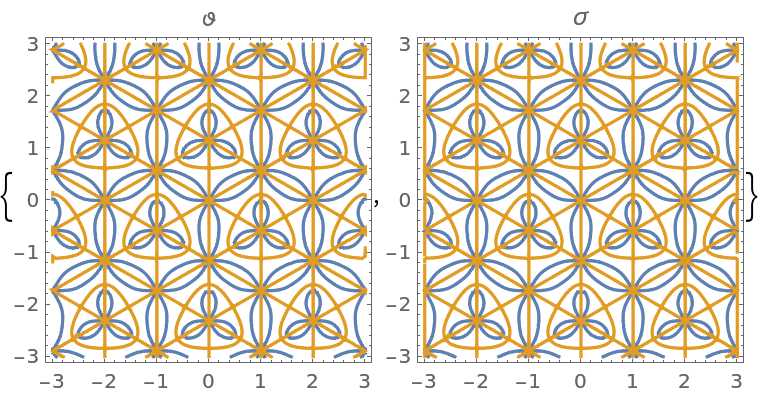 |
The two functions differ by a constant multiple:
| In[9]:= |
| Out[9]= | 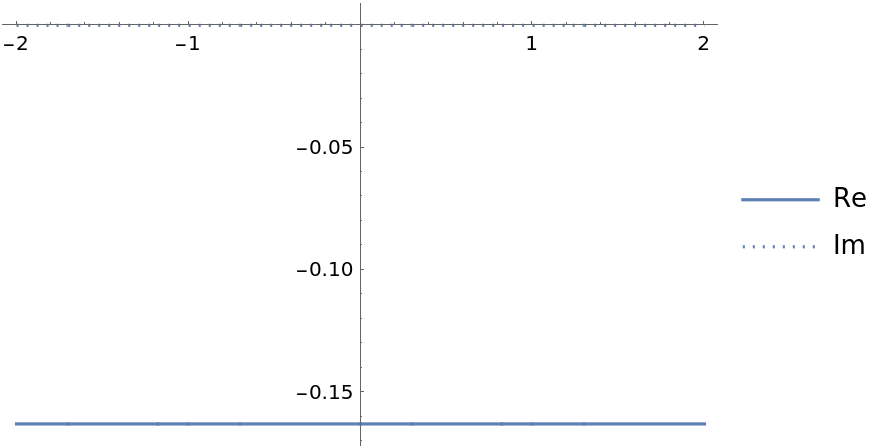 |
| In[10]:= |
| Out[10]= |
MakeEllipticFunction is left unevaluated if it is not possible to build an elliptic function from the specified data:
| In[11]:= |
| Out[11]= |
This work is licensed under a Creative Commons Attribution 4.0 International License