Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get a magic square for any dimension
ResourceFunction["MagicSquare"][n] gives a magic square of dimension n. |
Generate a 6×6 magic square:
| In[2]:= |
| Out[2]= |  |
An 8×8 magic square:
| In[3]:= |
| Out[3]= | 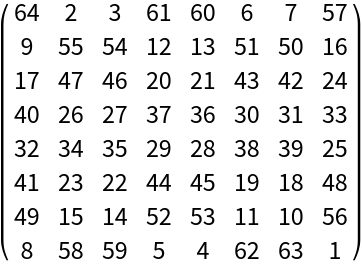 |
Visualize the sums within a 5×5 magic square:
| In[4]:= | ![With[{m = ResourceFunction["MagicSquare"][5], n = 5},
Graphics[{
Table[{Line[{{0, i}, {n, i}}], Line[{{i, 0}, {i, n}}]}, {i, 0, n}],
Table[
Text[Style[ToString[m[[i, j]]], 16], {j - .5, (n - i + 1) - .5}], {i, n}, {j, n}], Red, Table[{Arrow[{{1/2, i - 1/2}, {n - 1/2, i - 1/2}}], Arrow[{{i - 1/2, n - 1/2}, {i - 1/2, 1/2}}]}, {i, n}], Arrow[{{1/2, n - 1/2}, {n - 1/2, 1/2}}], Arrow[{{1/2, 1/2}, {n - 1/2, n - 1/2}}]
}]]](https://www.wolframcloud.com/obj/resourcesystem/images/269/26916a8f-b885-4d63-ae94-b145dfc549d7/4ec743250f0d04ed.png) |
| Out[4]= | 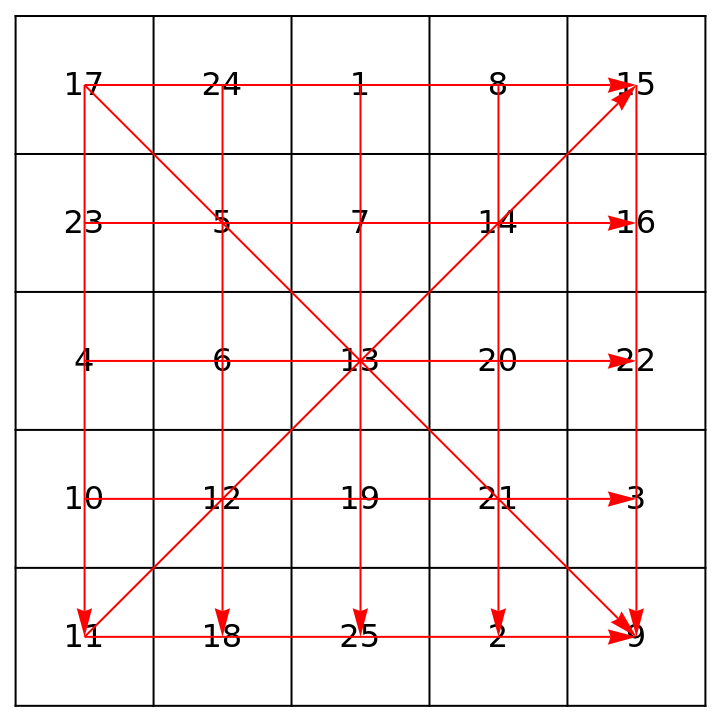 |
Check that the row, column, main diagonal and antidiagonal sums all agree, and are equal to the magic constant:
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License