Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 LuckyNumbers

Source Notebook

Get a list of lucky numbers

Contributed by: Enrique Zeleny

ResourceFunction["LuckyNumbers"][n]

gives the lucky numbers less than or equal to n.

ResourceFunction["LuckyNumbers"][n,k]

gives the lucky numbers less than or equal to n, after iterating the sieving procedure k times.

Details

Lucky numbers are defined through a sieving procedure: start with the odd integers and strike out every third number. This gets rid of 5, 11, 17, 23 and so on. The third surviving number from the left is 7, so strike out every seventh integer not yet eliminated: 19, 39, …. The integers that survive are the lucky numbers.
Lucky numbers seem to share many properties with primes.

Examples

Basic Examples (2) 

Give all the lucky numbers less than 100:

In[1]:=
ResourceFunction["LuckyNumbers"][100]
Out[1]=

Lucky primes are primes that are also lucky numbers:

In[2]:=
If[PrimeQ[#], Style[#, 18], #] & /@ ResourceFunction["LuckyNumbers"][100]
Out[2]=

Scope (2) 

The first 300 integers surviving 6 steps of the sieving process:

In[3]:=
ResourceFunction["LuckyNumbers"][300, 6]
Out[3]=

Number of lucky numbers less than a million:

In[4]:=
Length[ResourceFunction["LuckyNumbers"][1000000]] // Timing
Out[4]=

Applications (1) 

Visualize the sieving procedure for lucky numbers step by step:

In[5]:=
Grid[With[{r = Range[1, 60, 2]}, (ReplacePart[r, Thread[List /@ ( Complement[r, #1]/2 + 1/2) -> ""]] &) /@ Table[ResourceFunction["LuckyNumbers"][65, n], {n, 0, 5}]], Spacings -> .45]
Out[5]=

Neat Examples (5) 

Distance between lucky numbers:

In[6]:=
luckies = ResourceFunction["LuckyNumbers"][1000];
In[7]:=
ListLinePlot[Differences[luckies]]
Out[7]=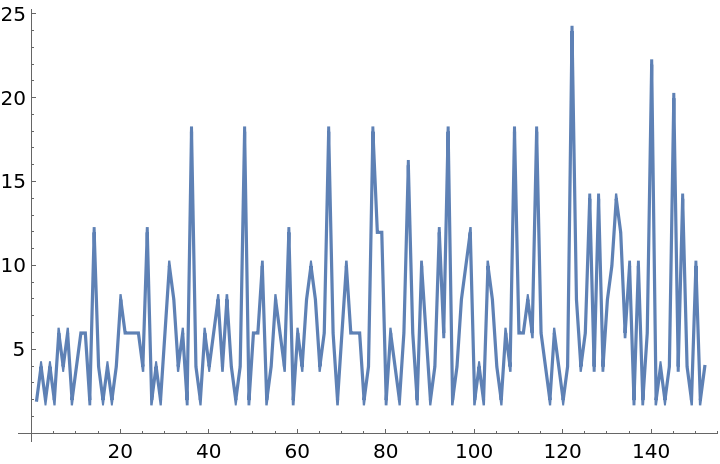

Highlight lucky numbers in an array of integers:

In[8]:=
Grid[Partition[ MapAt[Style[#1, Background -> RGBColor[1, 0.47, 0]] &, Range[500], List /@ TakeWhile[luckies, # < 500 &]], 20], ItemStyle -> {10}]
Out[8]=

Compare lucky numbers with the prime numbers:

In[9]:=
ListLogPlot[{luckies, Table[Prime[k], {k, Length[luckies]}]}, PlotLegends -> {"lucky numbers", "primes"}]
Out[9]=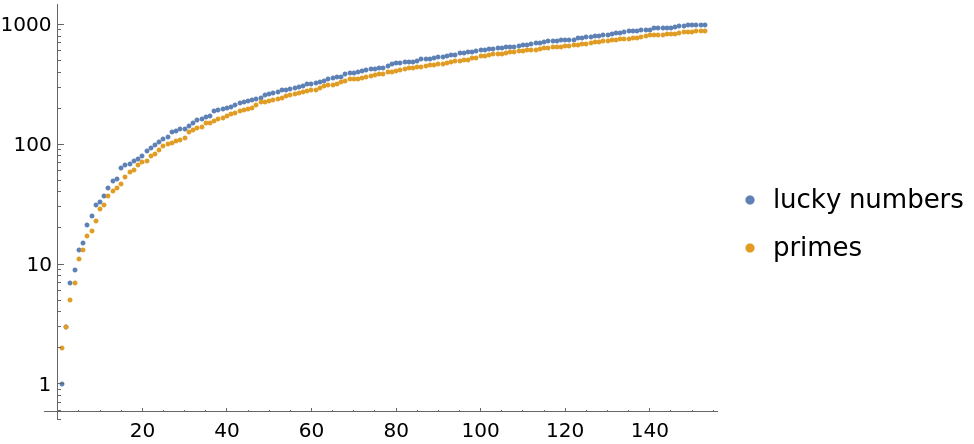

Select "twin" lucky numbers (pairs of lucky numbers that differ by 2):

In[10]:=
Cases[Partition[luckies, 2, 1], {m_, n_} /; n - m == 2]
Out[10]=

Verify a version of the Goldbach conjecture for lucky numbers (an even number is a sum of two lucky numbers) for the first few even numbers:

In[11]:=
Table[Catch[ Table[If[MemberQ[luckies, n - luckies[[i]]], Throw[{n - luckies[[i]], luckies[[i]]}]], {i, 2, 100}]], {n, 4, 100, 2}]
Out[11]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.1.0 – 24 August 2021
  • 1.0.0 – 14 February 2019

Source Metadata

  • Citation:
    • Briggs, W.E., "Prime-like Sequences Generated by a Sieve Process." Duke Mathematical Journal, vol. 30, no. 2, 297-311, 1963. DOI: 10.1215/S0012-7094-63-03032-1
    • Gardiner, V., Lazarus, R., Metropolis, N., Ulam, S., "On certain sequences of integers defined by sieves." Mathematics Magazine, vol. 29, no. 3, 117-122, 1956. DOI: 10.2307/3029719

License Information