Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the lowest common ancestors for pairs of vertices in a graph
ResourceFunction["LowestCommonAncestors"][g,v,w] returns a list of the lowest common ancestors of vertices v and w in a graph g. | |
ResourceFunction["LowestCommonAncestors"][g] returns an Association of lowest common ancestors for each distinct pair of vertices in a graph g. | |
ResourceFunction["LowestCommonAncestors"][g,{{v1,w1},{v2,w2},…}] returns the common ancestors for each vertex pair {vi,wi}. | |
ResourceFunction["LowestCommonAncestors"][g,v] returns lowest common ancestors for a vertex v with all other vertices in a graph g. |
Find a list of lowest common ancestors for a pair of vertices in a graph:
| In[1]:= | ![ResourceFunction["LowestCommonAncestors"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{0, 1, 4, 2, 3}, {{{1, 2}, {1, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 2.}, {0., 1.}}, 0.02261146496815286], ArrowBox[{{0., 2.}, {1., 1.}}, 0.02261146496815286], ArrowBox[{{0., 1.}, {0., 0.}}, 0.02261146496815286], ArrowBox[{{0., 1.}, {1., 0.}}, 0.02261146496815286], ArrowBox[{{1., 1.}, {0., 0.}}, 0.02261146496815286], ArrowBox[{{1., 1.}, {1., 0.}}, 0.02261146496815286]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 2.}, 0.02261146496815286], InsetBox["0", Offset[{2, 2}, {0.02261146496815286, 2.022611464968153}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.02261146496815286], InsetBox["1", Offset[{2, 2}, {0.02261146496815286, 1.0226114649681528}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.02261146496815286], InsetBox["4", Offset[{2, 2}, {1.0226114649681528, 1.0226114649681528}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.02261146496815286], InsetBox["2", Offset[{2, 2}, {0.02261146496815286, 0.02261146496815286}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 0.}, 0.02261146496815286], InsetBox["3", Offset[{2, 2}, {1.0226114649681528, 0.02261146496815286}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{110.79228637069873`, Automatic}]\), 2, 3]](https://www.wolframcloud.com/obj/resourcesystem/images/bbc/bbcc3318-65d5-499b-bd25-0a7a887b4d08/0d2853d72696f43b.png) |
| Out[1]= |
Find all lowest common ancestors for a list of pairs of vertices:
| In[2]:= | ![ResourceFunction["LowestCommonAncestors"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{0, 1, 4, 2, 3}, {{{1, 2}, {1, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 2.}, {0., 1.}}, 0.02261146496815286], ArrowBox[{{0., 2.}, {1., 1.}}, 0.02261146496815286], ArrowBox[{{0., 1.}, {0., 0.}}, 0.02261146496815286], ArrowBox[{{0., 1.}, {1., 0.}}, 0.02261146496815286], ArrowBox[{{1., 1.}, {0., 0.}}, 0.02261146496815286], ArrowBox[{{1., 1.}, {1., 0.}}, 0.02261146496815286]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 2.}, 0.02261146496815286], InsetBox["0", Offset[{2, 2}, {0.02261146496815286, 2.022611464968153}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.02261146496815286], InsetBox["1", Offset[{2, 2}, {0.02261146496815286, 1.0226114649681528}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.02261146496815286], InsetBox["4", Offset[{2, 2}, {1.0226114649681528, 1.0226114649681528}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.02261146496815286], InsetBox["2", Offset[{2, 2}, {0.02261146496815286, 0.02261146496815286}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 0.}, 0.02261146496815286], InsetBox["3", Offset[{2, 2}, {1.0226114649681528, 0.02261146496815286}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{110.79228637069873`, Automatic}]\), {{2, 3}, {1, 4}}]](https://www.wolframcloud.com/obj/resourcesystem/images/bbc/bbcc3318-65d5-499b-bd25-0a7a887b4d08/45b1d837ba580bd7.png) |
| Out[2]= |
Find all lowest common ancestors for all pairs that contain a given vertex:
| In[3]:= | ![ResourceFunction["LowestCommonAncestors"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{0, 1, 4, 2, 3}, {{{1, 2}, {1, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 2.}, {0., 1.}}, 0.02261146496815286], ArrowBox[{{0., 2.}, {1., 1.}}, 0.02261146496815286], ArrowBox[{{0., 1.}, {0., 0.}}, 0.02261146496815286], ArrowBox[{{0., 1.}, {1., 0.}}, 0.02261146496815286], ArrowBox[{{1., 1.}, {0., 0.}}, 0.02261146496815286], ArrowBox[{{1., 1.}, {1., 0.}}, 0.02261146496815286]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 2.}, 0.02261146496815286], InsetBox["0", Offset[{2, 2}, {0.02261146496815286, 2.022611464968153}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.02261146496815286], InsetBox["1", Offset[{2, 2}, {0.02261146496815286, 1.0226114649681528}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.02261146496815286], InsetBox["4", Offset[{2, 2}, {1.0226114649681528, 1.0226114649681528}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.02261146496815286], InsetBox["2", Offset[{2, 2}, {0.02261146496815286, 0.02261146496815286}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 0.}, 0.02261146496815286], InsetBox["3", Offset[{2, 2}, {1.0226114649681528, 0.02261146496815286}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{110.79228637069873`, Automatic}]\), 3]](https://www.wolframcloud.com/obj/resourcesystem/images/bbc/bbcc3318-65d5-499b-bd25-0a7a887b4d08/5e5ac42c73728ea6.png) |
| Out[3]= |
Find all lowest common ancestors for every pair of vertices:
| In[4]:= | ![ResourceFunction["LowestCommonAncestors"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{0, 1, 4, 2, 3}, {{{1, 2}, {1, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 2.}, {0., 1.}}, 0.02261146496815286], ArrowBox[{{0., 2.}, {1., 1.}}, 0.02261146496815286], ArrowBox[{{0., 1.}, {0., 0.}}, 0.02261146496815286], ArrowBox[{{0., 1.}, {1., 0.}}, 0.02261146496815286], ArrowBox[{{1., 1.}, {0., 0.}}, 0.02261146496815286], ArrowBox[{{1., 1.}, {1., 0.}}, 0.02261146496815286]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 2.}, 0.02261146496815286], InsetBox["0", Offset[{2, 2}, {0.02261146496815286, 2.022611464968153}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.02261146496815286], InsetBox["1", Offset[{2, 2}, {0.02261146496815286, 1.0226114649681528}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.02261146496815286], InsetBox["4", Offset[{2, 2}, {1.0226114649681528, 1.0226114649681528}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.02261146496815286], InsetBox["2", Offset[{2, 2}, {0.02261146496815286, 0.02261146496815286}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 0.}, 0.02261146496815286], InsetBox["3", Offset[{2, 2}, {1.0226114649681528, 0.02261146496815286}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{110.79228637069873`, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/bbc/bbcc3318-65d5-499b-bd25-0a7a887b4d08/20b674132d979f40.png) |
| Out[4]= |
| In[5]:= | ![ResourceFunction["LowestCommonAncestors"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {{{2, 1}, {3, 2}, {7, 4}, {7, 5}, {7, 6}, {8, 3}, {8, 7}, {10, 8}, {10, 9}}, Null}, {GraphLayout -> {"LayeredEmbedding", "RootVertex" -> 10, "Orientation" -> Top}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{{0., 0.8164965809277263}, {0., 0.}}, {{0., 1.6329931618554523`}, {0., 0.8164965809277263}}, {{
1.6329931618554523`, 1.6329931618554523`}, {
0.8164965809277261, 0.8164965809277263}}, {{
1.6329931618554523`, 1.6329931618554523`}, {
1.6329931618554523`, 0.8164965809277263}}, {{
1.6329931618554523`, 1.6329931618554523`}, {
2.4494897427831783`, 0.8164965809277263}}, {{
0.8164965809277261, 2.4494897427831783`}, {0., 1.6329931618554523`}}, {{0.8164965809277261, 2.4494897427831783`}, {1.6329931618554523`, 1.6329931618554523`}}, {{1.2247448713915892`, 3.2659863237109046`}, {0.8164965809277261, 2.4494897427831783`}}, {{1.2247448713915892`, 3.2659863237109046`}, {1.6329931618554523`, 2.4494897427831783`}}}, 0.03211708050212858]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 0.}, 0.03211708050212858], InsetBox["1", Offset[{0, -2}, {0., -0.03211708050212858}], ImageScaled[{0.5, 1}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.8164965809277263}, 0.03211708050212858], InsetBox["2", {-0.04496391270298001, 0.8164965809277263}, ImageScaled[{1.25, 0.49999999999999983}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 1.6329931618554523}, 0.03211708050212858], InsetBox["3", {-0.04154123864790748, 1.650200106301193}, ImageScaled[{1.192909649383465, 0.21298742572618223}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.8164965809277261, 0.8164965809277263}, 0.03211708050212858], InsetBox["4", Offset[{0, -2}, {0.8164965809277261, 0.7843795004255977}],
ImageScaled[{0.5, 1}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.6329931618554523, 0.8164965809277263}, 0.03211708050212858], InsetBox["5", Offset[{0, -2}, {1.6329931618554523, 0.7843795004255977}],
ImageScaled[{0.5, 1}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.4494897427831783, 0.8164965809277263}, 0.03211708050212858], InsetBox["6", Offset[{0, -2}, {2.4494897427831783, 0.7843795004255977}],
ImageScaled[{0.5, 1}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.6329931618554523, 1.6329931618554523}, 0.03211708050212858], InsetBox["7", {1.6647874494364094, 1.6647874494364094}, ImageScaled[{-0.030330085889910485, -0.03033008588991093}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.8164965809277261, 2.4494897427831783}, 0.03211708050212858], InsetBox["8", {0.7800199581325175, 2.4757806049793345}, ImageScaled[{1.1084316388816706, 0.061467286502176144}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.6329931618554523, 2.4494897427831783}, 0.03211708050212858], InsetBox["9", Offset[{0, -2}, {1.6329931618554523, 2.41737266228105}], ImageScaled[{0.5, 1}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.2247448713915892, 3.2659863237109046}, 0.03211708050212858], InsetBox["10", Offset[{0, 2}, {1.2247448713915892, 3.298103404213033}], ImageScaled[{0.5, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageMargins->0.,
ImageSize->{285.0077714461818, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/bbc/bbcc3318-65d5-499b-bd25-0a7a887b4d08/4f93c6a512a3f6c7.png) |
| Out[5]= | 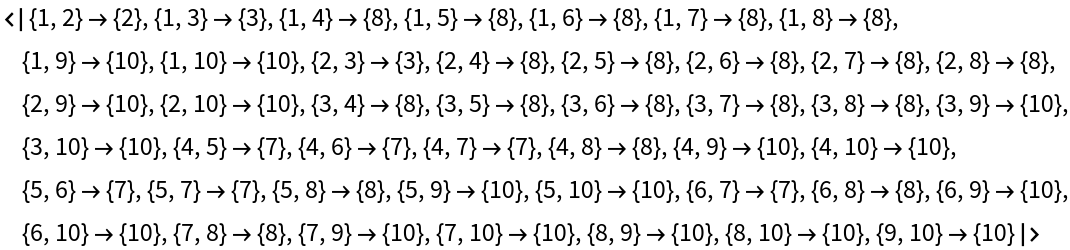 |
Measure an average time and spatial distance between pairs of events in a causal graph using longest distance to their lowest common ancestor:
| In[6]:= | ![With[{causalGraph = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {
SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 0, 0, 0, 3, 4, 8, 9, 11, 15, 15}, {{5}, {6}, {
7}, {10}, {1}, {2}, {3}, {10}, {1}, {5}, {6}, {2}, {
3}, {7}, {10}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexLabels -> {Automatic}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{-2., 3.}, {-1., 2.}}, 0.03700564971751412], ArrowBox[{{-2., 3.}, {-2., 2.}}, 0.03700564971751412], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQDQUHIBSHw0W3D3fDTjMcmH6HfWLILHaHZpbQbS4H
GQ/sr726JFae3UHCUq/z5EOmA6WPM6yl+9kcep5Uhz3VYTmwm/dQSO9LVodH
bHZyMxaxHuj/8+DDZj1WB4kFJQ8eOrEf+LL+KH9/HIuDwQb5uYd4OQ+8UC/Y
KFfJ7KBlbh9ixcx9ICflwdWkOiYHFtPLrJ7KvAfqUsVqo/MYHU4k+c0R2Mt7
YFmFw7wocUaHhcxrth9w4TsQvOxEqPZWBodJ4m/CI3fxHeh4t27xWXcGh2nz
+GpvyfIfaF30jL953n/7TTOE1V3y+Q9wzNVm5Zv+z/4J6+/Qaev4D8w6o6Nu
U/nXXufZEc6Lt/kPmBu+KuV1/WPfY1no9OUb/4FHp5I/Nv76ZQ8JF4EDs2aC
wE84//yNo6/nm/+A8z8fVkp98PKbPSOUzx69gTV6w1e4PPu8vLP83V/g/K89
sXv+VX6G8y+p1wLRJzgfrHzKRzg/ItGvROPABzgfQn+wBwCPCq1F
"]], 0.03700564971751412], ArrowBox[{{-1., 2.}, {-1., 1.}}, 0.03700564971751412], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQDQUHoLRDbJG8S1Dmv/16O/mVVpr8t//xLXRyWe2f
/bW/V3nutvtnf7l38dscm1/7Xx27WGYm99f+hRlHsOmy7/tLpVtWSl3+bW/3
qfnw+V1f9sv9PPgwPfaX/fn9YvY2VR/3v4jvlpfb+8Pezr6x++uJ1/sv+D9I
sv30zT5amXm92OfH+6+fOLD66J8v9g/D0y5uf3pt/59TOr+23flkf+Jlj2y1
+KX9Xh8bbLbqfbL/fdS+9cvm0/uX+0xcHZb10Z6p3a4xK+rIfoG7se6z+z/Y
e+rqxG1w2bOf2/WsPJvte6j+TfuFrMK5ZPTeQtUv2W80M9Kv4tMrqPyk/XlJ
V15Ldb2wPwPmF+0/MvX4I+avT+1hAWQMBo/h/Hkbu6/b5z+A88/xd09pXH4b
zhfPOSiWc/AanC9ZscvUXucSnL8i/c2jr+dPw/lT7F5Otnt5GM5/8PLanw0e
O+H8f1pnOvlYV8D5MAAAIRW7qg==
"]], 0.03700564971751412], ArrowBox[{{-2., 2.}, {-3., 1.}}, 0.03700564971751412], ArrowBox[{{-2., 2.}, {-2., 1.}}, 0.03700564971751412], ArrowBox[{{-2., 2.}, {-1., 1.}}, 0.03700564971751412], ArrowBox[{{-4., 1.}, {0., 0.}}, 0.03700564971751412], ArrowBox[{{-1., 3.}, {-1., 2.}}, 0.03700564971751412], ArrowBox[{{-1., 3.}, {-2., 2.}}, 0.03700564971751412], ArrowBox[{{-3., 2.}, {-3., 1.}}, 0.03700564971751412], ArrowBox[{{-3., 2.}, {-2., 1.}}, 0.03700564971751412], ArrowBox[{{-3., 2.}, {-4., 1.}}, 0.03700564971751412], ArrowBox[{{-3., 2.}, {-1., 1.}}, 0.03700564971751412]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[
1]}], {DiskBox[{0., 0.}, 0.03700564971751412], InsetBox["1", Offset[{2, 2}, {0.03700564971751412, 0.03700564971751412}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-3., 1.}, 0.03700564971751412], InsetBox["2", Offset[{2, 2}, {-2.962994350282486, 1.0370056497175142}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-2., 1.}, 0.03700564971751412], InsetBox["3", Offset[{2, 2}, {-1.9629943502824858, 1.0370056497175142}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-2., 3.}, 0.03700564971751412], InsetBox["4", Offset[{2, 2}, {-1.9629943502824858, 3.037005649717514}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 2.}, 0.03700564971751412], InsetBox["5", Offset[{2, 2}, {-0.9629943502824859, 2.037005649717514}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-2., 2.}, 0.03700564971751412], InsetBox["6", Offset[{2, 2}, {-1.9629943502824858, 2.037005649717514}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-4., 1.}, 0.03700564971751412], InsetBox["7", Offset[{2, 2}, {-3.962994350282486, 1.0370056497175142}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 3.}, 0.03700564971751412], InsetBox["8", Offset[{2, 2}, {-0.9629943502824859, 3.037005649717514}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-3., 2.}, 0.03700564971751412], InsetBox["9", Offset[{2, 2}, {-2.962994350282486, 2.037005649717514}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 1.}, 0.03700564971751412], InsetBox["10", Offset[{2, 2}, {-0.9629943502824859, 1.0370056497175142}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{226.421875, Automatic}]\)},
Association@KeyValueMap[
#1 -> Mean@({Subtract[##], Plus[##]} & @@@ Table[Length@
ResourceFunction["FindLongestPath"][causalGraph, from, to] - 1, {from, #2}, {to, #1}]) &,
DeleteCases[
ResourceFunction["LowestCommonAncestors"][causalGraph], {}]
]
]](https://www.wolframcloud.com/obj/resourcesystem/images/bbc/bbcc3318-65d5-499b-bd25-0a7a887b4d08/5183b5da49c97348.png) |
| Out[6]= | 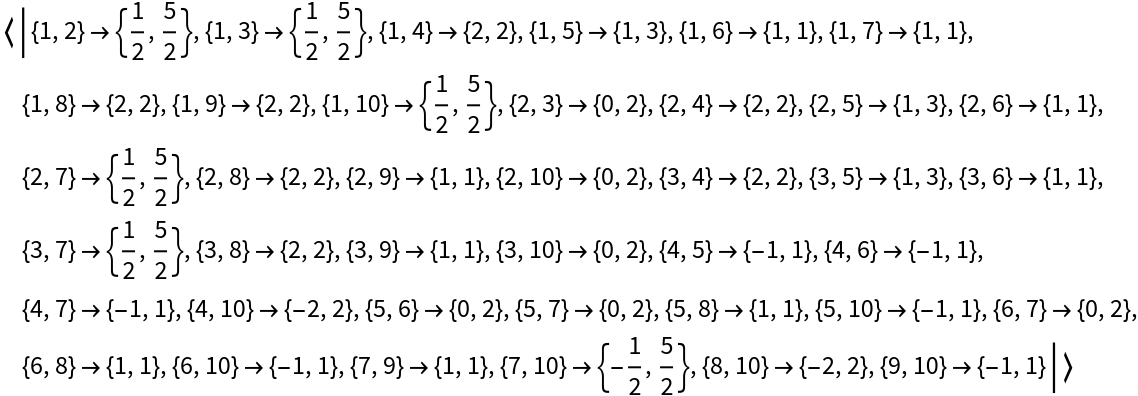 |
This work is licensed under a Creative Commons Attribution 4.0 International License