Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 LollipopGraph

Source Notebook

Return a lollipop graph composed of a clique and a path graph

Contributed by: Alejandra Ortiz Duran

ResourceFunction["LollipopGraph"][n,m]

gives a lollipop graph composed of a clique of size n and a undirected path graph of size m.

Details and Options

LollipopGraph[n,m] is a undirected graph consisting of a n-complete graph connected to a path graph of length m.
ResourceFunction["LollipopGraph"] generates a Graph object.
ResourceFunction["LollipopGraph"] gives a undirected graph with m+n vertices and (n(n-1))/2+m edges.
ResourceFunction["LollipopGraph"] takes the same options as Graph.

Examples

Basic Examples

In[1]:=
ResourceFunction["LollipopGraph"][5, 3]
Out[1]=

Options (12) 

AnnotationRules (2) 

Specify an annotation for vertices:

In[2]:=
ResourceFunction["LollipopGraph"][5, 3, AnnotationRules -> {1 -> {VertexLabels -> "hello"}}]
Out[2]=

Edges:

In[3]:=
ResourceFunction["LollipopGraph"][5, 3, EdgeLabels -> {5 \[UndirectedEdge] 6 -> "hello"}]
Out[3]=

GraphHighlight (3) 

Highlight the vertex 1:

In[4]:=
ResourceFunction["LollipopGraph"][5, 3, GraphHighlight -> {5}, ImageSize -> Medium]
Out[4]=

Highlight the edge 23:

In[5]:=
ResourceFunction["LollipopGraph"][5, 3, GraphHighlight -> {5 \[UndirectedEdge] 6}, ImageSize -> Medium]
Out[5]=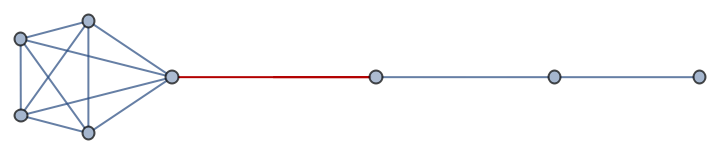

Highlight the vertices and edges:

In[6]:=
ResourceFunction["LollipopGraph"][5, 3, GraphHighlight -> {1, 2, 3, 1 \[UndirectedEdge] 3, 2 \[UndirectedEdge] 3}, ImageSize -> Medium]
Out[6]=

PlotTheme (2) 

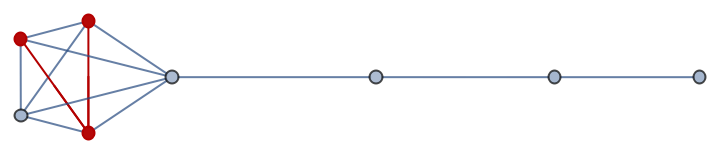Use a common base theme:

In[7]:=
ResourceFunction["LollipopGraph"][5, 3, PlotTheme -> "Business"]
Out[7]=

Use a monochrome theme:

In[8]:=
ResourceFunction["LollipopGraph"][5, 3, PlotTheme -> "Monochrome"]
Out[8]=

VertexSize (3) 

By default, the size of vertices is computed automatically:

In[9]:=
ResourceFunction["LollipopGraph"][5, 3, VertexSize -> Automatic]
Out[9]=

Specify the size of all vertices using symbolic vertex size:

In[10]:=
Table[ResourceFunction["LollipopGraph"][5, 3, VertexSize -> s, PlotLabel -> s, ImageSize -> Small], {s, {Tiny, Small, Medium, Large}}]
Out[10]=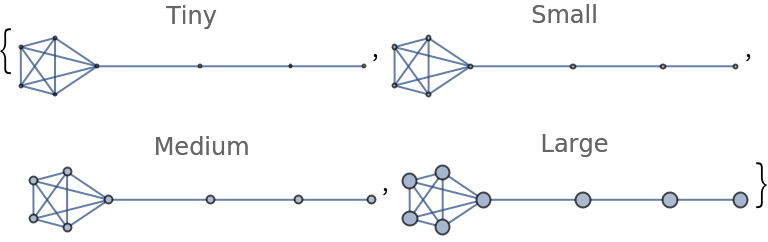

Specify the size for individual vertices:

In[11]:=
ResourceFunction["LollipopGraph"][5, 3, VertexSize -> {1 -> 0.2, 2 -> 0.3}, ImageSize -> Medium]
Out[11]=

VertexStyle (2) 

Style all vertices:

In[12]:=
Table[ResourceFunction["LollipopGraph"][5, 3, VertexStyle -> style, VertexSize -> 0.3, PlotLabel -> ToString[style], ImageSize -> Small], {style, {Yellow, EdgeForm[Dashed]}}]
Out[12]=

Style individual vertices:

In[13]:=
ResourceFunction["LollipopGraph"][5, 3, VertexStyle -> {1 -> Blue, 2 -> Red}, VertexSize -> 0.2, ImageSize -> Medium]
Out[13]=

Properties and Relations (2) 

Number of vertices of LollipopGraph[{n,m}]is n+m:

In[14]:=
n + m /. {n -> 3, m -> 5}
Out[14]=
In[15]:=
VertexCount@ResourceFunction["LollipopGraph"][3, 5]
Out[15]=

Number of edges of LollipopoGraph[{n,m}]is (n(n-1))/2+m:

In[16]:=
(n - 1) n/2 + m /. {n -> 3, m -> 5}
Out[16]=
In[17]:=
EdgeCount@ResourceFunction["LollipopGraph"][3, 5]
Out[17]=

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 22 November 2024

Related Resources

License Information