Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 LogSimplify

Source Notebook

Attempt to simplify a numeric expression containing logarithms using integer relations

Contributed by: Eric Weisstein

ResourceFunction["LogSimplify"][expr]

attempts to simplify a numeric expression expr containing multiple Log terms, using integer relations among logarithms.

Details

ResourceFunction["LogSimplify"] expands logarithms with integer and rational arguments then applies FindIntegerNullVector to identify any set of logarithmic terms that is not algebraically independent. If an algebraical relation is identified, the most complicated term is re-expressed using the relation. The process is repeated until a fixed point is reached, i.e., until no more algebraic relations are discovered among logarithmic terms.
Since ResourceFunction["LogSimplify"] uses FindIntegerNullVector, its results are not analytically verified. However, they can be numerically checked to as high precision as desired.
ResourceFunction["LogSimplify"] is in general much faster than built-in functions like FullSimplify. It can also perform simplifications in many cases where built-in simplifying transformations are not available.

Examples

Basic Examples (3) 

Simplify an expression related to Stephen Wolfram's SALT cellular automaton:

In[1]:=
rbar = 1/ 1296 (19 (-8 + 3 Sqrt[3]) Log[3] + 8 Log[7 - 4 Sqrt[3]] + 360 Sqrt[3] Log[4 - 2 Sqrt[3]] + 12 Log[2 - Sqrt[3]] - 780 Sqrt[3] Log[-1 + Sqrt[3]] + 308 Log[2 + Sqrt[3]] + 304 Log[-3 + 2 Sqrt[3]] + 6 Sqrt[3] (8 + 5 Log[-6 + 4 Sqrt[3]])); ResourceFunction["LogSimplify"][rbar]
Out[1]=

Verify the identity numerically:

In[2]:=
N[rbar - %, 1000] // Quiet
Out[2]=

In this case, FullSimplify is not able to simplify the expression and so returns the input expression unchanged:

In[3]:=
FullSimplify[rbar] == rbar
Out[3]=

Applications (2) 

Simplify the expression obtained using the divergence theorem to find the mean square cylindrical radius of the tritetrahedron:

In[4]:=
rxy = 139/612 - Log[1 + Sqrt[2]]/(12 Sqrt[2]) + (24875 Log[2])/(3773184 Sqrt[ 34]) - (10195135 Log[3])/(7546368 Sqrt[34]) - (422649125 Log[ 5])/(384864768 Sqrt[34]) - (3125 Log[17])/(2829888 Sqrt[ 34]) + (6948125 Log[49 - 8 Sqrt[34]])/(22639104 Sqrt[ 34]) + (6125 Log[34 - 3 Sqrt[34]])/(314432 Sqrt[ 34]) - (3968125 Log[8 - Sqrt[34]])/(22639104 Sqrt[ 34]) + (106805 Log[-5 + Sqrt[34]])/(471648 Sqrt[ 34]) + (2172125 Log[-3 + Sqrt[34]])/(192432384 Sqrt[ 34]) + (5125 Log[2 + Sqrt[34]])/(36992 Sqrt[ 34]) + (64658875 Log[3 + Sqrt[34]])/(384864768 Sqrt[ 34]) + (111215005 Log[5 + Sqrt[34]])/(384864768 Sqrt[ 34]) + (483125 Log[8 + Sqrt[34]])/(22639104 Sqrt[ 34]) - (2875 Log[34 + 3 Sqrt[34]])/(166464 Sqrt[ 34]) + (183308125 Log[49 + 8 Sqrt[34]])/(384864768 Sqrt[ 34]) + (375 Log[34119931 + 5851502 Sqrt[34]])/(9248 Sqrt[ 34]) - (5125 Log[41847233 + 7176736 Sqrt[34]])/(332928 Sqrt[34]); ResourceFunction["LogSimplify"][rxy]
Out[5]=

Verify this identity numerically:

In[6]:=
N[rxy - %, 1000] // Quiet
Out[6]=

Consider the definite integral of a rational function:

In[7]:=
int = \!\( \*SubsuperscriptBox[\(\[Integral]\), \(0\), \(1\)]\(\((\((1 - 5 \*SuperscriptBox[\(x\), \(3\)] + \*SuperscriptBox[\(x\), \(5\)])\)/\((\(-8\) - 40\ x - 36\ \*SuperscriptBox[\(x\), \(2\)] + 13\ \*SuperscriptBox[\(x\), \(3\)] + 25\ \*SuperscriptBox[\(x\), \(4\)] + 9\ \*SuperscriptBox[\(x\), \(5\)] + \*SuperscriptBox[\(x\), \(6\)])\))\) \[DifferentialD]x\)\)
Out[7]=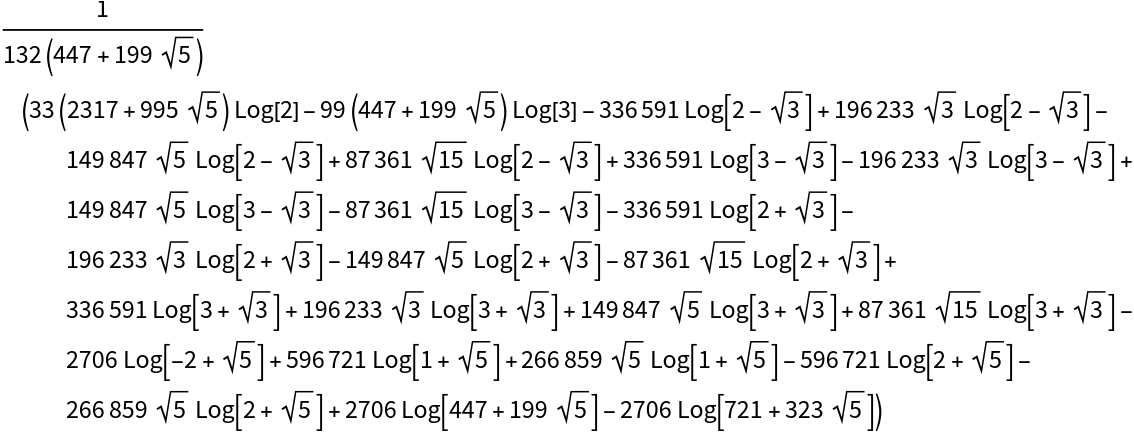

Simplify this expression:

In[8]:=
ResourceFunction["LogSimplify"][int] // FullSimplify
Out[8]=

Verify the identity numerically:

In[9]:=
N[int - %, 1000] // Quiet
Out[9]=

Properties and Relations (4) 

The function returns unevaluated when given a non-numeric argument:

In[10]:=
ResourceFunction["LogSimplify"][a + b Sqrt[2]]
Out[10]=

Arguments are evaluated according to the normal Wolfram Language evaluation rules:

In[11]:=
ResourceFunction["LogSimplify"][Log[E^2]]
Out[11]=
In[12]:=
ResourceFunction["LogSimplify"][2^10]
Out[12]=

If the evaluated argument contains fewer than two Log terms, the argument is returned unchanged:

In[13]:=
ResourceFunction["LogSimplify"][1234]
Out[13]=
In[14]:=
ResourceFunction["LogSimplify"][1 + Log[7]]
Out[14]=

If no relation is found among Log terms, the argument is returned unchanged:

In[15]:=
ResourceFunction["LogSimplify"][expr = \!\(TraditionalForm\` \*FractionBox[\(1\), \(48\ \*SqrtBox[\(3\)]\)] \((12\ \*SqrtBox[\(3\)] - 4\ \*SqrtBox[\(7\)] - 3\ Log[3\ \((7 - 4\ \*SqrtBox[\(3\)])\)] + 6\ Log[\(-2\) + \*SqrtBox[\(7\)]])\)\)]
Out[15]=

Publisher

Eric Weisstein

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.1 – 29 December 2025
  • 1.0.0 – 18 August 2023

Source Metadata

  • Citation:
    Using an idea of Michael Trott.

Related Resources

Author Notes

Based on an idea by Michael Trott.

License Information