Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the Liouville number or its generalization
ResourceFunction["LiouvilleNumber"][] computes the Liouville number to machine precision. | |
ResourceFunction["LiouvilleNumber"][p] computes the Liouville number to precision p. | |
ResourceFunction["LiouvilleNumber"][r,p] computes the Liouville number corresponding to the rational number r to precision p. |
Compute the Liouville number:
| In[1]:= |
| Out[1]= |
Compute the Liouville number to 403 digits:
| In[2]:= |
| Out[2]= |  |
Compute the Liouville number corresponding to 14/33 to 1096 digits:
| In[3]:= |
| Out[3]= |  |
Large integers sporadically appear in the continued fraction expansion of the Liouville number:
| In[4]:= |
| Out[4]= |
The Liouville number is very nearly equal to the root of a certain sixth-degree polynomial:
| In[5]:= |
| Out[5]= |
Plot values of the first few Liouville numbers corresponding to 1/b:
| In[6]:= |
| Out[6]= | 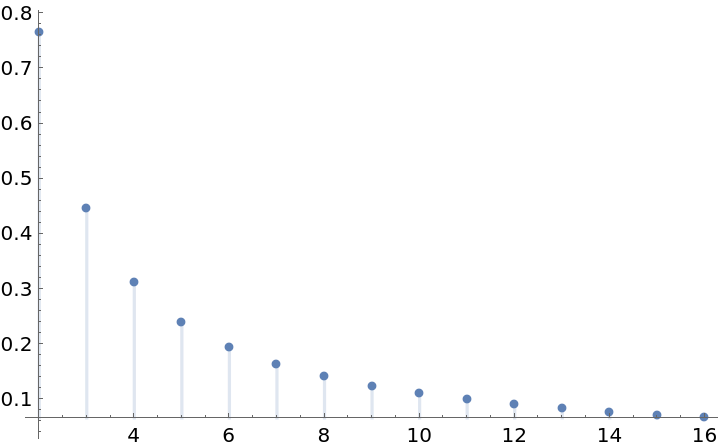 |
This work is licensed under a Creative Commons Attribution 4.0 International License