Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 LinearSolveMod

Source Notebook

Solve a linear system with multiple moduli

Contributed by: Daniel Lichtblau

ResourceFunction["LinearSolveMod"][mat,rhs,moduli]

solves the linear system mat.x=rhs for the unknown vector x, with each equation matj . x-rhsj taken modulo modulij.

ResourceFunction["LinearSolveMod"][mat,rhs,moduli,True]

solves the linear system and returns a list containing the solution vector and a set of vectors that span the null space.

Details

ResourceFunction["LinearSolveMod"] takes an optional argument with default False. When set to True it returns a generating set of the null space of mat modulo the given moduli. The full solution set is comprised of the given solution plus all integer linear combinations of the null vectors (which of course includes the zero combination of those nulls).

Examples

Basic Examples (2) 

Solve the system (a+b=0mod2,b+c=0mod2,a+b+c=2mod3):

In[1]:=
modsol = ResourceFunction[ "LinearSolveMod"][{{1, 1, 0}, {0, 1, 1}, {1, 1, 1}}, {0, 0, 2}, {2, 2, 3}]
Out[1]=

Check the result:

In[2]:=
Thread[Mod[{{1, 1, 0}, {0, 1, 1}, {1, 1, 1}} . modsol - {0, 0, 2}, {2, 2, 3}]]
Out[2]=

Solve the linear system: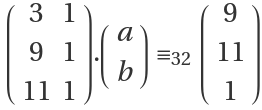

In[3]:=
ResourceFunction[ "LinearSolveMod"][{{3, 1}, {9, 1}, {11, 1}}, {9, 11, 1}, 32]
Out[3]=

Scope (2) 

LinearSolveMod can take Gaussian integers for input:

In[4]:=
modsol = ResourceFunction[ "LinearSolveMod"][{{1, 1 + I, 0}, {0, 1, 1 - 2 I}, {1, 1, 1}}, {0, 0, 2}, {2, 2, 3}]
Out[4]=

Obtain a solution and a spanning set of null vectors for a modular system:

In[5]:=
modsol = ResourceFunction[ "LinearSolveMod"][{{2, 1, 4}, {3, 7, 5}, {2, 9, 4}}, {2, 0, 6}, {11, 19, 13}, True]
Out[5]=

Properties and Relations (3) 

Solve a simple system of the form x=2mod5,x=1mod7,x=4mod11:

In[6]:=
ResourceFunction[ "LinearSolveMod"][{{1}, {1}, {1}}, {2, 1, 4}, {5, 7, 11}]
Out[6]=

This is equivalent to using ChineseRemainder on the values and moduli lists:

In[7]:=
ChineseRemainder[{2, 1, 4}, {5, 7, 11}]
Out[7]=

Solve a certain system modulo 29:

In[8]:=
ResourceFunction[ "LinearSolveMod"][{{12, 3}, {5, 7}, {2, 16}}, {21, 4, 26}, 29]
Out[8]=

The modulus is a prime so LinearSolve can also solve it:

In[9]:=
LinearSolve[{{12, 3}, {5, 7}, {2, 16}}, {21, 4, 26}, Modulus -> 29]
Out[9]=

The resource function SmallIntegerSolve can find the solution and also the respective multiples of the modulus that provide it:

In[10]:=
sol = ResourceFunction[ "SmallIntegerLinearSolve"][{{12, 3, 29, 0, 0}, {5, 7, 0, 29, 0}, {2, 16, 0, 0, 29}}, {21, 4, 26}]
Out[10]=

Check this:

In[11]:=
{{12, 3}, {5, 7}, {2, 16}} . sol[[1 ;; 2]] + 29*sol[[3 ;;]] == {21, 4, 26}
Out[11]=

Solve a system modulo 32:

In[12]:=
ResourceFunction[ "LinearSolveMod"][{{3, 1}, {9, 1}, {11, 1}}, {9, 11, 1}, 32]
Out[12]=

We learn (noisily) that it cannot be solved using LinearSolve:

In[13]:=
LinearSolve[{{3, 1}, {9, 1}, {11, 1}}, {9, 11, 1}, Modulus -> 32]
Out[13]=

Since there is a common modulus, this can be handled using Solve or SolveValues:

In[14]:=
SolveValues[{3 x + y == 9, 9 x + y == 11, 11 x + y == 1}, {x, y}, Modulus -> 32]
Out[14]=

Using LinearSolveMod, we can recover the second solution by obtaining the null vectors and adding a certain integer combination thereof to the solution:

In[15]:=
{sol, nulls} = ResourceFunction[ "LinearSolveMod"][{{3, 1}, {9, 1}, {11, 1}}, {9, 11, 1}, 32, True]
Out[15]=

Use the nontrivial null vector (the first one) to obtain the second solution given by SolveValues:

In[16]:=
sol + nulls[[1]]
Out[16]=

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.1 – 17 June 2024
  • 1.0.0 – 17 June 2024

Source Metadata

Related Resources

License Information