Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Determine the consistency equations required for a system of linear equations to have a solution
ResourceFunction["LinearConstraints"][mat,vec] determines the constraint equations that a vector vec must satisfy for the matrix equation mat.x==vec to have a solution. | |
Find the constraint equations that the vector {a,b,c} must satisfy to be in the column space of the matrix:
| In[1]:= |
| Out[1]= |
When the second argument is a symbol, the second argument is replaced by a subscripted vector in that symbol:
| In[2]:= |
| Out[2]= |
When Subscript→False, the second argument is replaced by the array vector {b[1],b[2],b[3]}:
| In[3]:= |
| Out[3]= |
Setting the option PrintDisplay→True prints the matrix form of the reduced matrix that produced the constraint equations:
| In[4]:= |
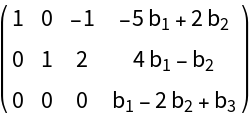
| Out[4]= |
The print statement generates a matrix displayed in MatrixForm. To convert it to a matrix, paste a copy of the matrix into a new cell and select Cell → ConvertTo → StandardForm (Shift + Ctrl + N):
| In[5]:= |
| Out[5]= |
When there are no constraint equations (i.e. when the system ![]() is always consistent), the empty list is returned:
is always consistent), the empty list is returned:
| In[6]:= |
| Out[6]= |
The column space of a matrix is the null space of the coefficient matrix of its constraint equations. Begin with a matrix with rank 3:
| In[7]:= |
| Out[8]= |
The constraint equations are:
| In[9]:= |
| Out[9]= |
The coefficient matrix of the constraint equations is:
| In[10]:= | ![(matB = ResourceFunction[
"CoefficientMatrix"][{Subscript[b, 1] + 3 Subscript[b, 2] + 5 Subscript[b, 3] - 4 Subscript[b, 4] == 0, Subscript[b, 1] + 14 Subscript[b, 3] + 2 Subscript[b, 4] - 3 Subscript[b, 5] == 0}, {Subscript[b, 1], Subscript[b, 2], Subscript[b, 3], Subscript[b, 4], Subscript[b, 5]}]) // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/034/034a60ec-dd44-4e43-b3ac-8a397976b12e/1dfadeecd161f717.png) |
| Out[10]= |
The null space of this matrix is:
| In[11]:= |
| Out[11]= |
These vectors are independent. To see that they are in the column space of the matrix A, simply verify that they satisfy the constraint equations:
| In[12]:= |
| Out[12]= |
The left null space of a matrix is the row space of the coefficient matrix of its constraint equations. Begin with a matrix with rank 3:
| In[13]:= |
| Out[14]= |
The constraint equations are:
| In[15]:= |
| Out[15]= |
The coefficient matrix of its constraint equations is:
| In[16]:= | ![(matB = ResourceFunction["CoefficientMatrix"][
ResourceFunction["LinearConstraints"][matA, b], {Subscript[b, 1], Subscript[b, 2], Subscript[b, 3], Subscript[b, 4], Subscript[b, 5]}]) // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/034/034a60ec-dd44-4e43-b3ac-8a397976b12e/14587b55b2ae2a6b.png) |
| Out[17]= |
The rows of this matrix span the left null space of A, since they are independent and satisfy BA=0:
| In[18]:= |
| Out[18]= |
This work is licensed under a Creative Commons Attribution 4.0 International License