Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 LineIntersection

Source Notebook

Find the intersection of two lines

Contributed by: Ed Pegg Jr and Jan Mangaldan

ResourceFunction["LineIntersection"][{a,b},{c,d}]

returns the intersection of the infinite lines through points a to b and points c to d.

ResourceFunction["LineIntersection"][Line[{a,b}],Line[{c,d}]]

returns the intersection of the infinite lines through points a to b and points c to d.

ResourceFunction["LineIntersection"][{{a,b},{c,d}}]

returns the intersection of the infinite lines through points a to b and points c to d.

Details

ResourceFunction["LineIntersection"] also supports 3D intersections.

Examples

Basic Examples (4) 

Fine a line intersection:

In[1]:=
line1 = {{0, 0}, {1, 1}}; line2 = {{0, 1}, {1, 0}}; p = ResourceFunction[ "LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]
Out[3]=

Show it:

In[4]:=
Graphics[{Line /@ {line1, line2}, Red, Point[p]}, ImageSize -> Tiny]
Out[4]=

Line may be used:

In[5]:=
ResourceFunction[ "LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Line[line1], Line[line2]]
Out[5]=

A list of two lines may be used:

In[6]:=
ResourceFunction[ "LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{line1, line2}]
Out[6]=

Scope (4) 

Find the intersection of two infinite lines:

In[7]:=
ResourceFunction[ "LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][InfiniteLine[{0, 0}, {1, 1}], InfiniteLine[{{0, 1}, {1, 0}}]]
Out[7]=

Two lines in 3D:

In[8]:=
line1 = Line[{{0, 0, 0}, {0, 2, 2}}]; line2 = Line[{{-1, 1, 1}, {1, 1, 1}}];

Find their intersection:

In[9]:=
ip = ResourceFunction[ "LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]
Out[9]=

Show the lines and the intersection point:

In[10]:=
Graphics3D[{{Directive[AbsoluteThickness[2], Blue], line1, line2}, {Directive[Red, AbsolutePointSize[8]], Point[ip]}}, ImageSize -> Small]
Out[10]=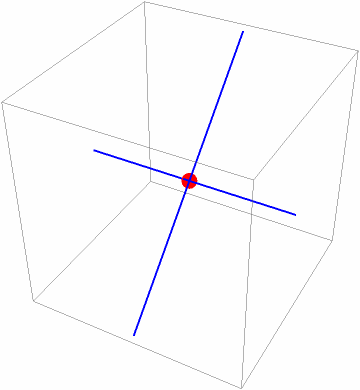

Ten thousand line pairs:

In[11]:=
somelines = RandomReal[{-5, 5}, {10000, 2, 2, 2}];

Find the intersections and get timing:

In[12]:=
AbsoluteTiming[ int0 = ResourceFunction[ "LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"] /@ somelines;]
Out[12]=

In the documentation for InfiniteLine, the following method is used:

In[13]:=
case1LineIntersection[{{a_, b_}, {c_, d_}}] := Module[{line1, line2}, line1 = InfiniteLine[{a, b}]; line2 = InfiniteLine[{c, d}]; {x, y} /. Solve[{x, y} \[Element] line1 \[And] {x, y} \[Element] line2, {x, y}][[1]]]

That method is slower:

In[14]:=
AbsoluteTiming[int1 = case1LineIntersection /@ somelines;]
Out[14]=

RegionIntersection may also be used:

In[15]:=
case2LineIntersection[{{a_, b_}, {c_, d_}}] := RegionIntersection[InfiniteLine[{a, b}], InfiniteLine[{c, d}]][[1]];

That method is also slower:

In[16]:=
AbsoluteTiming[int2 = case2LineIntersection /@ somelines;]
Out[16]=

All three methods give the same results:

In[17]:=
{Union[Chop[(int0 - int1)/1000000]], Union[Chop[(int0 - int2)/1000000]]}
Out[17]=

Inexact values may be used:

In[18]:=
line1 = {{x, 2}, {5, 3}}; line2 = {{0, 1}, {1, a}}; ResourceFunction[ "LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]
Out[20]=

Possible Issues (3) 

The lines are considered to be infinite lines, so the intersection point may not be on the defining segments:

In[21]:=
line1 = {{3, 4}, {5, 3}}; line2 = {{0, 1}, {1, 0}}; p = ResourceFunction[ "LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]
Out[23]=

Show it:

In[24]:=
Graphics[{Line /@ {line1, line2}, Red, Point[p]}, ImageSize -> Tiny]
Out[24]=

Degenerate lines will not return an intersection point:

In[25]:=
line1 = {{0, 0}, {0, 0}}; line2 = {{0, 1}, {1, 0}}; p = ResourceFunction[ "LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]
Out[27]=

Parallel lines will not return an intersection point:

In[28]:=
line1 = {{-1, 0}, {0, -1}}; line2 = {{0, 1}, {1, 0}}; p = ResourceFunction[ "LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]
Out[30]=

Requirements

Wolfram Language 12.3 (May 2021) or above

Version History

  • 1.0.1 – 29 November 2023
  • 1.0.0 – 14 June 2022

Related Resources

License Information