Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Fit a line to data points in n-dimensional space
ResourceFunction["LineFit"][pts] returns a Line that fits best through the points pts. | |
ResourceFunction["LineFit"][pts,"Association"] returns an Association containing properties of the best fit line. |
Fit a line in 2D:
| In[1]:= |
![pts = CompressedData["
1:eJwVl3cgFY7XxmUL2VtcXOu6xnWneY+dIpJUkqREafgpviF7FC0atGyiSSpZ
dY9VGqQks5KyKiI74vX+df4+5zznOZ9HzfeImx83FxdX6iourv+vB7a+sohJ
m+aM8/3OzPcY4ni+m+yLCZMGO/5ksb10WdT9FHP+Cb8hvvtTzT43ygTz4ImA
72/qOEnrhyI4YVxo3t8RVi4tAcbvi6IsvNRQMtp25+9LJCz/j/RC3YUJN+QS
Eu106fhOEj0eylqDVktUWsx/hngv16shimoKtt31aooMZXCXCPi2VEBAj6xp
ieB5fQSuxnt5tUzoyP5FrnPWhUm3+C/Z2sZ4LCRdXewkEUM8Qg79mqDA2qEz
nWrGEnjgRMirqBwCDDgdIboMk5BLkVB8Ip4B56M3Tfqn0TFoYj7i2V2AQvfu
Cv5fRHRIkhOeTzaCO7Eth5PshTBotOIulkhDT6sc8wqvLgZqC23L2kUDZSG3
K+rFDKweknZsj7SGnn/Tz8qfC8PYrM2o7/k1aPaK5HfMfy3eCPGpe3tWB1r/
t26r2QV1kLFbxho7I3yQesihxZ6ADMPHDv/F6gK5sWRmtNsYP8rxbieuB9jS
6Zl/4Kwe/CmKyftlycKrWsfyroIEHmWz1utvIMDp2wXy15y48O3E2VdyKtKw
+87n6SOGfFCb4CVfv3OIczlu/dexBhZ+493B5Z5oB+WLuzVEhci4oNxzzi+e
CceC6bvHaDzw5zN5eTZcAYvCLCK0h0zQUS0297imLTw3JU9HLBIh3jRcq0+E
jhKmGm8GF4jgtVUgZDLLCFcNbsdAPk0ksfnqj2tSwXKhTiPnOhFP6BdciCgx
Ar82hYTgSl0MT438cj6NBqvdYkQjRX6yS7+Y1+XofuTE1crP2943BJt91s9I
TSx0KN9V41RthLPr64RKcs0hL64otXUbN574skcxuUUBTEWPmn+8ugquTPld
Me5ZjSfPLTgkXtUGM4JAVxKJht+u2Zd576Dgce/FgmwKwGShkEShsAzsoLfd
bPQnYMGu6yMxXVpQFbHxl8oBKjZbUP5sVxGH9F7/Td22yigfmpGV0EVFGiuj
bb+5NYjXJRyWSBWFzg5Rk01pyqjiteCi93SRs/QwmPR4NTcQ6OwXBz1o+GhU
sbyBDPBlz49PA39lMOt3+f3FSUUYU4ka9CAKA5Exd1JTVRD/tp1Vkx4nws6M
ysn7lUbYvM09TtdXA/G02dHmcwYgGNp4al01A2XV/Sx3ZNrAuF/tn3BlQRiv
+H5ji6MUBvD+Z3t3WBy/Nw63F/4WAH1erudXf3Oh8L6P8h84MtCPL7J2P9bF
bdEV95CXBpL0euGMCxOcuWabahAVALF3OdnqgTp4Ze6BFUvLGBT6ybsvF4mC
suLPG3vLZbBBpCVUWJ6OuwJ1XYu5Ad6VKa0dztaD88bunRQGA6Nutqvt8qBg
ocV200hfc2CGwsBCujQIp0aMW3cp41XbT8eOrTfEHUJWQs6+LOiL3RP9Rl4R
YhrmHuXMEXENZftVH3VtMCC9HODkGyHV+9CPvRsMsPRp4hbtShNollAN8DCl
4o26fyeK7Kxh4ejL6t2nydBld3SifIGJiQ+maYQsIdxePEo+P6EEt49L3bGP
VcOcgORbpHN6MFaXVdFaoATnyh+5b+zRwcisEb5d+VRsFUyReGsB0JL37G1w
Bxk1Lxs83GhCB9tPlIMOkopo7WR6Y3uFFrxP6rgr5KYMdWNPTP5mquMk4Vyg
0xlFUMlcYk+raOI1JcvyTgkhUJGieJl4CGGwIsOo3VgTRP1pW0vHjPBxiEp/
2Kg+yk30nE4vY8COw8PP/roTMO6bXrRjjz6I751tv6z1lR35VrAqrX+WE1bC
vm+rawAvA4Vp9RtX9H9VXq5DjQTZJtn6eSNUbAq/zi9krY7Xb8Y2/RajQl6u
VH1xjRbusTjWMMDLgKDxu0v1/dqoKN8wYLJAhbm5cx9TDJUw+5V5jOw8CTym
J5k+lw3AUckZ/euZuMdfUEbkCgEWD+2jaj8h4YEn3jsjDpJR5tbwukuqTHjJ
H1ZzYbchHmrzYhY8ZcKAaeJluW4NSH/33fzigCGebrpPL/QXBiPl6p+pnyTR
lSvhbpmFLPC20G5WyauhU92fjOyvTKR3+ug36NhC2H7CwIcgEvi2idz8FcnA
seyy/c2+wuhdh5rfvsuDhrCd/9uPVCQdvkKh6FpB+91rL1+SDbGsItW+V98U
ZEaVO531idB5OMGYnE/GtC5p1ZphA5SK3Jfl9cYU+qSTLITf0XHqU+qeeIoV
SDQlPBxa2W9OWvDii9OmcGcXQesInwaetQ8ROvtYD3qvvMS9rfzI8hfkrdYR
A/vD4t5Nlaq47uFHj1gzXXDqaN18NpiBf5+V7hUcswXVxVmF93wiGKNqdcRW
RgLCCh53KGRLg6Llnvg9jkSMWNi7f0GdBA+KZq7wdNHRzCn1seUUC61kb38I
bLSFKwrthnXyNLycfxy6+K2gzdF35HiQDgyC57vOszRsLU5xw5X7LsotLmmz
VkSLmpA54+hpjqJCspTvWgm4/35+QeSeFo6+cLMVCl3Zf6ZWbMLIV3bp2gr/
17R3HPlGTda2UQFwCw2OjL0gj9I5+vpbHbVQSLqtb8cnI9jC2SYs3qYOC6ve
ufLpUfBXf15thwUDeRzdFGTLbOBxqndMXIgRSv6kv13QNINR2aSW7Zu50bqw
6q+0nSA0+V8aOaXPwmD9z6NH/ljDYV7T5IyPBuBKmg+lnGGi5YnO4eVnSljf
vIrfo04PYtpCBDeXK+HB+xuapzp1oNRhVGPxPAkd5i5vOcumQs5TVVk5sVUY
PZM1MC8iBQf/M1FWWEuAh509Iz+3k7Gn0Pt+6h4iZP4uHdIqM0LZ0ef/+77G
EIyHLyrG6zPxlHOE6qdjfBAwE6oWJCCKz2UO+YZ2E7GmwuX6tgoKBMZ6ML3D
DSClpefijRoaPmdJEni20LFmu2r9O1uAwWepLhpHlKCu/1f58z3q+MFXRs7n
jSbY2HIlemZSUHGDbm5TDwW+jO2TNg81wWPjw6rOKhTsuO5yfJW0CdgFLIhT
h6jIczM4jlcM4J+iLKf47AQnxXlBaHnDP3Zks9k1q990rEClgqCV/1OV70qg
BEhjas6mE9usFWC8WiNts4g2KPZNqM8S6NhZJjuF4mKQ2WJQxaJI40V73h2J
Ihr4da/CxEI6BW789tQJ3KWDk+FLJtq0Fb9aW3BJ7Rcd6z8HbmOVW8OzAuev
R3q/sw2F/isx5x7hnNJ5L1N1n4k3c7ZWCsnZAHm30+PSJ9LAYtIuix9TQs92
no5XOquwl5TmWKekAimz+Smqtavh0Jm6Ea5EcRQY1gz9V68LA+HUuKpHK30c
lxydq9OCMt6jw7tcjfGRY226SzIVS13rKYLnrIBvUSg7W9wA9l+fHXa4zEKb
63Mdl3sn2OdmNEMjdcc51hyeWU+XKY5jWXtf7TpROPXlfiCMaeKGjrOoKWEI
5nuUz7VGK+FOmT3cRbv1oGS3sF97vwZavRlV3H6cAtv+jpSdktXCfAmiddUQ
BS7V/rXU0frJwSn/dHHpJk5YT8Nxp0uyINUSvIXUrIF1JDV9+1MiIFNxt3W9
vArec2h59q5JFsLFpFO/nFDFPw3EykoCDZOsJrvvelmCc5wlw0CGhXcbVZc9
c2xAobR2QiNfAjWGplItG9UAKhncTwYNUUjr6ITAgCnsiUjvnd/FxH32cj0O
AraQXON0RVl7gXPj0Sc+wyBBiBrVfjUTQMKo176nptgsIPHXBJR6GOHwg6mc
X9xmoORJy6nM58XScpJKibwCuG4rHLu7ol/xRIE7j9so8FyRFNznycL1GXnL
eQxrMDTyKsO+FR64q7/ou2wDH0KzDaPuk4EkdKemLYqJOZXG++8JceOjWwP0
wO38MJ8aHPeSTceoLPPs+EwrmJ2a+kxc4b+3KbMHKCO2YCv8JJGmRIa4aq3h
e3F0fKZB3qW5j4hL3478KkYjYNVKZ9tZ6oOYGFdEmB4Ln4SfvpthIg6Rohcq
P8erYcMU+c+lIQ1UfO57cA1LD2iJDg4/tBXQuuLA9K8TGnBneZ9+V8rKfNN3
D/h/sYLWbQGvuq8pAudH+saXQVoY0CqhNuFJQ0WnvQQbfjYM1g6osmZpuMvG
SeGPvTX4BPyXY5UmCU4au5RGfinjMREDpUNVylgodVWkJ5kIh9bZPt+awUKS
QR9J/KgteB1/9PR8hAA0pZocZi3w47P84C1f/qlAkKGVdgCXHja6xL++pqeP
++vNvrFnzeDbg/GLNreM8GU+rdkrwwyefKfl17nqIe9QCnuKzgR7e10ugqwE
3soQ7FedIEDq2xGJwEIiHjwy3B60mgq1jsEMD2V+HHEe73dRUwS5YbXlvbpU
PBGQn6FGYsP6LJ/p+jQa3vJDLC+2Aq3nYZ0CQ8rAp7OlPzNbA4Pur/NpeK+I
p3064rPiNcE8fY2b79vX7LnIcHeWKz+umXz3uNhXEpMKD8ztEJYCRc2H4Txb
9EH2YGyX1wILW0daLz6+R4bgzIIwA38G1gUXb9uUR4Ciz5b648m6+ErWfIPj
AzU4bxPtqOhGxnUzmwz979KQOVP2oOcqgML0yJF7K9wuzWqa+S1oAeOuD8rh
jg5U0vT8Di9Rcd9u3jgzs0UOrcnvzIL9F86SwPj4uVW8yEpd2xiqwg0jjOSl
mzWqKOXc9r72piFYtSSs7gnWAKYjK670tjFGkqzbdVzVgWpTPhGcZYDrn+yl
3TmmgwH29slmZ4wh9FdQ1KdNEpj5WvSrdggBtuRapu91k0VzJ78qXg8NCOIe
XXijoAJCG9XPrxc1wKWGMRF1MSpqdS5atb23AFf3iM7JVmMcahLf5pRvBuEi
pg0umpLIolo1SKsoQqPWyIDfqBpO32+842hEh+9Zydz73NWAsfQtQz6IjOLX
owO4npJhkJqbU9DKwHt+dlWPZ3WhkVymZLfMxA8n+y+6RRnAQQVBEwdVFhrV
PVq1rpiOBQEPuuRjAFyKS8ut8sVh8pV/tRZbHWUax4PFVWUx+G3a9YrHK3Nc
7Xl7+b0pejWSPic62cELCYGA5geqwNgfLn7fnozIZ7lq37o5do/PX1q45xC7
GGoK+5LkcXFnWkGMhCY0JrYKHXWXxKvJb82VdksBq+Ns3au9RtDfHfvio5kJ
epCiE6cUZHFTXHmEqLAGpEgKO59W1sTssI0aoy0UqFDOCcw9S8RvCpzBL0QK
BHk8ftLewEQTF9SQc7aBvET+VdFgjI07jijZEwG+7ZEyeWWgib3uE8XFlsbw
bYfmGtdJA7xwUaX0TQYT/hwK4Ca/5gYDPCfNxyWOH9V5vNNOr+hT6YvdJ3cl
MHD5vf90oyTMEBbybA8Qkf+m+aXyFEmQrJhReROggdcUWCX/zsnCrJhXbrG+
NnYJNKzdbG2I57ZZrF9dyoAm3i+57Ztfc4gu2u1m8Qtsl6mpU/Mr/++nVn52
QxUZwiIYm+R7NHHkx76MiVVUWJ3hG9povgrOXV7X2pLNixXm5Vx1gg3slyTt
ZCvdCU6LUuafdjFFrA0x/qn+TAPubXkVVraSD9StFK6W1hlCfun9il2riZj8
dP5I2x0K+MxIZW4YYWF89Od20Uo7SBDY6+mtSkSboabTE9VGUJi0vqx0uw76
DLr93HeQBq53QAokNUEyf8OzhEP6eGv9OYPVp9VxyfUFsegaGZQ9qkQTYqWh
dswRYwXVsDD9XepFAQImMYR4DITIkHSXELq1jAeTptIM8rQE4KzW75f3/hHQ
/l/W8gtvMqiaxjD6TmrDpubWb91Txrh6A4FOX/ErY8p/1cshK3p33VHEP2eA
psuvrkXJmkDvMzGBpEtE3N9l51J+wQg+U3IiyWspoDczf6r5Ewvpvz7cu2/G
wGt793N09lkB1fE7z+lIIjRatKhtuKaHr8OHvBUipfDnuHOOzkkCTAtRlnx3
9HHIB7VLvm/mhyt3Ym0EA2XA/s+1I5LHFVby9deNj9az8E6Naa8ixRYsymob
LmyUwU+MQ84ir9fCTRlPj//4tGGzz/uL03009F59+qh4ly7ujHf+EDtMAU0/
G5ZcrxIMuM9cYgART16M5/JapuK2V1IbvkpZwT09ow/CRFU89IFVINilDztZ
l0rXNOqChYpR7GTACs9t9l10FWJi9txq3rPJ1mDMfcgdxSl4TNLhfneEOcSd
VFJYY8TEt3/H9KwbrcF2oV7h/LwcPF279bCXiSbSJgMuTvIJ4XBp7ZmnsTJg
666zm3fYFIsbWld1/ljh9UGidW7aGnT28xSW+K0E8cdcJhIfakOgnk9OPIOK
Gz1JJUvBmniif8lv4pQxVC/8+9Mhb4qV070vQ7vtQHB/9JXbR8ko0fVeaG8K
A/IPTgrF7yKjx0b9lFsnmNAcX65Ek19irxbe+d43SgbN3lscNl7JF72SASlT
7eJgczz1fK6GANz41FhzsJgfNS0Ux/f8XWI3i1Ycun1bELdWMrSCHXRAt+fo
s/50Gn6puH5WK5eGzgmHvx+pt4KEAw+83x82hCVJ7kpIZKK70eLvJDEybPb7
XtLOYOH5kCyXOfoMmyvD5GZR8B/2lYaaes5OVSyqehrZQNCGb/23v1YZKYDC
VRNmWxgBZQy1ooWjxfBJagJXSaQCqPFGxyVmKMCjF17icmpElLQ/8TVshowl
fIXLktUsYDiqu0hL0zC5k6f1Y5IlTNzy3TLbrA4/dxSX/CdKxRTFA/bt+Xpg
uJcvfm4VDUtOuoeOkYwwYHfNw5t6FtBh+/DG2LQx8hzdHy58CsDtsFuA/hoN
vJrxQXKjKhUK9z/9nveSiYn51dsX19tC7taQNo8pEzy+cKqv1dwO7PSFPL8v
z7L/l/LjgJWWCL5X5OZ9Ovb/fqbpIllLh62nlku/ehmif0y+YtBxU9j6b8ad
ZGOMLfs6j/E5mcGL+aKj21/pocQGrm7qNQZQt+UfusRPgB/vLa03zRvix6Oa
fcIhCxyfvWfIbdytbI21k118O9XhVtxPwcEbBljsXaDRvr2bnbyKy2nDLxEU
iRbreWenAHa9H8JUldTwekqfSKUzDd+5Ee9veWoFb+M9F72tDTDEtlutPYcJ
tYb19EOZ2jB66/kZZXMG1r9YT6/pMEbfQPtl+Wo26Oc51B9114GJ63e7dAap
+MHoSHLS6F92nd+vnQ7+PGgU7TJetPyCfW/TnRM8btLoI6J/vPf5DDtjWOTN
SN4yZzW1ceB1kSwYiHMNhCioY4tOp5iXuQFSPMUjiktYwCNvH6h9noAvHmqf
GDc1grpTLep6BTzgcLPm+lMxbjTnyt2qfpcAAXi1UfyFLubXJzzdRDSCdV4B
fOaZTLQdGmqNvaiN1dnt7i2JVLggkbmLKCGDoYFNe+r5teB/v4sva9SpQ6NM
hcYZfgpSFeeH8YkMBrn8nY9kqEGKbEF/zZgUDHoXhf/crIb7q/7nmOpOwgje
v5fUgxiQmrZ5R0rsHHvdix8tm68vcqJSCqn3crSxlP9csUwXHdQOt02qzhOQ
4N+60/KFLlibW2k6XCHixqKikBFPKmiujS9Jysplb7viPfp49DMbtTV2RvRP
cw5+SiT8ZvPB97dRC7xXqej7gb0jSs8Ges1MuSUDtZB/zenF2ItUWMO+WFe1
SRc3OacIZc2z4MBw6Za4f0ykrWku5Am0g7c3N51uKJSEXiYxceL3WkwfZIRm
ujGwum28u+qFNYjlqHYOFGhjt03j0bGjLKjPd34SFmAIemoH1awLGag5KHxK
w1EMr1T2v67+owyiCz/HBw2FoVll94ZKH3HM4aS6mN7Rx1B7AidJkwnr/4Zt
WmerDhV2lz90baCgr171xwUBOrZ+lnvrcMYKBDTYONKugHVBn46MryHC/FBT
h90NBhZFz9Z0kG2h26ydafdAB9qUfsuaH1nxi7GQmKGuabb4pEpPodI7ztek
oKVHCwYwGWgzGB5ggn2Zl8yfe8pizIyPz9URIkRFy2ZclhaHp/e8AumGCtjX
oGYrUSKO9MgYck2LBnR/DpQxfW0EBUq+fTwhTKzSmDrRlspE+tVRx1+fbKB9
S5Bg/h1DYOelq0fQTZCkOv1qc7IR5tkn2jPdzIB0LNVt12o5TO90S6iPJ8K7
bOncxAl1EH7ILf4jzBh5/81re12g4Mt1SXwnlMzAKd61xewJCQZXLXbXxlPx
5BnXK1RFVRx9O/aQUEaEbx2TM2nmarCZh2nMn2uEng+Hx4lyVFS+fbPpdjob
GnoTpprkGHi6qncQf1rD/wHgXZIn
"];
fit = ResourceFunction["LineFit"][pts]](https://www.wolframcloud.com/obj/resourcesystem/images/0d2/0d2a067c-c8a8-4862-a551-3e7b756a3b08/0e57ececfa343e64.png)
|
| Out[1]= |
|
Compare the points and the fit:
| In[2]:= |
|
| Out[2]= |
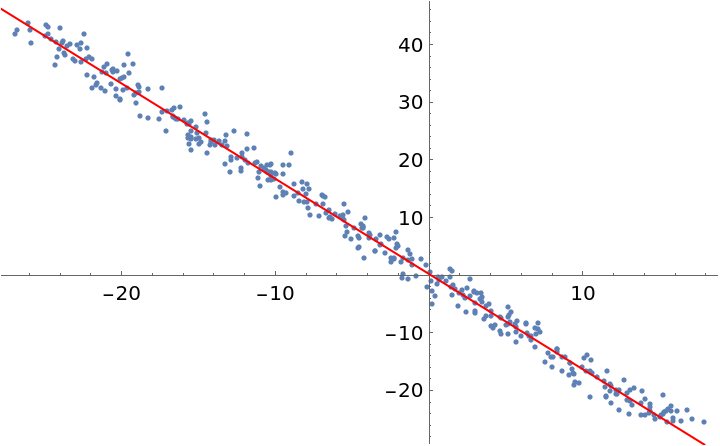
|
Do a fit with points in 3D:
| In[3]:= |
![pts = CompressedData["
1:eJwVl3c8FP4fx83MZO9x5xyHc+7Onc29jaT4UqiMVGREklGRKFJmaEoZZRSh
Uho03LslGYWsSqjQQoVKMn5+f33++fzxeXwe7/fr9XwS/Xe5BfLx8PAc4+Xh
4V86s1zO31beyoY9Ee+SeGOIeDlOpD3UTRtvPS2U6DphB7+0zfZfG6XhniR1
TzFxFi4HC4WaIRWkeN9UMHLhAYernAuiLZLwSvWyzjJnC3Czr0z5/omMLKdt
HwSu6GNnhtUBnccAfCW9TzaOGOJq4pOpcGsmGo2FDSWM2WHctn/D1yMY4BEs
NUepMQaGvJbIyAV1PHfa61i4oAjcsTzl1FcsBFVjXWmlfmy0MV/fKhJGBHHn
jwwpGy2I8QcBGKdDRlimdBJRAwvayx2HKrUwb3rFNkKWEYoI+9Fa1pFh6M+Y
jGOyOvh7r+71i9FDS+oXI83vInBrjxD9lacq2J3fp8xjZAsTaZ1z8lsYqP7U
ythgkoUUA0/qYp0+Dn2Tp41GqUD8tv3vijapgF9UIBYDExN4Xjk4XCUAZcGu
6DedDIW+nhfjDtJRX/RYZ1+3GmydTr21Zg0RLldxo0I3kiCUvJWQGiuLqe89
D7Mj5HB4XjH2p5ARfFh5L9F/BxGDXpCCREs0UW+tZJuyJxvqArLiym4TcfNE
NkfQQxvHGJFNUrt00XR/N4lF14CyzT0PD3tpgoeG7YnGJAvA/PqLxgNaeG0+
xXW6nYpeltnWGleYcLP21p3vy4lo7DUdqreMjCf/+zgXFWmH7769z3xaTwfL
qaFJBssETuZOy6elyQJr5f7afZLCaKzT+av9rQxWpV8x3phqD4mJ79nXD9Hw
xDHagQ4tFuZNqqRuz2fC5J+nA9G7NNC/2+PqU3cy3h6uyDopaA8tZ+oVr9cy
kNQTFj1yi41vH47e/YWm8NxIv8W7TwsfqlbEpwrpY9YbwQvRsRxor2ht/Jmn
jRmt/kNHqDSMS3Ys+jPMA4meX3RFoy9xHzd6Xdd4L4gSFHkNlUhLlGy0tD0w
QwYyN89VM98AHG2bCs995sP72/XYsVmvOMY3Unlrz/3kjJTmOnzdZAv3Kskh
UtcNkbjzlfZApBFubayMkAg2xemHecNJblogdi73/EitHkjVZg94HVCGd8Wn
D33rXeRquF+Xf78ojpXlV9sv8dviprHdoc0TNIhQeUM97WQEQpGT+ZXFy3HZ
IV87GfIPzqWDFT9cIwRgW4MVf56CPfLdPfQjpIkOgSfUVOd4jOHksc5t2uWm
2EMvfyegQQFxheY/RlM6IF/z86b4fnsIz9i9pt2ciQPdUtmS0WzUO0JpVTTm
h1CudcyvA484R9/MDr0THuI+bY5ePDVji6EFBp88hOkQ6jFd89KEBVuj9u1s
NbLFOv0rpr29NHBefa12rSoThH1y60J2KYGYp/GgxlVB3Dl7R+HCY2ncVHS7
R/q1MfTn1Hs+J5Hw08xkkHa7Dh55xRFhZltBgZix3ksdfTwoOSzt60dHBYKX
Z2WdFRJTCxy7e7Uh7XeMq3AGFSY/ZH1QmWOg18Ca6ZexBMhRfStVEUwEL56o
K2+OaMOEmj65DqTR6pdXPHuZPPpaPM4h7yFD1qot0o9GFLDsa8tUVb0kep9K
PdE/aosS/wWtWwijwnSeZrzlOAvUvP16bt82wY3Nwyt37SDCCuEZbfXduqAE
pvxpQjY49GuqdMqKCt70w3brTtJB/sGUfH2FGTLkqz+c3U2GXkXFlQEONJD2
DNGtqyeA4HX5EpaAMA4XefDG7JPBzLHdbnfdSfCPwdJPviuHDZmzBXrm8mj7
WrlTtNMCfbQcVx9eS4FVf7Tmz0fqg7JK8HmTZYB7yyyoU8pUePi20vJcKwOK
iArLZYKtcNhO7a4VTReOG8WtCowxhJ8afZxfl/WhOMEgc6e+ElYIX8hWatNA
c0dH3LGDjW3fovdazhDg5nHlaJlzOsDXKc9JKqbD5lvb3fy+KOPtZ6+597OV
sFGjpDzpqD72put8G16jBud6W7pS6lVhUSzhmIOPCZwtKGo61qmF0vSMvpU/
abhGYqjAf4MxKpQ9+1L0hABOibVEmSxdcC1cPaS3kR/vpl2iCJsJgBt1Rd+O
sz84whUH4sUotniFd9O2k+P6sL1rIOvYfSbIpNX+uShFwpZiEb4ePTlYZJuf
Zo7LwKvP7GmnH2zUduuLm0vThOQNJsVrjujA9ELkc5ckQJ7JWtoTDTqEBd0d
CSEbgePywJW+n/TQI6BUIUBBDihVzCGzT5LwL3atNu95W7g6PZoeY0vHuDDn
0jE9Nm6djLrW7GCDjwp3DJ/TosFmlemRR0eZMNX7LUOpwRzOOdn4Oq7Uxhvz
HA/5fCranRloLzIyhpUC9p8piZpov1vZLJVPGx/oDO05HcFGd9sMIUoxCWxy
PX/K52nDDpqdX9ttEvRZPjpqOCWDtR6Xk1PPyaGD78fn9Bg2HOj84BsfS8Lt
yxb7r6uRMfrnNnHLVjscsbl56oEeA9oasHxdqxE0DfssdwoRBsaKI+2m60c5
tgmvV992FEZhtTfaocFSeNg9uC57SBRyiruAVSIFtye7UjIS7eGy//NDK/Yz
0IppcfvaaxZWhWVeCzW2gsXVW9ap3dBFjcgh414HOoa3btTvOKUE8fd093/S
4EG6VfPjD/7LUfPG1/esq/pornVtnYG+ItxOeFXvzCLAH4Wun7bxonjj98oG
nn0zHLP7jxacjkxwSvs86U65Zqj2oNl1dlIH7KtFB8beGYCxN6/iXJkFCu3x
RoUWLVhGYFXxXKZBELOEWKXNAqtufaOdnurIOs0fMxagg9XKtR+TY81R5g3l
BkNUB76cp5gvLtJgY+j0Z+L6Lq71F4N7aSW1nIj0OOrHy+3cvJQmn5Z4c9gT
efDwnuVL+Z8d/kmvVhfPB8/o2e5aDnz+aesani1ym2NckSLHi00LQcJsHsAd
HtGyro6GoGk1NfLqylJfbYvourTdGq35Vp0eeKwHoBIZHBXHgGyqg7Rjlx1u
ueleJZtDh8taMxZd/7FBQFL9085Aa+QN8XW9hxS46T5gu96EBm09cdWcnxZY
WpPSM+ipDdNuNXBJjgEOjYMBoXlvOQH2+e+KH7zi+ApJbtyZOsG5i+Ojn35L
o7ZCckrqPz5w5H/EHHAWg7L9BmkWqWPcx8Wb63fEjnAqF1eoeC1/z7m0Zdcu
qzKA8A8RJ2yoVKzTUbe030rHbln7YsqMBe6t+Sv41ogKm2SNiygrl/Z8pSJP
sA8TxKtnjYsJRKyW+SbwJkwTOzTbJC4S6Bj/2OWXerUCvNxse7pYnQRl7z/z
7xfXB2tH1TbqTiKWJqUobLdXRNMvJ8u6iiQx7uxx21Ouo1yNshxCtYUIKGQa
Bf4qsof0sWOeH0foGJgpWbDCkY2jpYqpF6IscFkfpNy1W8pp/zv+9UNUMPzd
m985YgJr6ZAcYEtCA5vluTVBOugbrLAvodEYrQ0fbt9poAeeg8MMKQNdmA8J
a44VI+Dz9veXLGz44c+/rFqrrRKg4WS9zrXXFvzfvTiyH+lovUEw/+gSX/Xw
PEF/eXt0T9m3bUMRHdRmw/Y9rmTB3SLVpFYnHbhKL7owzS+J0QFdP32s1HFt
6xTtx6gRnD4c9OjLb020MK6puSlNRD9JKfO1sSuhLrE0RC+TiWcd4x+st2Tj
79cHzFUUjIHy4dmN6QtaGOLYd0KLQ8aUJLuhjk1M8LaJHJ+ZJ6HTaNHTz6+1
sFb5zoZcMEWTd61nOohkECP8FxslRoGVzuucFealcWrj48pX2SKQn7mvNl1I
HATvXs7R4LfGS/1T5xXOa8GpublRIwc6bN2yWJCwnA99NhYIPsr9zD3rP1fx
SVUSli/cuzR+hIYNcyXsMrYCzLgOjovEqAPT0MGfzqeL7z/JdVqcUIARlexM
M2V1CP7wH8+2Pbxosv+SgvqJAU5UYemd+kw++Jy04tz4ISp4epY/7C/RwIW/
Rcffxyij9BnJF/trFKGI00tr3MuPEy53ahKnBXC2bJ47yWXCBoNrG41SFNDF
YsXurmda2NjY8O5Npj3MD514ltjGREOpmq+8F1koWLZl3C3CCjdu++K3T10H
til6X96xgQYbAj5OvcvQgl+nX/7eniWFRcvCrNf3yiK75IZa/5cfnL/+wbPz
L79xJzSNIxu7lqE1ZeCVwbAN5naGHefjpcMRFef9XnUMsL5kHt65iYFdMRWG
JlvVgORb6HxogQC2DxfWXxFkwZn0rcP/6jXx8Po4jswIGQUe659ZS7WFkj7N
4wtsGr6NZLF5ppl4jS8ugCfNDF50/f1wJkEHBatCCh5ZUtGpIeuGA5GJfAQP
1fFIEjAvfza8Iq0N3e1xd0ZmLVGd735xRbg+3JpNk4uqMoBqTVYhiTjF9Vzx
p7OsrosTVPTf+OWMV5xevzspu9cYw5NSYVaqhSbOfreIv+KlhTlh5dYBfDZw
ic8lfWcZFZvTclab/2CgLWdtoN5xXXQW7fuQqSgBl7RSktZypOFs3DV2WakW
1iVd9AoUloOb2cKeK16rQvLPT2r1aXRolDISpc8RsMssZNclWy0sSK6s9zNh
wgrFcd7SrUQU5+/x93qqis3dCX3J/EoYRA3+V94vBceVLgSyOJIgQGa8Vjtt
hi9pphubC3SAfuK+4NM1VLiVs5DyygZAaH/SrmYSDe0fJxzeI22ECQP/OQse
UETLsBst/HkTHNub7ifFv0jC01LZ6NGV0njgy9qZmJN/OD+um9428pnlaFoI
2Z9pN4RVx8S/rrmvigfW/7C5EquBYfP5UQ5+VBw80Z9/abc6tNErVlVxNYAl
7qKa8loHpQO+Hg1aKwPcAj/PbR9UgeC5UP52PRM2G2hWXWMR0Mdg01sWnYSQ
6HpmdJUpxGu+axHOIeKzVQYk8ks9fPp8ec7BTGs47lw8WdNigA2ms3sOVTEx
VdlpKjDHBBrE5TSUZsgYuZYxOhyog2PzhJK/tZLQPp2tPLh/hpvWvWeT7/oV
qPjYyavhhQIkli8EXfkljLW5Rd/XLJfF2HLrnD+uxtjjVkc+fogMT+0/Suxd
4rUG919uHkseG2v9ws0uUB7ubngoYnFLHv5bXLdiIlYPgjXP680WKiB9g1Dk
WD4BgWE50EnRgoKVwZNZabJo23prcGWvPCbfWOY0UqoILhcLPiqfE0NVvnxN
kSZJ/G8QWV8DqOib8mHmU5YaePNckJ/IJMCIe25eugkTX56cESPOq8J4tkz2
QBEJMs3Zzq9v2cJIP5nfPp+OI3l5O+4Is/CZverpndVM+GHfW/B9uSaqv1p9
Lm+XJjZ0f34rYWgFj+Z8rtfp6GJBZoyIwkMqyiUfCL5aKQimim/mBzqeciaS
feOnpcc5fyKPv3OJp2DOxPUeM2k5UDGUfqKtRYCnB8Qj2wKsIVtR0uXaHV3s
F4h5fieAhtLbY2zeaXdwEkzGgw6fH+KCYV7oi8pqrizl5950c2P4dr/UeWJE
EymFybefWVGw8oru8ctsBZy77L0l8JYASLWvyipn/uLMX/lxvD1slGv6fbfB
fNYC9wVRlFyg85Zzg/VucUDMFCtbBp6E3CTB5t3ybROGZEhZNvjG6ZENNuW5
7F4nQ4d1RBlRlywjKAwhRvOZGGOv7YqvngnqMOZ66rPGZwr0FI7cHD9tC8kX
NqV8C2XgtSS/PfQOIyRrLN+wXPA3Z25ScPKJ4CTXd61xtw93lnN27Z69veJE
SPxlxtGo40PpkRIn5i1Z7P96nvM50RgKdxyUKPDRxI1s7/mpOR10OuHTYso2
RnKJ6bWBai3ovpffRNPRh7NpbqE5zgQwSdj0lx3Di+6+BbOVIlJYG+rAvqtu
BXcSVis3Cehj50GTU+opDGSc23SlVpgM96Kbe1ful0fFQYdd8UVq6KMyZnrs
lDK0D8y73eTwoFBjYV9ViQRaPJCcnOS3wZ4n6pv4SPqwvn/yrIyREcQ+Kma/
VVsB1wV7bOK28ODhgoW2qEvjXAOf6OwvbZYo8keLdLpDB8q6ePgeRhuCwOvA
zIk5JlpptoTe2qIJg5dbbSTnNYExE7xlRyUb5Ruk3diRWqDXt1/PgaINzRld
l9KiLJH75H2QsZ8edDa2unmzdSF6YvAdJwHA1bn2T14lFePFfCxj3QxR0rT0
ScplecgRKnw4uSCBrkePC3ofnOdaljya3+Y7yVG2DbFyExrkXDhgulC17yf3
0RbJncr+5nhNQnobr7I2uBMPpf3j6kL2XISiizkD725cSDlMJcLJx3VHN50j
QibPmRDB6yb4YuEqfyabCHKBalZTpjpw972Dya5uGqg1/83HXAU0rH4Z1WKr
iv9ddy4JVbDCyAe6o58ideHE7o5w1gFDUD8I8YLBliCrFEk92krBHbKBfppk
OoKAidKyT0awKoC+YdlbTbwrsO3+lKY27n0he254JROczibed96pjupSakk1
uQTcZWkZw66i4/qryiyh98qQRgpQ/rKFAF+t96/Z0mkFPe/izx08qY1mpWcq
dxyiY3pLx6zAGVusjtiQ5c0whP53dwoKuoxAofdLrf9PAzj4+7YY00IJdZZF
bRZkEFG3+55ATIgpGtgPb+mzJUFk4d41FxfJ0HFk1YGfHznwD9n/tnyjIins
XOQmPSYSCuuoiYnmSxzt+kon2ACS9fuP71zyOe3KjjrN1xZwhJPQsTLj//up
4UghG6C0eu8FC11LDA/P2Dc0TgbRvSFPiCH68PWGs8aaNWw8JiRwRVWADOtW
LQi98dMGuaIB+wAtI0h9b577i6WEr8Zn39dFauHyxGd6cdFsFC14uT6/TwXu
ft+YJaqhDb39VyOy7+vivze9uoYqihCe2WolEagChk0Syyz3iELuvtKWWqIY
Ug89DNpTMMwZr80LmHed4LzMvVhTZ8uHw6Of3vMpjHKlLjz+q+tsBW9o3mId
F/TweVHCotoqQ1y4HrEh/KYJFH3xX7ZCgYRt2fOXd8Xr4JF76vLURhoUjjEe
U9rVUW1ewe7nQQLmjcelfzewR6W5gVuRQ3QgG08ZWDqYAGv+u/mULgMCXULl
71sr4Ojt59UVOzVwva/JmWZVHbiw8gPtaowSrjHXPHP7hhr6Uzxc19R+4ngN
BHwNrxzj7G1zvrLCjQ/d2YJ9Y29M0DE8rycoXAtEs/2Mq6X14Lu9aIKVPBlF
yu+G5r2QBU9bkWc21fIweT73nLH6LFf4b9eB1HefOaydyXXGVS+5T5vqDNvl
rYGfKV0/nkjDzr0qog//MvFzKT3tRawoHs4cJFPchCFdijk/VPOPk/7dd8sq
ZTYwzQw65V1J2B2c9OG5jzY+IsZtu/pZBpONc9JETvDAgw/9kb9mxeC+pm83
/YEerj2WOi5IUYGz4rGTuS5EcC9mVDYDHTzl3h77WUfA3ApCxeMl7iYrs8ir
ee0xvKvurLULE6w3HLaXGGHDdNVKTvAQQFxKh4GmCRXr9zbk6NxlolxYq+Ly
VBM8PfLl1716Tfi6OiM9+6UuWIVTf+ZHA8Iewq4jLwzg/PylVnIxA3yP6zyp
3sTEhn9zJ+3ZqnCix+/mgTck6F7eeqTogC1696otlr6jww3+Awx+jhFEeomv
n7M0Q981pY9dl3xecbvdkU5/Xdj+vCJ6Sy8TEzeWB+5ulAORQx9WfPEiQdrZ
reqC4ySIVyYcNAgVQtr4wtlIljy+PZsfcp5jBaldZnmnA8nYZPcyoFiMjqa7
h6pb4/kAGZJlu1/woLih9T9I+MEN2cznPfuJCfEO2c/ffiNgnfQTyU8umvjk
xI8SbUcd5Na8yd98RBbylvM03+pQArj6WLF+zgDTG3WErV0U4bcy9ZTfc1Xg
3b94fOtDG0i9FCl586Qh3qxyc220ZeGj7JrPuZJ0iCPsWnnmoDreTvP12ClP
xM17HryLKLLBL9J7lG5togL36NXZb6kMeL2r6fzqVcY41mbOWlWoDac0zqzb
sYUCNcUvB9QzbMHxZWVMMcsQRb52+0fosZESmj/2TM4OT1/lO5hXQYeYTdWj
1+ONoXdqINfylBHcONRa5OmqgSknT9z6/xxVvsh6YDrFgZHJdOmOtVQ0Ctv2
+sV9Q5StNrYgT0jj4b18rsG5vZzGkD29Fg5SkNDstl/6kSLckNWQt6yY5a59
8TuQc4YP44I7PAPrAPv3CD4Y4uqD5vmeCwQjOgw6cnvKr1pDS1/UwAV/bYyM
zPAR86HjXbsSvvhiM0i0W7v4qJmAo5MLSoxIPaR6d7TGNdiCYj/VnAJL91Jc
an2DWZjf+pIxuVsJV4c2Mz4rLoNvlY6w5+RfjtLmYGevCRa+HOaVEExZ6o//
vCb9RklQycD20dwfnHj5nCpVQivX5OOJE0/tf3AimFEUFws6TsWdf6eXqQii
l/bTuN4EKPebbEpaD/jnfrcS7REV/BmySRdEGDDd4b/x52YJ9Dav4b2r+JND
NiAUUqYnOfopmzTOrNeBHZ+D42L9ZDExSr9zNUkJk9O6M4qX8pB0cEOz6lFF
UPmwiM8rlKFn+vjRG3JmUFhKFIrlJ6G5VLrm7rd6SF7dHaCiAzjC/vwzwJ4G
B1LfnPwnyYT6l8JGvIMKIOax3m7+qgBuGJwjtfHKo7nsPfFVBDkcHtZZy6PJ
B9Nl18ePfJSAluenpVauE4DNOU78/0r+cLMEvdVdWkSRbyebQJg1gZZdpR2/
4wnYl9l/TiyMiv89U5l27LCEv4fvv1/XRUGH1+7tTRVU/BrU/mbSxwquyren
/xOl4N2Tz+9FIw2/NM4LeucIw+aDL04WVv/jNsyEuadRZrjaPMXDV4TpOEEQ
+kjQ1gDvmYDVyQpEWNFRtql6ShI1u3RLdGQXOGWmJM83W/9xhmqMg4ov6yHP
vwsX0j0UIUrsSKrvLlXo0KveOjRkhIde93xXX0MCw/CtBrFkElCPTxpneVrA
yL58muRlbTx44Fn10Rl99KC37vH6bomOHi7bPt0gw/qyMwyjdAPYPL5u8OEI
HfMP+pRMfyBCdpHqsVd+GrBVagMnv5EOblo3PuawNJHXUH/2jA8BZQUzy82+
2uHtxaO6sYVMyCOuPeV0hg1Sw/tk3EfJcHhmS9XfH7Jo7sWvq8dcgfqhVw/0
vrJE/b9y5wyytOFYVZv6jX+G0BudZ2D7zBjG/e5t4xfWRKUbk87zS75x/Hi3
t8ioHYzvfnzrlzEDKS2RipUtLDxU/i18W6MReF3olo8N18TdTWzuM9TCqHkH
+YkYOsqP6n7uKVYHpYOdLg+cl3Lbjkfjiqw2zNJf6Xb5K+LTkrGxwXtKaDF9
gM+5QR//9r8Yk+FRh5j/8s+AIgkO6/R91j1qArHpEWnPU0j4MXvViVsrdHCh
js30nqBCUQBrysxYATmfyobjSeoot37FMqGbtnA2JF5heTUdCykOfefPGWF8
e3/7yrNMePtCnac+mYgNfZYXV82SUEs/lyzgKg01LsQWV78B7ud7BuHEjH7u
zIJhRpqTEXSuq/vNuqKGhhWUWPEILcxItqowISpBxpdOy2SiNJ7uflHhc0wG
r206EkQYNwe9nemkIGEKHj5yN9SpQx8lpz5f3GujAPsIT6VPxUxwrXW2Xz+e
xI9GyuvT4qpsIVPMTTIqhIE/pkVOTnuysZkupNE3YoIReZeciGFaoP7qjJjP
og40T2zIGD5nB0rPq0rlDzPwSn1+N43HBHOSXG9+WmSi8+C/RMuzqnDk28fB
vhIdSNH94Tn4E7Doel6EdjoNXhbd+6pVygDhkf1DZ3MVQclSltGzRhg9W0ps
DgjNccUiZTRf9whhlpzTlwCaBCQ6R+GjF785quUu+4R5bHC4fKVMcoQ+3J+o
vZPUyYC+JLeD3mwzyPnxiqFooIU/Vw+L1njS0En+2vC1J9Z4pvsiV/GaPgSJ
7zQ+P0yDRx9GHwdvtAC+wDU35h9r4VZCpeUuVwr+dnN3WZVlhd8i98uklWnB
sT50rl9657PjPEZ7G3Tg6J4/Mj9WKWGvXL2X2DlVnIv9c/+XyEdO/3dsMzL4
znWk+YRJ70PuxURBwTbrIY7AiQ99ZO+vnJpwUiln/De3Ud2joHSHAmqk94Rv
mOCDwRuuP7bULIO+GMOmK016+Ne1d+ZcnTz0xvRuqQ8kwqrnnWZ12iZwdk2S
mdQPMpJ239UQKKNgoKB7X8cHKlr6h/od/y0Ptj7TlYyHGnBdaeHA0GYrGFpX
K9virYfabCc5Fs0QN1/adzO6wQD5lD7KKSbJg4fCa/f0V4pA2UR+/YGljYvM
+Ove32Rhw6UXSmdd5OC2YuFCsa0ZVuSLO75M1IVp4yvuPUs+H+XmcfZtDhtT
9t0/8ktAC26pL7PTGSbDMzlTMxpTCXqei05edJfCcvGHOncKluZRX6H8lycL
JX5sLv4jSoLErZ3aZyO0oZz9UyCtnIYqTxuVr1oqgeifhz1PeJf8NZAsIFJk
js+FEzzXWmiDSFfzcHOjLrRtvjc4f9wA6gxM5XJ4ZbHocqG57B4lTAj/5XFQ
AnDzRctR8WO6UGFqden0NSY4rtMdTOy1w+WKdqk85kyY6cSNFeksIIu0PW93
tIFHu/YLNARTsSiqJNhjiXtsSLyNUcukMKYkbMff3TOcGv/ZbzF7Fzg1Lqfa
/DPN4Nbzxex7eloYVtMoQ3tHxZO2jSffRllheJjiCfpaPfj0iuc1RZkO1t+D
0jf81IdKq+AG1XoVTLTdok+LIOBrxuSp6KUcKNvdcO30STqWOIfsSBsxwoMU
NRFOMhNuRQf5WTYRsMC4TagxVBMlpR6M/+mzRLZQbOqnMQoUHp6qutFDg6JP
d/PDhOxwdcfFxF0bqJDopbz3pAsLgmMr/H8ZmUJ8C/P3dJH20h6GW4Sd1kEZ
CZ32id3aaIsu8YRjEjBQWWLSnEmAwEP7XvUc0wf2FkOypoo6siMzEvyeqmDb
zpFPGRH6+HJjzq1od0XwOz5WbUbUgNbzY5d/iWmC1JewZ65fefFveezxvc5S
aD0SVXF6QhH6g1Rv/p4VQT3LhZ8qfIvcxWUbX7tsYkOPi2n6llwiygaExV1f
yuMxXpnV+sFLPXQhekdeijjeVCc2ESplcd2ooUboEgfTH+dYnhxTg+qBLYVm
4kTo4nspY7HUL+uv2po+lySih9n5DalVipgr1UoLaTDHtrCvm78v9YkiPy+4
jOmC9OFjn8XP8cOTnferbPR+cPt/2zYWCc5wW66tV4FkFnaOTOpl9pKgxjri
0m1ZEqxTarbxcKbgs71Bo7s8peEVTiaTclRB8p86Uuxl8M9YVwHfhmUg6vFL
II1PCrhfHLtF9tvBl8PcwBAjOuofFR1VF2fh56j9CWaSZmB5QV1B768mHktI
DvCS0Ef7vIgr2xnyYPfW3f1hqwDy+4VOz03xY+Lt07cdvXQhbF1UCsVaES+r
/D3gtJaACcyRkl8tNNhLvYtZkop4rOr8wfWRRMyt6ZtsX2BD7V56hv+YNgr8
6RUm9ephQpb434cfbGFz2p9g4Ut05HlfKrp/lomr98kvG/UjQHta+NhqQ2Fc
171D8u8ZaTwyyjl/rMkM5qZK3Q7UE7GdcDjB+DYVX5AO7SVNMvGq0kaBG0ZE
WCu09VrWDAnKeJRGv99p5khHf3ZpGBzhmjw+JrWDPc29qpGVwrvUpzXiMgum
EsoQzvmuTFn6z+YrabXVsUpYe/eqyp07AvAm6aG1yjcBaDTcEV9tYYyvM3sf
NYWToWvVa+07Z7Wh1cehLDXZDu2d99roOf4/Z5sj+FVZsHlNUL+ogDl4ftqu
1H6UjG0XYiYPS+qjYEeTqtkzAtpc95166yQK3Wsd+JK6RSFA0b57FYkF/XGx
yfe6CKi2O+DNxpsULCSOg8qCMWrJzJno2JDhqyUlbUcDGShuz+up28Qw3Og2
oSlfCApyK4/IUCVBf/FZ+nyTJYSJNrNm4/RQIOhFtWcRDW/pfH9zUJ+GPn/u
TVKfqcC/v+XntzarQ39+/dudgnY4aij9+OTXJf/4o7ZCMZcF684e3Jz51wIk
xr/vi7DQRX1P0Va2nD6uY2UqTOjZAhb/C+Qk0vHbtymvH11GGFFdeYVlQYAf
X9fRbNb/5nae3iSYHCWFRpwTkTuy6aCgQ+/eNa6I6iFzEst2E3GffkD5rSXv
SKJlOsSqqGBfXXFe8SVtLG03Nx/TMcZqBgysfqsNGZNf3r+ro0CsUHhFZJMQ
TDrvrXe3meGu7xA1WfjIi9nRbs9i/W1ReFXZ3qA+KpxlRJQYeS5xxvDqSnF1
MnyUG5vnXyWHJj7GVjYZqlj150bLCzDB5EHJKqdwEny4z9h4foIMHqUteVor
zLGy5Hwg7tKBZ04l0vaheuC+Sp/0ttgS3LddJM6f1MXyoyU/HpvS0NncSLHp
ny5mpvLZWVxTAZdb20wj6Eqw96XxPV8JG1BwNbCV8aBj/0DZ80hnBv4PSRlJ
/g==
"];
fit = ResourceFunction["LineFit"][pts];
Graphics3D[{Point[pts], Red, Thick, fit}]](https://www.wolframcloud.com/obj/resourcesystem/images/0d2/0d2a067c-c8a8-4862-a551-3e7b756a3b08/270c7814298b4fa5.png)
|
| Out[3]= |
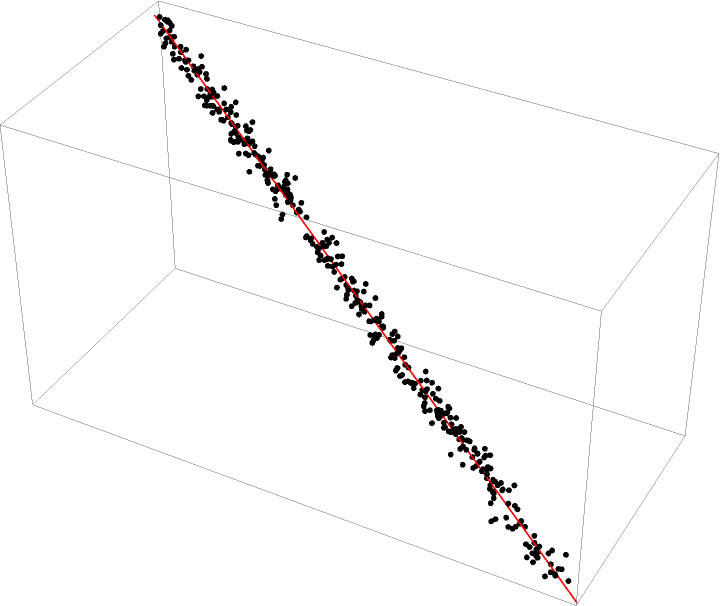
|
Get a Dataset with all the fitting details:
| In[4]:= |
![pts = CompressedData["
1:eJwVl3c8FP4fx83MZO9x5xyHc+7Onc29jaT4UqiMVGREklGRKFJmaEoZZRSh
Uho03LslGYWsSqjQQoVKMn5+f33++fzxeXwe7/fr9XwS/Xe5BfLx8PAc4+Xh
4V86s1zO31beyoY9Ee+SeGOIeDlOpD3UTRtvPS2U6DphB7+0zfZfG6XhniR1
TzFxFi4HC4WaIRWkeN9UMHLhAYernAuiLZLwSvWyzjJnC3Czr0z5/omMLKdt
HwSu6GNnhtUBnccAfCW9TzaOGOJq4pOpcGsmGo2FDSWM2WHctn/D1yMY4BEs
NUepMQaGvJbIyAV1PHfa61i4oAjcsTzl1FcsBFVjXWmlfmy0MV/fKhJGBHHn
jwwpGy2I8QcBGKdDRlimdBJRAwvayx2HKrUwb3rFNkKWEYoI+9Fa1pFh6M+Y
jGOyOvh7r+71i9FDS+oXI83vInBrjxD9lacq2J3fp8xjZAsTaZ1z8lsYqP7U
ythgkoUUA0/qYp0+Dn2Tp41GqUD8tv3vijapgF9UIBYDExN4Xjk4XCUAZcGu
6DedDIW+nhfjDtJRX/RYZ1+3GmydTr21Zg0RLldxo0I3kiCUvJWQGiuLqe89
D7Mj5HB4XjH2p5ARfFh5L9F/BxGDXpCCREs0UW+tZJuyJxvqArLiym4TcfNE
NkfQQxvHGJFNUrt00XR/N4lF14CyzT0PD3tpgoeG7YnGJAvA/PqLxgNaeG0+
xXW6nYpeltnWGleYcLP21p3vy4lo7DUdqreMjCf/+zgXFWmH7769z3xaTwfL
qaFJBssETuZOy6elyQJr5f7afZLCaKzT+av9rQxWpV8x3phqD4mJ79nXD9Hw
xDHagQ4tFuZNqqRuz2fC5J+nA9G7NNC/2+PqU3cy3h6uyDopaA8tZ+oVr9cy
kNQTFj1yi41vH47e/YWm8NxIv8W7TwsfqlbEpwrpY9YbwQvRsRxor2ht/Jmn
jRmt/kNHqDSMS3Ys+jPMA4meX3RFoy9xHzd6Xdd4L4gSFHkNlUhLlGy0tD0w
QwYyN89VM98AHG2bCs995sP72/XYsVmvOMY3Unlrz/3kjJTmOnzdZAv3Kskh
UtcNkbjzlfZApBFubayMkAg2xemHecNJblogdi73/EitHkjVZg94HVCGd8Wn
D33rXeRquF+Xf78ojpXlV9sv8dviprHdoc0TNIhQeUM97WQEQpGT+ZXFy3HZ
IV87GfIPzqWDFT9cIwRgW4MVf56CPfLdPfQjpIkOgSfUVOd4jOHksc5t2uWm
2EMvfyegQQFxheY/RlM6IF/z86b4fnsIz9i9pt2ciQPdUtmS0WzUO0JpVTTm
h1CudcyvA484R9/MDr0THuI+bY5ePDVji6EFBp88hOkQ6jFd89KEBVuj9u1s
NbLFOv0rpr29NHBefa12rSoThH1y60J2KYGYp/GgxlVB3Dl7R+HCY2ncVHS7
R/q1MfTn1Hs+J5Hw08xkkHa7Dh55xRFhZltBgZix3ksdfTwoOSzt60dHBYKX
Z2WdFRJTCxy7e7Uh7XeMq3AGFSY/ZH1QmWOg18Ca6ZexBMhRfStVEUwEL56o
K2+OaMOEmj65DqTR6pdXPHuZPPpaPM4h7yFD1qot0o9GFLDsa8tUVb0kep9K
PdE/aosS/wWtWwijwnSeZrzlOAvUvP16bt82wY3Nwyt37SDCCuEZbfXduqAE
pvxpQjY49GuqdMqKCt70w3brTtJB/sGUfH2FGTLkqz+c3U2GXkXFlQEONJD2
DNGtqyeA4HX5EpaAMA4XefDG7JPBzLHdbnfdSfCPwdJPviuHDZmzBXrm8mj7
WrlTtNMCfbQcVx9eS4FVf7Tmz0fqg7JK8HmTZYB7yyyoU8pUePi20vJcKwOK
iArLZYKtcNhO7a4VTReOG8WtCowxhJ8afZxfl/WhOMEgc6e+ElYIX8hWatNA
c0dH3LGDjW3fovdazhDg5nHlaJlzOsDXKc9JKqbD5lvb3fy+KOPtZ6+597OV
sFGjpDzpqD72put8G16jBud6W7pS6lVhUSzhmIOPCZwtKGo61qmF0vSMvpU/
abhGYqjAf4MxKpQ9+1L0hABOibVEmSxdcC1cPaS3kR/vpl2iCJsJgBt1Rd+O
sz84whUH4sUotniFd9O2k+P6sL1rIOvYfSbIpNX+uShFwpZiEb4ePTlYZJuf
Zo7LwKvP7GmnH2zUduuLm0vThOQNJsVrjujA9ELkc5ckQJ7JWtoTDTqEBd0d
CSEbgePywJW+n/TQI6BUIUBBDihVzCGzT5LwL3atNu95W7g6PZoeY0vHuDDn
0jE9Nm6djLrW7GCDjwp3DJ/TosFmlemRR0eZMNX7LUOpwRzOOdn4Oq7Uxhvz
HA/5fCranRloLzIyhpUC9p8piZpov1vZLJVPGx/oDO05HcFGd9sMIUoxCWxy
PX/K52nDDpqdX9ttEvRZPjpqOCWDtR6Xk1PPyaGD78fn9Bg2HOj84BsfS8Lt
yxb7r6uRMfrnNnHLVjscsbl56oEeA9oasHxdqxE0DfssdwoRBsaKI+2m60c5
tgmvV992FEZhtTfaocFSeNg9uC57SBRyiruAVSIFtye7UjIS7eGy//NDK/Yz
0IppcfvaaxZWhWVeCzW2gsXVW9ap3dBFjcgh414HOoa3btTvOKUE8fd093/S
4EG6VfPjD/7LUfPG1/esq/pornVtnYG+ItxOeFXvzCLAH4Wun7bxonjj98oG
nn0zHLP7jxacjkxwSvs86U65Zqj2oNl1dlIH7KtFB8beGYCxN6/iXJkFCu3x
RoUWLVhGYFXxXKZBELOEWKXNAqtufaOdnurIOs0fMxagg9XKtR+TY81R5g3l
BkNUB76cp5gvLtJgY+j0Z+L6Lq71F4N7aSW1nIj0OOrHy+3cvJQmn5Z4c9gT
efDwnuVL+Z8d/kmvVhfPB8/o2e5aDnz+aesani1ym2NckSLHi00LQcJsHsAd
HtGyro6GoGk1NfLqylJfbYvourTdGq35Vp0eeKwHoBIZHBXHgGyqg7Rjlx1u
ueleJZtDh8taMxZd/7FBQFL9085Aa+QN8XW9hxS46T5gu96EBm09cdWcnxZY
WpPSM+ipDdNuNXBJjgEOjYMBoXlvOQH2+e+KH7zi+ApJbtyZOsG5i+Ojn35L
o7ZCckrqPz5w5H/EHHAWg7L9BmkWqWPcx8Wb63fEjnAqF1eoeC1/z7m0Zdcu
qzKA8A8RJ2yoVKzTUbe030rHbln7YsqMBe6t+Sv41ogKm2SNiygrl/Z8pSJP
sA8TxKtnjYsJRKyW+SbwJkwTOzTbJC4S6Bj/2OWXerUCvNxse7pYnQRl7z/z
7xfXB2tH1TbqTiKWJqUobLdXRNMvJ8u6iiQx7uxx21Ouo1yNshxCtYUIKGQa
Bf4qsof0sWOeH0foGJgpWbDCkY2jpYqpF6IscFkfpNy1W8pp/zv+9UNUMPzd
m985YgJr6ZAcYEtCA5vluTVBOugbrLAvodEYrQ0fbt9poAeeg8MMKQNdmA8J
a44VI+Dz9veXLGz44c+/rFqrrRKg4WS9zrXXFvzfvTiyH+lovUEw/+gSX/Xw
PEF/eXt0T9m3bUMRHdRmw/Y9rmTB3SLVpFYnHbhKL7owzS+J0QFdP32s1HFt
6xTtx6gRnD4c9OjLb020MK6puSlNRD9JKfO1sSuhLrE0RC+TiWcd4x+st2Tj
79cHzFUUjIHy4dmN6QtaGOLYd0KLQ8aUJLuhjk1M8LaJHJ+ZJ6HTaNHTz6+1
sFb5zoZcMEWTd61nOohkECP8FxslRoGVzuucFealcWrj48pX2SKQn7mvNl1I
HATvXs7R4LfGS/1T5xXOa8GpublRIwc6bN2yWJCwnA99NhYIPsr9zD3rP1fx
SVUSli/cuzR+hIYNcyXsMrYCzLgOjovEqAPT0MGfzqeL7z/JdVqcUIARlexM
M2V1CP7wH8+2Pbxosv+SgvqJAU5UYemd+kw++Jy04tz4ISp4epY/7C/RwIW/
Rcffxyij9BnJF/trFKGI00tr3MuPEy53ahKnBXC2bJ47yWXCBoNrG41SFNDF
YsXurmda2NjY8O5Npj3MD514ltjGREOpmq+8F1koWLZl3C3CCjdu++K3T10H
til6X96xgQYbAj5OvcvQgl+nX/7eniWFRcvCrNf3yiK75IZa/5cfnL/+wbPz
L79xJzSNIxu7lqE1ZeCVwbAN5naGHefjpcMRFef9XnUMsL5kHt65iYFdMRWG
JlvVgORb6HxogQC2DxfWXxFkwZn0rcP/6jXx8Po4jswIGQUe659ZS7WFkj7N
4wtsGr6NZLF5ppl4jS8ugCfNDF50/f1wJkEHBatCCh5ZUtGpIeuGA5GJfAQP
1fFIEjAvfza8Iq0N3e1xd0ZmLVGd735xRbg+3JpNk4uqMoBqTVYhiTjF9Vzx
p7OsrosTVPTf+OWMV5xevzspu9cYw5NSYVaqhSbOfreIv+KlhTlh5dYBfDZw
ic8lfWcZFZvTclab/2CgLWdtoN5xXXQW7fuQqSgBl7RSktZypOFs3DV2WakW
1iVd9AoUloOb2cKeK16rQvLPT2r1aXRolDISpc8RsMssZNclWy0sSK6s9zNh
wgrFcd7SrUQU5+/x93qqis3dCX3J/EoYRA3+V94vBceVLgSyOJIgQGa8Vjtt
hi9pphubC3SAfuK+4NM1VLiVs5DyygZAaH/SrmYSDe0fJxzeI22ECQP/OQse
UETLsBst/HkTHNub7ifFv0jC01LZ6NGV0njgy9qZmJN/OD+um9428pnlaFoI
2Z9pN4RVx8S/rrmvigfW/7C5EquBYfP5UQ5+VBw80Z9/abc6tNErVlVxNYAl
7qKa8loHpQO+Hg1aKwPcAj/PbR9UgeC5UP52PRM2G2hWXWMR0Mdg01sWnYSQ
6HpmdJUpxGu+axHOIeKzVQYk8ks9fPp8ec7BTGs47lw8WdNigA2ms3sOVTEx
VdlpKjDHBBrE5TSUZsgYuZYxOhyog2PzhJK/tZLQPp2tPLh/hpvWvWeT7/oV
qPjYyavhhQIkli8EXfkljLW5Rd/XLJfF2HLrnD+uxtjjVkc+fogMT+0/Suxd
4rUG919uHkseG2v9ws0uUB7ubngoYnFLHv5bXLdiIlYPgjXP680WKiB9g1Dk
WD4BgWE50EnRgoKVwZNZabJo23prcGWvPCbfWOY0UqoILhcLPiqfE0NVvnxN
kSZJ/G8QWV8DqOib8mHmU5YaePNckJ/IJMCIe25eugkTX56cESPOq8J4tkz2
QBEJMs3Zzq9v2cJIP5nfPp+OI3l5O+4Is/CZverpndVM+GHfW/B9uSaqv1p9
Lm+XJjZ0f34rYWgFj+Z8rtfp6GJBZoyIwkMqyiUfCL5aKQimim/mBzqeciaS
feOnpcc5fyKPv3OJp2DOxPUeM2k5UDGUfqKtRYCnB8Qj2wKsIVtR0uXaHV3s
F4h5fieAhtLbY2zeaXdwEkzGgw6fH+KCYV7oi8pqrizl5950c2P4dr/UeWJE
EymFybefWVGw8oru8ctsBZy77L0l8JYASLWvyipn/uLMX/lxvD1slGv6fbfB
fNYC9wVRlFyg85Zzg/VucUDMFCtbBp6E3CTB5t3ybROGZEhZNvjG6ZENNuW5
7F4nQ4d1RBlRlywjKAwhRvOZGGOv7YqvngnqMOZ66rPGZwr0FI7cHD9tC8kX
NqV8C2XgtSS/PfQOIyRrLN+wXPA3Z25ScPKJ4CTXd61xtw93lnN27Z69veJE
SPxlxtGo40PpkRIn5i1Z7P96nvM50RgKdxyUKPDRxI1s7/mpOR10OuHTYso2
RnKJ6bWBai3ovpffRNPRh7NpbqE5zgQwSdj0lx3Di+6+BbOVIlJYG+rAvqtu
BXcSVis3Cehj50GTU+opDGSc23SlVpgM96Kbe1ful0fFQYdd8UVq6KMyZnrs
lDK0D8y73eTwoFBjYV9ViQRaPJCcnOS3wZ4n6pv4SPqwvn/yrIyREcQ+Kma/
VVsB1wV7bOK28ODhgoW2qEvjXAOf6OwvbZYo8keLdLpDB8q6ePgeRhuCwOvA
zIk5JlpptoTe2qIJg5dbbSTnNYExE7xlRyUb5Ruk3diRWqDXt1/PgaINzRld
l9KiLJH75H2QsZ8edDa2unmzdSF6YvAdJwHA1bn2T14lFePFfCxj3QxR0rT0
ScplecgRKnw4uSCBrkePC3ofnOdaljya3+Y7yVG2DbFyExrkXDhgulC17yf3
0RbJncr+5nhNQnobr7I2uBMPpf3j6kL2XISiizkD725cSDlMJcLJx3VHN50j
QibPmRDB6yb4YuEqfyabCHKBalZTpjpw972Dya5uGqg1/83HXAU0rH4Z1WKr
iv9ddy4JVbDCyAe6o58ideHE7o5w1gFDUD8I8YLBliCrFEk92krBHbKBfppk
OoKAidKyT0awKoC+YdlbTbwrsO3+lKY27n0he254JROczibed96pjupSakk1
uQTcZWkZw66i4/qryiyh98qQRgpQ/rKFAF+t96/Z0mkFPe/izx08qY1mpWcq
dxyiY3pLx6zAGVusjtiQ5c0whP53dwoKuoxAofdLrf9PAzj4+7YY00IJdZZF
bRZkEFG3+55ATIgpGtgPb+mzJUFk4d41FxfJ0HFk1YGfHznwD9n/tnyjIins
XOQmPSYSCuuoiYnmSxzt+kon2ACS9fuP71zyOe3KjjrN1xZwhJPQsTLj//up
4UghG6C0eu8FC11LDA/P2Dc0TgbRvSFPiCH68PWGs8aaNWw8JiRwRVWADOtW
LQi98dMGuaIB+wAtI0h9b577i6WEr8Zn39dFauHyxGd6cdFsFC14uT6/TwXu
ft+YJaqhDb39VyOy7+vivze9uoYqihCe2WolEagChk0Syyz3iELuvtKWWqIY
Ug89DNpTMMwZr80LmHed4LzMvVhTZ8uHw6Of3vMpjHKlLjz+q+tsBW9o3mId
F/TweVHCotoqQ1y4HrEh/KYJFH3xX7ZCgYRt2fOXd8Xr4JF76vLURhoUjjEe
U9rVUW1ewe7nQQLmjcelfzewR6W5gVuRQ3QgG08ZWDqYAGv+u/mULgMCXULl
71sr4Ojt59UVOzVwva/JmWZVHbiw8gPtaowSrjHXPHP7hhr6Uzxc19R+4ngN
BHwNrxzj7G1zvrLCjQ/d2YJ9Y29M0DE8rycoXAtEs/2Mq6X14Lu9aIKVPBlF
yu+G5r2QBU9bkWc21fIweT73nLH6LFf4b9eB1HefOaydyXXGVS+5T5vqDNvl
rYGfKV0/nkjDzr0qog//MvFzKT3tRawoHs4cJFPchCFdijk/VPOPk/7dd8sq
ZTYwzQw65V1J2B2c9OG5jzY+IsZtu/pZBpONc9JETvDAgw/9kb9mxeC+pm83
/YEerj2WOi5IUYGz4rGTuS5EcC9mVDYDHTzl3h77WUfA3ApCxeMl7iYrs8ir
ee0xvKvurLULE6w3HLaXGGHDdNVKTvAQQFxKh4GmCRXr9zbk6NxlolxYq+Ly
VBM8PfLl1716Tfi6OiM9+6UuWIVTf+ZHA8Iewq4jLwzg/PylVnIxA3yP6zyp
3sTEhn9zJ+3ZqnCix+/mgTck6F7eeqTogC1696otlr6jww3+Awx+jhFEeomv
n7M0Q981pY9dl3xecbvdkU5/Xdj+vCJ6Sy8TEzeWB+5ulAORQx9WfPEiQdrZ
reqC4ySIVyYcNAgVQtr4wtlIljy+PZsfcp5jBaldZnmnA8nYZPcyoFiMjqa7
h6pb4/kAGZJlu1/woLih9T9I+MEN2cznPfuJCfEO2c/ffiNgnfQTyU8umvjk
xI8SbUcd5Na8yd98RBbylvM03+pQArj6WLF+zgDTG3WErV0U4bcy9ZTfc1Xg
3b94fOtDG0i9FCl586Qh3qxyc220ZeGj7JrPuZJ0iCPsWnnmoDreTvP12ClP
xM17HryLKLLBL9J7lG5togL36NXZb6kMeL2r6fzqVcY41mbOWlWoDac0zqzb
sYUCNcUvB9QzbMHxZWVMMcsQRb52+0fosZESmj/2TM4OT1/lO5hXQYeYTdWj
1+ONoXdqINfylBHcONRa5OmqgSknT9z6/xxVvsh6YDrFgZHJdOmOtVQ0Ctv2
+sV9Q5StNrYgT0jj4b18rsG5vZzGkD29Fg5SkNDstl/6kSLckNWQt6yY5a59
8TuQc4YP44I7PAPrAPv3CD4Y4uqD5vmeCwQjOgw6cnvKr1pDS1/UwAV/bYyM
zPAR86HjXbsSvvhiM0i0W7v4qJmAo5MLSoxIPaR6d7TGNdiCYj/VnAJL91Jc
an2DWZjf+pIxuVsJV4c2Mz4rLoNvlY6w5+RfjtLmYGevCRa+HOaVEExZ6o//
vCb9RklQycD20dwfnHj5nCpVQivX5OOJE0/tf3AimFEUFws6TsWdf6eXqQii
l/bTuN4EKPebbEpaD/jnfrcS7REV/BmySRdEGDDd4b/x52YJ9Dav4b2r+JND
NiAUUqYnOfopmzTOrNeBHZ+D42L9ZDExSr9zNUkJk9O6M4qX8pB0cEOz6lFF
UPmwiM8rlKFn+vjRG3JmUFhKFIrlJ6G5VLrm7rd6SF7dHaCiAzjC/vwzwJ4G
B1LfnPwnyYT6l8JGvIMKIOax3m7+qgBuGJwjtfHKo7nsPfFVBDkcHtZZy6PJ
B9Nl18ePfJSAluenpVauE4DNOU78/0r+cLMEvdVdWkSRbyebQJg1gZZdpR2/
4wnYl9l/TiyMiv89U5l27LCEv4fvv1/XRUGH1+7tTRVU/BrU/mbSxwquyren
/xOl4N2Tz+9FIw2/NM4LeucIw+aDL04WVv/jNsyEuadRZrjaPMXDV4TpOEEQ
+kjQ1gDvmYDVyQpEWNFRtql6ShI1u3RLdGQXOGWmJM83W/9xhmqMg4ov6yHP
vwsX0j0UIUrsSKrvLlXo0KveOjRkhIde93xXX0MCw/CtBrFkElCPTxpneVrA
yL58muRlbTx44Fn10Rl99KC37vH6bomOHi7bPt0gw/qyMwyjdAPYPL5u8OEI
HfMP+pRMfyBCdpHqsVd+GrBVagMnv5EOblo3PuawNJHXUH/2jA8BZQUzy82+
2uHtxaO6sYVMyCOuPeV0hg1Sw/tk3EfJcHhmS9XfH7Jo7sWvq8dcgfqhVw/0
vrJE/b9y5wyytOFYVZv6jX+G0BudZ2D7zBjG/e5t4xfWRKUbk87zS75x/Hi3
t8ioHYzvfnzrlzEDKS2RipUtLDxU/i18W6MReF3olo8N18TdTWzuM9TCqHkH
+YkYOsqP6n7uKVYHpYOdLg+cl3Lbjkfjiqw2zNJf6Xb5K+LTkrGxwXtKaDF9
gM+5QR//9r8Yk+FRh5j/8s+AIgkO6/R91j1qArHpEWnPU0j4MXvViVsrdHCh
js30nqBCUQBrysxYATmfyobjSeoot37FMqGbtnA2JF5heTUdCykOfefPGWF8
e3/7yrNMePtCnac+mYgNfZYXV82SUEs/lyzgKg01LsQWV78B7ud7BuHEjH7u
zIJhRpqTEXSuq/vNuqKGhhWUWPEILcxItqowISpBxpdOy2SiNJ7uflHhc0wG
r206EkQYNwe9nemkIGEKHj5yN9SpQx8lpz5f3GujAPsIT6VPxUxwrXW2Xz+e
xI9GyuvT4qpsIVPMTTIqhIE/pkVOTnuysZkupNE3YoIReZeciGFaoP7qjJjP
og40T2zIGD5nB0rPq0rlDzPwSn1+N43HBHOSXG9+WmSi8+C/RMuzqnDk28fB
vhIdSNH94Tn4E7Doel6EdjoNXhbd+6pVygDhkf1DZ3MVQclSltGzRhg9W0ps
DgjNccUiZTRf9whhlpzTlwCaBCQ6R+GjF785quUu+4R5bHC4fKVMcoQ+3J+o
vZPUyYC+JLeD3mwzyPnxiqFooIU/Vw+L1njS0En+2vC1J9Z4pvsiV/GaPgSJ
7zQ+P0yDRx9GHwdvtAC+wDU35h9r4VZCpeUuVwr+dnN3WZVlhd8i98uklWnB
sT50rl9657PjPEZ7G3Tg6J4/Mj9WKWGvXL2X2DlVnIv9c/+XyEdO/3dsMzL4
znWk+YRJ70PuxURBwTbrIY7AiQ99ZO+vnJpwUiln/De3Ud2joHSHAmqk94Rv
mOCDwRuuP7bULIO+GMOmK016+Ne1d+ZcnTz0xvRuqQ8kwqrnnWZ12iZwdk2S
mdQPMpJ239UQKKNgoKB7X8cHKlr6h/od/y0Ptj7TlYyHGnBdaeHA0GYrGFpX
K9virYfabCc5Fs0QN1/adzO6wQD5lD7KKSbJg4fCa/f0V4pA2UR+/YGljYvM
+Ove32Rhw6UXSmdd5OC2YuFCsa0ZVuSLO75M1IVp4yvuPUs+H+XmcfZtDhtT
9t0/8ktAC26pL7PTGSbDMzlTMxpTCXqei05edJfCcvGHOncKluZRX6H8lycL
JX5sLv4jSoLErZ3aZyO0oZz9UyCtnIYqTxuVr1oqgeifhz1PeJf8NZAsIFJk
js+FEzzXWmiDSFfzcHOjLrRtvjc4f9wA6gxM5XJ4ZbHocqG57B4lTAj/5XFQ
AnDzRctR8WO6UGFqden0NSY4rtMdTOy1w+WKdqk85kyY6cSNFeksIIu0PW93
tIFHu/YLNARTsSiqJNhjiXtsSLyNUcukMKYkbMff3TOcGv/ZbzF7Fzg1Lqfa
/DPN4Nbzxex7eloYVtMoQ3tHxZO2jSffRllheJjiCfpaPfj0iuc1RZkO1t+D
0jf81IdKq+AG1XoVTLTdok+LIOBrxuSp6KUcKNvdcO30STqWOIfsSBsxwoMU
NRFOMhNuRQf5WTYRsMC4TagxVBMlpR6M/+mzRLZQbOqnMQoUHp6qutFDg6JP
d/PDhOxwdcfFxF0bqJDopbz3pAsLgmMr/H8ZmUJ8C/P3dJH20h6GW4Sd1kEZ
CZ32id3aaIsu8YRjEjBQWWLSnEmAwEP7XvUc0wf2FkOypoo6siMzEvyeqmDb
zpFPGRH6+HJjzq1od0XwOz5WbUbUgNbzY5d/iWmC1JewZ65fefFveezxvc5S
aD0SVXF6QhH6g1Rv/p4VQT3LhZ8qfIvcxWUbX7tsYkOPi2n6llwiygaExV1f
yuMxXpnV+sFLPXQhekdeijjeVCc2ESplcd2ooUboEgfTH+dYnhxTg+qBLYVm
4kTo4nspY7HUL+uv2po+lySih9n5DalVipgr1UoLaTDHtrCvm78v9YkiPy+4
jOmC9OFjn8XP8cOTnferbPR+cPt/2zYWCc5wW66tV4FkFnaOTOpl9pKgxjri
0m1ZEqxTarbxcKbgs71Bo7s8peEVTiaTclRB8p86Uuxl8M9YVwHfhmUg6vFL
II1PCrhfHLtF9tvBl8PcwBAjOuofFR1VF2fh56j9CWaSZmB5QV1B768mHktI
DvCS0Ef7vIgr2xnyYPfW3f1hqwDy+4VOz03xY+Lt07cdvXQhbF1UCsVaES+r
/D3gtJaACcyRkl8tNNhLvYtZkop4rOr8wfWRRMyt6ZtsX2BD7V56hv+YNgr8
6RUm9ephQpb434cfbGFz2p9g4Ut05HlfKrp/lomr98kvG/UjQHta+NhqQ2Fc
171D8u8ZaTwyyjl/rMkM5qZK3Q7UE7GdcDjB+DYVX5AO7SVNMvGq0kaBG0ZE
WCu09VrWDAnKeJRGv99p5khHf3ZpGBzhmjw+JrWDPc29qpGVwrvUpzXiMgum
EsoQzvmuTFn6z+YrabXVsUpYe/eqyp07AvAm6aG1yjcBaDTcEV9tYYyvM3sf
NYWToWvVa+07Z7Wh1cehLDXZDu2d99roOf4/Z5sj+FVZsHlNUL+ogDl4ftqu
1H6UjG0XYiYPS+qjYEeTqtkzAtpc95166yQK3Wsd+JK6RSFA0b57FYkF/XGx
yfe6CKi2O+DNxpsULCSOg8qCMWrJzJno2JDhqyUlbUcDGShuz+up28Qw3Og2
oSlfCApyK4/IUCVBf/FZ+nyTJYSJNrNm4/RQIOhFtWcRDW/pfH9zUJ+GPn/u
TVKfqcC/v+XntzarQ39+/dudgnY4aij9+OTXJf/4o7ZCMZcF684e3Jz51wIk
xr/vi7DQRX1P0Va2nD6uY2UqTOjZAhb/C+Qk0vHbtymvH11GGFFdeYVlQYAf
X9fRbNb/5nae3iSYHCWFRpwTkTuy6aCgQ+/eNa6I6iFzEst2E3GffkD5rSXv
SKJlOsSqqGBfXXFe8SVtLG03Nx/TMcZqBgysfqsNGZNf3r+ro0CsUHhFZJMQ
TDrvrXe3meGu7xA1WfjIi9nRbs9i/W1ReFXZ3qA+KpxlRJQYeS5xxvDqSnF1
MnyUG5vnXyWHJj7GVjYZqlj150bLCzDB5EHJKqdwEny4z9h4foIMHqUteVor
zLGy5Hwg7tKBZ04l0vaheuC+Sp/0ttgS3LddJM6f1MXyoyU/HpvS0NncSLHp
ny5mpvLZWVxTAZdb20wj6Eqw96XxPV8JG1BwNbCV8aBj/0DZ80hnBv4PSRlJ
/g==
"];
Dataset[ResourceFunction["LineFit"][pts, "Association"]]](https://www.wolframcloud.com/obj/resourcesystem/images/0d2/0d2a067c-c8a8-4862-a551-3e7b756a3b08/0adb33b5631fa0ae.png)
|
| Out[4]= |

|
Compare the result of LineFit with the result of computing the orthogonal fit through the definition:
| In[5]:= |
![pts = CompressedData["
1:eJwVl3c8FP4fx83MZO9x5xyHc+7Onc29jaT4UqiMVGREklGRKFJmaEoZZRSh
Uho03LslGYWsSqjQQoVKMn5+f33++fzxeXwe7/fr9XwS/Xe5BfLx8PAc4+Xh
4V86s1zO31beyoY9Ee+SeGOIeDlOpD3UTRtvPS2U6DphB7+0zfZfG6XhniR1
TzFxFi4HC4WaIRWkeN9UMHLhAYernAuiLZLwSvWyzjJnC3Czr0z5/omMLKdt
HwSu6GNnhtUBnccAfCW9TzaOGOJq4pOpcGsmGo2FDSWM2WHctn/D1yMY4BEs
NUepMQaGvJbIyAV1PHfa61i4oAjcsTzl1FcsBFVjXWmlfmy0MV/fKhJGBHHn
jwwpGy2I8QcBGKdDRlimdBJRAwvayx2HKrUwb3rFNkKWEYoI+9Fa1pFh6M+Y
jGOyOvh7r+71i9FDS+oXI83vInBrjxD9lacq2J3fp8xjZAsTaZ1z8lsYqP7U
ythgkoUUA0/qYp0+Dn2Tp41GqUD8tv3vijapgF9UIBYDExN4Xjk4XCUAZcGu
6DedDIW+nhfjDtJRX/RYZ1+3GmydTr21Zg0RLldxo0I3kiCUvJWQGiuLqe89
D7Mj5HB4XjH2p5ARfFh5L9F/BxGDXpCCREs0UW+tZJuyJxvqArLiym4TcfNE
NkfQQxvHGJFNUrt00XR/N4lF14CyzT0PD3tpgoeG7YnGJAvA/PqLxgNaeG0+
xXW6nYpeltnWGleYcLP21p3vy4lo7DUdqreMjCf/+zgXFWmH7769z3xaTwfL
qaFJBssETuZOy6elyQJr5f7afZLCaKzT+av9rQxWpV8x3phqD4mJ79nXD9Hw
xDHagQ4tFuZNqqRuz2fC5J+nA9G7NNC/2+PqU3cy3h6uyDopaA8tZ+oVr9cy
kNQTFj1yi41vH47e/YWm8NxIv8W7TwsfqlbEpwrpY9YbwQvRsRxor2ht/Jmn
jRmt/kNHqDSMS3Ys+jPMA4meX3RFoy9xHzd6Xdd4L4gSFHkNlUhLlGy0tD0w
QwYyN89VM98AHG2bCs995sP72/XYsVmvOMY3Unlrz/3kjJTmOnzdZAv3Kskh
UtcNkbjzlfZApBFubayMkAg2xemHecNJblogdi73/EitHkjVZg94HVCGd8Wn
D33rXeRquF+Xf78ojpXlV9sv8dviprHdoc0TNIhQeUM97WQEQpGT+ZXFy3HZ
IV87GfIPzqWDFT9cIwRgW4MVf56CPfLdPfQjpIkOgSfUVOd4jOHksc5t2uWm
2EMvfyegQQFxheY/RlM6IF/z86b4fnsIz9i9pt2ciQPdUtmS0WzUO0JpVTTm
h1CudcyvA484R9/MDr0THuI+bY5ePDVji6EFBp88hOkQ6jFd89KEBVuj9u1s
NbLFOv0rpr29NHBefa12rSoThH1y60J2KYGYp/GgxlVB3Dl7R+HCY2ncVHS7
R/q1MfTn1Hs+J5Hw08xkkHa7Dh55xRFhZltBgZix3ksdfTwoOSzt60dHBYKX
Z2WdFRJTCxy7e7Uh7XeMq3AGFSY/ZH1QmWOg18Ca6ZexBMhRfStVEUwEL56o
K2+OaMOEmj65DqTR6pdXPHuZPPpaPM4h7yFD1qot0o9GFLDsa8tUVb0kep9K
PdE/aosS/wWtWwijwnSeZrzlOAvUvP16bt82wY3Nwyt37SDCCuEZbfXduqAE
pvxpQjY49GuqdMqKCt70w3brTtJB/sGUfH2FGTLkqz+c3U2GXkXFlQEONJD2
DNGtqyeA4HX5EpaAMA4XefDG7JPBzLHdbnfdSfCPwdJPviuHDZmzBXrm8mj7
WrlTtNMCfbQcVx9eS4FVf7Tmz0fqg7JK8HmTZYB7yyyoU8pUePi20vJcKwOK
iArLZYKtcNhO7a4VTReOG8WtCowxhJ8afZxfl/WhOMEgc6e+ElYIX8hWatNA
c0dH3LGDjW3fovdazhDg5nHlaJlzOsDXKc9JKqbD5lvb3fy+KOPtZ6+597OV
sFGjpDzpqD72put8G16jBud6W7pS6lVhUSzhmIOPCZwtKGo61qmF0vSMvpU/
abhGYqjAf4MxKpQ9+1L0hABOibVEmSxdcC1cPaS3kR/vpl2iCJsJgBt1Rd+O
sz84whUH4sUotniFd9O2k+P6sL1rIOvYfSbIpNX+uShFwpZiEb4ePTlYZJuf
Zo7LwKvP7GmnH2zUduuLm0vThOQNJsVrjujA9ELkc5ckQJ7JWtoTDTqEBd0d
CSEbgePywJW+n/TQI6BUIUBBDihVzCGzT5LwL3atNu95W7g6PZoeY0vHuDDn
0jE9Nm6djLrW7GCDjwp3DJ/TosFmlemRR0eZMNX7LUOpwRzOOdn4Oq7Uxhvz
HA/5fCranRloLzIyhpUC9p8piZpov1vZLJVPGx/oDO05HcFGd9sMIUoxCWxy
PX/K52nDDpqdX9ttEvRZPjpqOCWDtR6Xk1PPyaGD78fn9Bg2HOj84BsfS8Lt
yxb7r6uRMfrnNnHLVjscsbl56oEeA9oasHxdqxE0DfssdwoRBsaKI+2m60c5
tgmvV992FEZhtTfaocFSeNg9uC57SBRyiruAVSIFtye7UjIS7eGy//NDK/Yz
0IppcfvaaxZWhWVeCzW2gsXVW9ap3dBFjcgh414HOoa3btTvOKUE8fd093/S
4EG6VfPjD/7LUfPG1/esq/pornVtnYG+ItxOeFXvzCLAH4Wun7bxonjj98oG
nn0zHLP7jxacjkxwSvs86U65Zqj2oNl1dlIH7KtFB8beGYCxN6/iXJkFCu3x
RoUWLVhGYFXxXKZBELOEWKXNAqtufaOdnurIOs0fMxagg9XKtR+TY81R5g3l
BkNUB76cp5gvLtJgY+j0Z+L6Lq71F4N7aSW1nIj0OOrHy+3cvJQmn5Z4c9gT
efDwnuVL+Z8d/kmvVhfPB8/o2e5aDnz+aesani1ym2NckSLHi00LQcJsHsAd
HtGyro6GoGk1NfLqylJfbYvourTdGq35Vp0eeKwHoBIZHBXHgGyqg7Rjlx1u
ueleJZtDh8taMxZd/7FBQFL9085Aa+QN8XW9hxS46T5gu96EBm09cdWcnxZY
WpPSM+ipDdNuNXBJjgEOjYMBoXlvOQH2+e+KH7zi+ApJbtyZOsG5i+Ojn35L
o7ZCckrqPz5w5H/EHHAWg7L9BmkWqWPcx8Wb63fEjnAqF1eoeC1/z7m0Zdcu
qzKA8A8RJ2yoVKzTUbe030rHbln7YsqMBe6t+Sv41ogKm2SNiygrl/Z8pSJP
sA8TxKtnjYsJRKyW+SbwJkwTOzTbJC4S6Bj/2OWXerUCvNxse7pYnQRl7z/z
7xfXB2tH1TbqTiKWJqUobLdXRNMvJ8u6iiQx7uxx21Ouo1yNshxCtYUIKGQa
Bf4qsof0sWOeH0foGJgpWbDCkY2jpYqpF6IscFkfpNy1W8pp/zv+9UNUMPzd
m985YgJr6ZAcYEtCA5vluTVBOugbrLAvodEYrQ0fbt9poAeeg8MMKQNdmA8J
a44VI+Dz9veXLGz44c+/rFqrrRKg4WS9zrXXFvzfvTiyH+lovUEw/+gSX/Xw
PEF/eXt0T9m3bUMRHdRmw/Y9rmTB3SLVpFYnHbhKL7owzS+J0QFdP32s1HFt
6xTtx6gRnD4c9OjLb020MK6puSlNRD9JKfO1sSuhLrE0RC+TiWcd4x+st2Tj
79cHzFUUjIHy4dmN6QtaGOLYd0KLQ8aUJLuhjk1M8LaJHJ+ZJ6HTaNHTz6+1
sFb5zoZcMEWTd61nOohkECP8FxslRoGVzuucFealcWrj48pX2SKQn7mvNl1I
HATvXs7R4LfGS/1T5xXOa8GpublRIwc6bN2yWJCwnA99NhYIPsr9zD3rP1fx
SVUSli/cuzR+hIYNcyXsMrYCzLgOjovEqAPT0MGfzqeL7z/JdVqcUIARlexM
M2V1CP7wH8+2Pbxosv+SgvqJAU5UYemd+kw++Jy04tz4ISp4epY/7C/RwIW/
Rcffxyij9BnJF/trFKGI00tr3MuPEy53ahKnBXC2bJ47yWXCBoNrG41SFNDF
YsXurmda2NjY8O5Npj3MD514ltjGREOpmq+8F1koWLZl3C3CCjdu++K3T10H
til6X96xgQYbAj5OvcvQgl+nX/7eniWFRcvCrNf3yiK75IZa/5cfnL/+wbPz
L79xJzSNIxu7lqE1ZeCVwbAN5naGHefjpcMRFef9XnUMsL5kHt65iYFdMRWG
JlvVgORb6HxogQC2DxfWXxFkwZn0rcP/6jXx8Po4jswIGQUe659ZS7WFkj7N
4wtsGr6NZLF5ppl4jS8ugCfNDF50/f1wJkEHBatCCh5ZUtGpIeuGA5GJfAQP
1fFIEjAvfza8Iq0N3e1xd0ZmLVGd735xRbg+3JpNk4uqMoBqTVYhiTjF9Vzx
p7OsrosTVPTf+OWMV5xevzspu9cYw5NSYVaqhSbOfreIv+KlhTlh5dYBfDZw
ic8lfWcZFZvTclab/2CgLWdtoN5xXXQW7fuQqSgBl7RSktZypOFs3DV2WakW
1iVd9AoUloOb2cKeK16rQvLPT2r1aXRolDISpc8RsMssZNclWy0sSK6s9zNh
wgrFcd7SrUQU5+/x93qqis3dCX3J/EoYRA3+V94vBceVLgSyOJIgQGa8Vjtt
hi9pphubC3SAfuK+4NM1VLiVs5DyygZAaH/SrmYSDe0fJxzeI22ECQP/OQse
UETLsBst/HkTHNub7ifFv0jC01LZ6NGV0njgy9qZmJN/OD+um9428pnlaFoI
2Z9pN4RVx8S/rrmvigfW/7C5EquBYfP5UQ5+VBw80Z9/abc6tNErVlVxNYAl
7qKa8loHpQO+Hg1aKwPcAj/PbR9UgeC5UP52PRM2G2hWXWMR0Mdg01sWnYSQ
6HpmdJUpxGu+axHOIeKzVQYk8ks9fPp8ec7BTGs47lw8WdNigA2ms3sOVTEx
VdlpKjDHBBrE5TSUZsgYuZYxOhyog2PzhJK/tZLQPp2tPLh/hpvWvWeT7/oV
qPjYyavhhQIkli8EXfkljLW5Rd/XLJfF2HLrnD+uxtjjVkc+fogMT+0/Suxd
4rUG919uHkseG2v9ws0uUB7ubngoYnFLHv5bXLdiIlYPgjXP680WKiB9g1Dk
WD4BgWE50EnRgoKVwZNZabJo23prcGWvPCbfWOY0UqoILhcLPiqfE0NVvnxN
kSZJ/G8QWV8DqOib8mHmU5YaePNckJ/IJMCIe25eugkTX56cESPOq8J4tkz2
QBEJMs3Zzq9v2cJIP5nfPp+OI3l5O+4Is/CZverpndVM+GHfW/B9uSaqv1p9
Lm+XJjZ0f34rYWgFj+Z8rtfp6GJBZoyIwkMqyiUfCL5aKQimim/mBzqeciaS
feOnpcc5fyKPv3OJp2DOxPUeM2k5UDGUfqKtRYCnB8Qj2wKsIVtR0uXaHV3s
F4h5fieAhtLbY2zeaXdwEkzGgw6fH+KCYV7oi8pqrizl5950c2P4dr/UeWJE
EymFybefWVGw8oru8ctsBZy77L0l8JYASLWvyipn/uLMX/lxvD1slGv6fbfB
fNYC9wVRlFyg85Zzg/VucUDMFCtbBp6E3CTB5t3ybROGZEhZNvjG6ZENNuW5
7F4nQ4d1RBlRlywjKAwhRvOZGGOv7YqvngnqMOZ66rPGZwr0FI7cHD9tC8kX
NqV8C2XgtSS/PfQOIyRrLN+wXPA3Z25ScPKJ4CTXd61xtw93lnN27Z69veJE
SPxlxtGo40PpkRIn5i1Z7P96nvM50RgKdxyUKPDRxI1s7/mpOR10OuHTYso2
RnKJ6bWBai3ovpffRNPRh7NpbqE5zgQwSdj0lx3Di+6+BbOVIlJYG+rAvqtu
BXcSVis3Cehj50GTU+opDGSc23SlVpgM96Kbe1ful0fFQYdd8UVq6KMyZnrs
lDK0D8y73eTwoFBjYV9ViQRaPJCcnOS3wZ4n6pv4SPqwvn/yrIyREcQ+Kma/
VVsB1wV7bOK28ODhgoW2qEvjXAOf6OwvbZYo8keLdLpDB8q6ePgeRhuCwOvA
zIk5JlpptoTe2qIJg5dbbSTnNYExE7xlRyUb5Ruk3diRWqDXt1/PgaINzRld
l9KiLJH75H2QsZ8edDa2unmzdSF6YvAdJwHA1bn2T14lFePFfCxj3QxR0rT0
ScplecgRKnw4uSCBrkePC3ofnOdaljya3+Y7yVG2DbFyExrkXDhgulC17yf3
0RbJncr+5nhNQnobr7I2uBMPpf3j6kL2XISiizkD725cSDlMJcLJx3VHN50j
QibPmRDB6yb4YuEqfyabCHKBalZTpjpw972Dya5uGqg1/83HXAU0rH4Z1WKr
iv9ddy4JVbDCyAe6o58ideHE7o5w1gFDUD8I8YLBliCrFEk92krBHbKBfppk
OoKAidKyT0awKoC+YdlbTbwrsO3+lKY27n0he254JROczibed96pjupSakk1
uQTcZWkZw66i4/qryiyh98qQRgpQ/rKFAF+t96/Z0mkFPe/izx08qY1mpWcq
dxyiY3pLx6zAGVusjtiQ5c0whP53dwoKuoxAofdLrf9PAzj4+7YY00IJdZZF
bRZkEFG3+55ATIgpGtgPb+mzJUFk4d41FxfJ0HFk1YGfHznwD9n/tnyjIins
XOQmPSYSCuuoiYnmSxzt+kon2ACS9fuP71zyOe3KjjrN1xZwhJPQsTLj//up
4UghG6C0eu8FC11LDA/P2Dc0TgbRvSFPiCH68PWGs8aaNWw8JiRwRVWADOtW
LQi98dMGuaIB+wAtI0h9b577i6WEr8Zn39dFauHyxGd6cdFsFC14uT6/TwXu
ft+YJaqhDb39VyOy7+vivze9uoYqihCe2WolEagChk0Syyz3iELuvtKWWqIY
Ug89DNpTMMwZr80LmHed4LzMvVhTZ8uHw6Of3vMpjHKlLjz+q+tsBW9o3mId
F/TweVHCotoqQ1y4HrEh/KYJFH3xX7ZCgYRt2fOXd8Xr4JF76vLURhoUjjEe
U9rVUW1ewe7nQQLmjcelfzewR6W5gVuRQ3QgG08ZWDqYAGv+u/mULgMCXULl
71sr4Ojt59UVOzVwva/JmWZVHbiw8gPtaowSrjHXPHP7hhr6Uzxc19R+4ngN
BHwNrxzj7G1zvrLCjQ/d2YJ9Y29M0DE8rycoXAtEs/2Mq6X14Lu9aIKVPBlF
yu+G5r2QBU9bkWc21fIweT73nLH6LFf4b9eB1HefOaydyXXGVS+5T5vqDNvl
rYGfKV0/nkjDzr0qog//MvFzKT3tRawoHs4cJFPchCFdijk/VPOPk/7dd8sq
ZTYwzQw65V1J2B2c9OG5jzY+IsZtu/pZBpONc9JETvDAgw/9kb9mxeC+pm83
/YEerj2WOi5IUYGz4rGTuS5EcC9mVDYDHTzl3h77WUfA3ApCxeMl7iYrs8ir
ee0xvKvurLULE6w3HLaXGGHDdNVKTvAQQFxKh4GmCRXr9zbk6NxlolxYq+Ly
VBM8PfLl1716Tfi6OiM9+6UuWIVTf+ZHA8Iewq4jLwzg/PylVnIxA3yP6zyp
3sTEhn9zJ+3ZqnCix+/mgTck6F7eeqTogC1696otlr6jww3+Awx+jhFEeomv
n7M0Q981pY9dl3xecbvdkU5/Xdj+vCJ6Sy8TEzeWB+5ulAORQx9WfPEiQdrZ
reqC4ySIVyYcNAgVQtr4wtlIljy+PZsfcp5jBaldZnmnA8nYZPcyoFiMjqa7
h6pb4/kAGZJlu1/woLih9T9I+MEN2cznPfuJCfEO2c/ffiNgnfQTyU8umvjk
xI8SbUcd5Na8yd98RBbylvM03+pQArj6WLF+zgDTG3WErV0U4bcy9ZTfc1Xg
3b94fOtDG0i9FCl586Qh3qxyc220ZeGj7JrPuZJ0iCPsWnnmoDreTvP12ClP
xM17HryLKLLBL9J7lG5togL36NXZb6kMeL2r6fzqVcY41mbOWlWoDac0zqzb
sYUCNcUvB9QzbMHxZWVMMcsQRb52+0fosZESmj/2TM4OT1/lO5hXQYeYTdWj
1+ONoXdqINfylBHcONRa5OmqgSknT9z6/xxVvsh6YDrFgZHJdOmOtVQ0Ctv2
+sV9Q5StNrYgT0jj4b18rsG5vZzGkD29Fg5SkNDstl/6kSLckNWQt6yY5a59
8TuQc4YP44I7PAPrAPv3CD4Y4uqD5vmeCwQjOgw6cnvKr1pDS1/UwAV/bYyM
zPAR86HjXbsSvvhiM0i0W7v4qJmAo5MLSoxIPaR6d7TGNdiCYj/VnAJL91Jc
an2DWZjf+pIxuVsJV4c2Mz4rLoNvlY6w5+RfjtLmYGevCRa+HOaVEExZ6o//
vCb9RklQycD20dwfnHj5nCpVQivX5OOJE0/tf3AimFEUFws6TsWdf6eXqQii
l/bTuN4EKPebbEpaD/jnfrcS7REV/BmySRdEGDDd4b/x52YJ9Dav4b2r+JND
NiAUUqYnOfopmzTOrNeBHZ+D42L9ZDExSr9zNUkJk9O6M4qX8pB0cEOz6lFF
UPmwiM8rlKFn+vjRG3JmUFhKFIrlJ6G5VLrm7rd6SF7dHaCiAzjC/vwzwJ4G
B1LfnPwnyYT6l8JGvIMKIOax3m7+qgBuGJwjtfHKo7nsPfFVBDkcHtZZy6PJ
B9Nl18ePfJSAluenpVauE4DNOU78/0r+cLMEvdVdWkSRbyebQJg1gZZdpR2/
4wnYl9l/TiyMiv89U5l27LCEv4fvv1/XRUGH1+7tTRVU/BrU/mbSxwquyren
/xOl4N2Tz+9FIw2/NM4LeucIw+aDL04WVv/jNsyEuadRZrjaPMXDV4TpOEEQ
+kjQ1gDvmYDVyQpEWNFRtql6ShI1u3RLdGQXOGWmJM83W/9xhmqMg4ov6yHP
vwsX0j0UIUrsSKrvLlXo0KveOjRkhIde93xXX0MCw/CtBrFkElCPTxpneVrA
yL58muRlbTx44Fn10Rl99KC37vH6bomOHi7bPt0gw/qyMwyjdAPYPL5u8OEI
HfMP+pRMfyBCdpHqsVd+GrBVagMnv5EOblo3PuawNJHXUH/2jA8BZQUzy82+
2uHtxaO6sYVMyCOuPeV0hg1Sw/tk3EfJcHhmS9XfH7Jo7sWvq8dcgfqhVw/0
vrJE/b9y5wyytOFYVZv6jX+G0BudZ2D7zBjG/e5t4xfWRKUbk87zS75x/Hi3
t8ioHYzvfnzrlzEDKS2RipUtLDxU/i18W6MReF3olo8N18TdTWzuM9TCqHkH
+YkYOsqP6n7uKVYHpYOdLg+cl3Lbjkfjiqw2zNJf6Xb5K+LTkrGxwXtKaDF9
gM+5QR//9r8Yk+FRh5j/8s+AIgkO6/R91j1qArHpEWnPU0j4MXvViVsrdHCh
js30nqBCUQBrysxYATmfyobjSeoot37FMqGbtnA2JF5heTUdCykOfefPGWF8
e3/7yrNMePtCnac+mYgNfZYXV82SUEs/lyzgKg01LsQWV78B7ud7BuHEjH7u
zIJhRpqTEXSuq/vNuqKGhhWUWPEILcxItqowISpBxpdOy2SiNJ7uflHhc0wG
r206EkQYNwe9nemkIGEKHj5yN9SpQx8lpz5f3GujAPsIT6VPxUxwrXW2Xz+e
xI9GyuvT4qpsIVPMTTIqhIE/pkVOTnuysZkupNE3YoIReZeciGFaoP7qjJjP
og40T2zIGD5nB0rPq0rlDzPwSn1+N43HBHOSXG9+WmSi8+C/RMuzqnDk28fB
vhIdSNH94Tn4E7Doel6EdjoNXhbd+6pVygDhkf1DZ3MVQclSltGzRhg9W0ps
DgjNccUiZTRf9whhlpzTlwCaBCQ6R+GjF785quUu+4R5bHC4fKVMcoQ+3J+o
vZPUyYC+JLeD3mwzyPnxiqFooIU/Vw+L1njS0En+2vC1J9Z4pvsiV/GaPgSJ
7zQ+P0yDRx9GHwdvtAC+wDU35h9r4VZCpeUuVwr+dnN3WZVlhd8i98uklWnB
sT50rl9657PjPEZ7G3Tg6J4/Mj9WKWGvXL2X2DlVnIv9c/+XyEdO/3dsMzL4
znWk+YRJ70PuxURBwTbrIY7AiQ99ZO+vnJpwUiln/De3Ud2joHSHAmqk94Rv
mOCDwRuuP7bULIO+GMOmK016+Ne1d+ZcnTz0xvRuqQ8kwqrnnWZ12iZwdk2S
mdQPMpJ239UQKKNgoKB7X8cHKlr6h/od/y0Ptj7TlYyHGnBdaeHA0GYrGFpX
K9virYfabCc5Fs0QN1/adzO6wQD5lD7KKSbJg4fCa/f0V4pA2UR+/YGljYvM
+Ove32Rhw6UXSmdd5OC2YuFCsa0ZVuSLO75M1IVp4yvuPUs+H+XmcfZtDhtT
9t0/8ktAC26pL7PTGSbDMzlTMxpTCXqei05edJfCcvGHOncKluZRX6H8lycL
JX5sLv4jSoLErZ3aZyO0oZz9UyCtnIYqTxuVr1oqgeifhz1PeJf8NZAsIFJk
js+FEzzXWmiDSFfzcHOjLrRtvjc4f9wA6gxM5XJ4ZbHocqG57B4lTAj/5XFQ
AnDzRctR8WO6UGFqden0NSY4rtMdTOy1w+WKdqk85kyY6cSNFeksIIu0PW93
tIFHu/YLNARTsSiqJNhjiXtsSLyNUcukMKYkbMff3TOcGv/ZbzF7Fzg1Lqfa
/DPN4Nbzxex7eloYVtMoQ3tHxZO2jSffRllheJjiCfpaPfj0iuc1RZkO1t+D
0jf81IdKq+AG1XoVTLTdok+LIOBrxuSp6KUcKNvdcO30STqWOIfsSBsxwoMU
NRFOMhNuRQf5WTYRsMC4TagxVBMlpR6M/+mzRLZQbOqnMQoUHp6qutFDg6JP
d/PDhOxwdcfFxF0bqJDopbz3pAsLgmMr/H8ZmUJ8C/P3dJH20h6GW4Sd1kEZ
CZ32id3aaIsu8YRjEjBQWWLSnEmAwEP7XvUc0wf2FkOypoo6siMzEvyeqmDb
zpFPGRH6+HJjzq1od0XwOz5WbUbUgNbzY5d/iWmC1JewZ65fefFveezxvc5S
aD0SVXF6QhH6g1Rv/p4VQT3LhZ8qfIvcxWUbX7tsYkOPi2n6llwiygaExV1f
yuMxXpnV+sFLPXQhekdeijjeVCc2ESplcd2ooUboEgfTH+dYnhxTg+qBLYVm
4kTo4nspY7HUL+uv2po+lySih9n5DalVipgr1UoLaTDHtrCvm78v9YkiPy+4
jOmC9OFjn8XP8cOTnferbPR+cPt/2zYWCc5wW66tV4FkFnaOTOpl9pKgxjri
0m1ZEqxTarbxcKbgs71Bo7s8peEVTiaTclRB8p86Uuxl8M9YVwHfhmUg6vFL
II1PCrhfHLtF9tvBl8PcwBAjOuofFR1VF2fh56j9CWaSZmB5QV1B768mHktI
DvCS0Ef7vIgr2xnyYPfW3f1hqwDy+4VOz03xY+Lt07cdvXQhbF1UCsVaES+r
/D3gtJaACcyRkl8tNNhLvYtZkop4rOr8wfWRRMyt6ZtsX2BD7V56hv+YNgr8
6RUm9ephQpb434cfbGFz2p9g4Ut05HlfKrp/lomr98kvG/UjQHta+NhqQ2Fc
171D8u8ZaTwyyjl/rMkM5qZK3Q7UE7GdcDjB+DYVX5AO7SVNMvGq0kaBG0ZE
WCu09VrWDAnKeJRGv99p5khHf3ZpGBzhmjw+JrWDPc29qpGVwrvUpzXiMgum
EsoQzvmuTFn6z+YrabXVsUpYe/eqyp07AvAm6aG1yjcBaDTcEV9tYYyvM3sf
NYWToWvVa+07Z7Wh1cehLDXZDu2d99roOf4/Z5sj+FVZsHlNUL+ogDl4ftqu
1H6UjG0XYiYPS+qjYEeTqtkzAtpc95166yQK3Wsd+JK6RSFA0b57FYkF/XGx
yfe6CKi2O+DNxpsULCSOg8qCMWrJzJno2JDhqyUlbUcDGShuz+up28Qw3Og2
oSlfCApyK4/IUCVBf/FZ+nyTJYSJNrNm4/RQIOhFtWcRDW/pfH9zUJ+GPn/u
TVKfqcC/v+XntzarQ39+/dudgnY4aij9+OTXJf/4o7ZCMZcF684e3Jz51wIk
xr/vi7DQRX1P0Va2nD6uY2UqTOjZAhb/C+Qk0vHbtymvH11GGFFdeYVlQYAf
X9fRbNb/5nae3iSYHCWFRpwTkTuy6aCgQ+/eNa6I6iFzEst2E3GffkD5rSXv
SKJlOsSqqGBfXXFe8SVtLG03Nx/TMcZqBgysfqsNGZNf3r+ro0CsUHhFZJMQ
TDrvrXe3meGu7xA1WfjIi9nRbs9i/W1ReFXZ3qA+KpxlRJQYeS5xxvDqSnF1
MnyUG5vnXyWHJj7GVjYZqlj150bLCzDB5EHJKqdwEny4z9h4foIMHqUteVor
zLGy5Hwg7tKBZ04l0vaheuC+Sp/0ttgS3LddJM6f1MXyoyU/HpvS0NncSLHp
ny5mpvLZWVxTAZdb20wj6Eqw96XxPV8JG1BwNbCV8aBj/0DZ80hnBv4PSRlJ
/g==
"];
fit1 = ResourceFunction["LineFit"][pts];
fit2 = InfiniteLine @@ Partition[
NArgMin[Total[
RegionDistance[
InfiniteLine[{px, py, pz}, {vx, vy, vz}], #]^2 & /@ pts], {px, py, pz, vx, vy, vz}], 3];](https://www.wolframcloud.com/obj/resourcesystem/images/0d2/0d2a067c-c8a8-4862-a551-3e7b756a3b08/28bbbd1685db49b5.png)
|
| In[6]:= |
|
| Out[6]= |
|
| In[7]:= |
|
| Out[7]= |
|
The one-argument case of LineFit is equivalent to the resource function OrthogonalLineFit:
| In[8]:= |
![pts = CompressedData["
1:eJwVl3cgFY7XxmUL2VtcXOu6xnWneY+dIpJUkqREafgpviF7FC0atGyiSSpZ
dY9VGqQks5KyKiI74vX+df4+5zznOZ9HzfeImx83FxdX6iourv+vB7a+sohJ
m+aM8/3OzPcY4ni+m+yLCZMGO/5ksb10WdT9FHP+Cb8hvvtTzT43ygTz4ImA
72/qOEnrhyI4YVxo3t8RVi4tAcbvi6IsvNRQMtp25+9LJCz/j/RC3YUJN+QS
Eu106fhOEj0eylqDVktUWsx/hngv16shimoKtt31aooMZXCXCPi2VEBAj6xp
ieB5fQSuxnt5tUzoyP5FrnPWhUm3+C/Z2sZ4LCRdXewkEUM8Qg79mqDA2qEz
nWrGEnjgRMirqBwCDDgdIboMk5BLkVB8Ip4B56M3Tfqn0TFoYj7i2V2AQvfu
Cv5fRHRIkhOeTzaCO7Eth5PshTBotOIulkhDT6sc8wqvLgZqC23L2kUDZSG3
K+rFDKweknZsj7SGnn/Tz8qfC8PYrM2o7/k1aPaK5HfMfy3eCPGpe3tWB1r/
t26r2QV1kLFbxho7I3yQesihxZ6ADMPHDv/F6gK5sWRmtNsYP8rxbieuB9jS
6Zl/4Kwe/CmKyftlycKrWsfyroIEHmWz1utvIMDp2wXy15y48O3E2VdyKtKw
+87n6SOGfFCb4CVfv3OIczlu/dexBhZ+493B5Z5oB+WLuzVEhci4oNxzzi+e
CceC6bvHaDzw5zN5eTZcAYvCLCK0h0zQUS0297imLTw3JU9HLBIh3jRcq0+E
jhKmGm8GF4jgtVUgZDLLCFcNbsdAPk0ksfnqj2tSwXKhTiPnOhFP6BdciCgx
Ar82hYTgSl0MT438cj6NBqvdYkQjRX6yS7+Y1+XofuTE1crP2943BJt91s9I
TSx0KN9V41RthLPr64RKcs0hL64otXUbN574skcxuUUBTEWPmn+8ugquTPld
Me5ZjSfPLTgkXtUGM4JAVxKJht+u2Zd576Dgce/FgmwKwGShkEShsAzsoLfd
bPQnYMGu6yMxXVpQFbHxl8oBKjZbUP5sVxGH9F7/Td22yigfmpGV0EVFGiuj
bb+5NYjXJRyWSBWFzg5Rk01pyqjiteCi93SRs/QwmPR4NTcQ6OwXBz1o+GhU
sbyBDPBlz49PA39lMOt3+f3FSUUYU4ka9CAKA5Exd1JTVRD/tp1Vkx4nws6M
ysn7lUbYvM09TtdXA/G02dHmcwYgGNp4al01A2XV/Sx3ZNrAuF/tn3BlQRiv
+H5ji6MUBvD+Z3t3WBy/Nw63F/4WAH1erudXf3Oh8L6P8h84MtCPL7J2P9bF
bdEV95CXBpL0euGMCxOcuWabahAVALF3OdnqgTp4Ze6BFUvLGBT6ybsvF4mC
suLPG3vLZbBBpCVUWJ6OuwJ1XYu5Ad6VKa0dztaD88bunRQGA6Nutqvt8qBg
ocV200hfc2CGwsBCujQIp0aMW3cp41XbT8eOrTfEHUJWQs6+LOiL3RP9Rl4R
YhrmHuXMEXENZftVH3VtMCC9HODkGyHV+9CPvRsMsPRp4hbtShNollAN8DCl
4o26fyeK7Kxh4ejL6t2nydBld3SifIGJiQ+maYQsIdxePEo+P6EEt49L3bGP
VcOcgORbpHN6MFaXVdFaoATnyh+5b+zRwcisEb5d+VRsFUyReGsB0JL37G1w
Bxk1Lxs83GhCB9tPlIMOkopo7WR6Y3uFFrxP6rgr5KYMdWNPTP5mquMk4Vyg
0xlFUMlcYk+raOI1JcvyTgkhUJGieJl4CGGwIsOo3VgTRP1pW0vHjPBxiEp/
2Kg+yk30nE4vY8COw8PP/roTMO6bXrRjjz6I751tv6z1lR35VrAqrX+WE1bC
vm+rawAvA4Vp9RtX9H9VXq5DjQTZJtn6eSNUbAq/zi9krY7Xb8Y2/RajQl6u
VH1xjRbusTjWMMDLgKDxu0v1/dqoKN8wYLJAhbm5cx9TDJUw+5V5jOw8CTym
J5k+lw3AUckZ/euZuMdfUEbkCgEWD+2jaj8h4YEn3jsjDpJR5tbwukuqTHjJ
H1ZzYbchHmrzYhY8ZcKAaeJluW4NSH/33fzigCGebrpPL/QXBiPl6p+pnyTR
lSvhbpmFLPC20G5WyauhU92fjOyvTKR3+ug36NhC2H7CwIcgEvi2idz8FcnA
seyy/c2+wuhdh5rfvsuDhrCd/9uPVCQdvkKh6FpB+91rL1+SDbGsItW+V98U
ZEaVO531idB5OMGYnE/GtC5p1ZphA5SK3Jfl9cYU+qSTLITf0XHqU+qeeIoV
SDQlPBxa2W9OWvDii9OmcGcXQesInwaetQ8ROvtYD3qvvMS9rfzI8hfkrdYR
A/vD4t5Nlaq47uFHj1gzXXDqaN18NpiBf5+V7hUcswXVxVmF93wiGKNqdcRW
RgLCCh53KGRLg6Llnvg9jkSMWNi7f0GdBA+KZq7wdNHRzCn1seUUC61kb38I
bLSFKwrthnXyNLycfxy6+K2gzdF35HiQDgyC57vOszRsLU5xw5X7LsotLmmz
VkSLmpA54+hpjqJCspTvWgm4/35+QeSeFo6+cLMVCl3Zf6ZWbMLIV3bp2gr/
17R3HPlGTda2UQFwCw2OjL0gj9I5+vpbHbVQSLqtb8cnI9jC2SYs3qYOC6ve
ufLpUfBXf15thwUDeRzdFGTLbOBxqndMXIgRSv6kv13QNINR2aSW7Zu50bqw
6q+0nSA0+V8aOaXPwmD9z6NH/ljDYV7T5IyPBuBKmg+lnGGi5YnO4eVnSljf
vIrfo04PYtpCBDeXK+HB+xuapzp1oNRhVGPxPAkd5i5vOcumQs5TVVk5sVUY
PZM1MC8iBQf/M1FWWEuAh509Iz+3k7Gn0Pt+6h4iZP4uHdIqM0LZ0ef/+77G
EIyHLyrG6zPxlHOE6qdjfBAwE6oWJCCKz2UO+YZ2E7GmwuX6tgoKBMZ6ML3D
DSClpefijRoaPmdJEni20LFmu2r9O1uAwWepLhpHlKCu/1f58z3q+MFXRs7n
jSbY2HIlemZSUHGDbm5TDwW+jO2TNg81wWPjw6rOKhTsuO5yfJW0CdgFLIhT
h6jIczM4jlcM4J+iLKf47AQnxXlBaHnDP3Zks9k1q990rEClgqCV/1OV70qg
BEhjas6mE9usFWC8WiNts4g2KPZNqM8S6NhZJjuF4mKQ2WJQxaJI40V73h2J
Ihr4da/CxEI6BW789tQJ3KWDk+FLJtq0Fb9aW3BJ7Rcd6z8HbmOVW8OzAuev
R3q/sw2F/isx5x7hnNJ5L1N1n4k3c7ZWCsnZAHm30+PSJ9LAYtIuix9TQs92
no5XOquwl5TmWKekAimz+Smqtavh0Jm6Ea5EcRQY1gz9V68LA+HUuKpHK30c
lxydq9OCMt6jw7tcjfGRY226SzIVS13rKYLnrIBvUSg7W9wA9l+fHXa4zEKb
63Mdl3sn2OdmNEMjdcc51hyeWU+XKY5jWXtf7TpROPXlfiCMaeKGjrOoKWEI
5nuUz7VGK+FOmT3cRbv1oGS3sF97vwZavRlV3H6cAtv+jpSdktXCfAmiddUQ
BS7V/rXU0frJwSn/dHHpJk5YT8Nxp0uyINUSvIXUrIF1JDV9+1MiIFNxt3W9
vArec2h59q5JFsLFpFO/nFDFPw3EykoCDZOsJrvvelmCc5wlw0CGhXcbVZc9
c2xAobR2QiNfAjWGplItG9UAKhncTwYNUUjr6ITAgCnsiUjvnd/FxH32cj0O
AraQXON0RVl7gXPj0Sc+wyBBiBrVfjUTQMKo176nptgsIPHXBJR6GOHwg6mc
X9xmoORJy6nM58XScpJKibwCuG4rHLu7ol/xRIE7j9so8FyRFNznycL1GXnL
eQxrMDTyKsO+FR64q7/ou2wDH0KzDaPuk4EkdKemLYqJOZXG++8JceOjWwP0
wO38MJ8aHPeSTceoLPPs+EwrmJ2a+kxc4b+3KbMHKCO2YCv8JJGmRIa4aq3h
e3F0fKZB3qW5j4hL3478KkYjYNVKZ9tZ6oOYGFdEmB4Ln4SfvpthIg6Rohcq
P8erYcMU+c+lIQ1UfO57cA1LD2iJDg4/tBXQuuLA9K8TGnBneZ9+V8rKfNN3
D/h/sYLWbQGvuq8pAudH+saXQVoY0CqhNuFJQ0WnvQQbfjYM1g6osmZpuMvG
SeGPvTX4BPyXY5UmCU4au5RGfinjMREDpUNVylgodVWkJ5kIh9bZPt+awUKS
QR9J/KgteB1/9PR8hAA0pZocZi3w47P84C1f/qlAkKGVdgCXHja6xL++pqeP
++vNvrFnzeDbg/GLNreM8GU+rdkrwwyefKfl17nqIe9QCnuKzgR7e10ugqwE
3soQ7FedIEDq2xGJwEIiHjwy3B60mgq1jsEMD2V+HHEe73dRUwS5YbXlvbpU
PBGQn6FGYsP6LJ/p+jQa3vJDLC+2Aq3nYZ0CQ8rAp7OlPzNbA4Pur/NpeK+I
p3064rPiNcE8fY2b79vX7LnIcHeWKz+umXz3uNhXEpMKD8ztEJYCRc2H4Txb
9EH2YGyX1wILW0daLz6+R4bgzIIwA38G1gUXb9uUR4Ciz5b648m6+ErWfIPj
AzU4bxPtqOhGxnUzmwz979KQOVP2oOcqgML0yJF7K9wuzWqa+S1oAeOuD8rh
jg5U0vT8Di9Rcd9u3jgzs0UOrcnvzIL9F86SwPj4uVW8yEpd2xiqwg0jjOSl
mzWqKOXc9r72piFYtSSs7gnWAKYjK670tjFGkqzbdVzVgWpTPhGcZYDrn+yl
3TmmgwH29slmZ4wh9FdQ1KdNEpj5WvSrdggBtuRapu91k0VzJ78qXg8NCOIe
XXijoAJCG9XPrxc1wKWGMRF1MSpqdS5atb23AFf3iM7JVmMcahLf5pRvBuEi
pg0umpLIolo1SKsoQqPWyIDfqBpO32+842hEh+9Zydz73NWAsfQtQz6IjOLX
owO4npJhkJqbU9DKwHt+dlWPZ3WhkVymZLfMxA8n+y+6RRnAQQVBEwdVFhrV
PVq1rpiOBQEPuuRjAFyKS8ut8sVh8pV/tRZbHWUax4PFVWUx+G3a9YrHK3Nc
7Xl7+b0pejWSPic62cELCYGA5geqwNgfLn7fnozIZ7lq37o5do/PX1q45xC7
GGoK+5LkcXFnWkGMhCY0JrYKHXWXxKvJb82VdksBq+Ns3au9RtDfHfvio5kJ
epCiE6cUZHFTXHmEqLAGpEgKO59W1sTssI0aoy0UqFDOCcw9S8RvCpzBL0QK
BHk8ftLewEQTF9SQc7aBvET+VdFgjI07jijZEwG+7ZEyeWWgib3uE8XFlsbw
bYfmGtdJA7xwUaX0TQYT/hwK4Ca/5gYDPCfNxyWOH9V5vNNOr+hT6YvdJ3cl
MHD5vf90oyTMEBbybA8Qkf+m+aXyFEmQrJhReROggdcUWCX/zsnCrJhXbrG+
NnYJNKzdbG2I57ZZrF9dyoAm3i+57Ztfc4gu2u1m8Qtsl6mpU/Mr/++nVn52
QxUZwiIYm+R7NHHkx76MiVVUWJ3hG9povgrOXV7X2pLNixXm5Vx1gg3slyTt
ZCvdCU6LUuafdjFFrA0x/qn+TAPubXkVVraSD9StFK6W1hlCfun9il2riZj8
dP5I2x0K+MxIZW4YYWF89Od20Uo7SBDY6+mtSkSboabTE9VGUJi0vqx0uw76
DLr93HeQBq53QAokNUEyf8OzhEP6eGv9OYPVp9VxyfUFsegaGZQ9qkQTYqWh
dswRYwXVsDD9XepFAQImMYR4DITIkHSXELq1jAeTptIM8rQE4KzW75f3/hHQ
/l/W8gtvMqiaxjD6TmrDpubWb91Txrh6A4FOX/ErY8p/1cshK3p33VHEP2eA
psuvrkXJmkDvMzGBpEtE3N9l51J+wQg+U3IiyWspoDczf6r5Ewvpvz7cu2/G
wGt793N09lkB1fE7z+lIIjRatKhtuKaHr8OHvBUipfDnuHOOzkkCTAtRlnx3
9HHIB7VLvm/mhyt3Ym0EA2XA/s+1I5LHFVby9deNj9az8E6Naa8ixRYsymob
LmyUwU+MQ84ir9fCTRlPj//4tGGzz/uL03009F59+qh4ly7ujHf+EDtMAU0/
G5ZcrxIMuM9cYgART16M5/JapuK2V1IbvkpZwT09ow/CRFU89IFVINilDztZ
l0rXNOqChYpR7GTACs9t9l10FWJi9txq3rPJ1mDMfcgdxSl4TNLhfneEOcSd
VFJYY8TEt3/H9KwbrcF2oV7h/LwcPF279bCXiSbSJgMuTvIJ4XBp7ZmnsTJg
666zm3fYFIsbWld1/ljh9UGidW7aGnT28xSW+K0E8cdcJhIfakOgnk9OPIOK
Gz1JJUvBmniif8lv4pQxVC/8+9Mhb4qV070vQ7vtQHB/9JXbR8ko0fVeaG8K
A/IPTgrF7yKjx0b9lFsnmNAcX65Ek19irxbe+d43SgbN3lscNl7JF72SASlT
7eJgczz1fK6GANz41FhzsJgfNS0Ux/f8XWI3i1Ycun1bELdWMrSCHXRAt+fo
s/50Gn6puH5WK5eGzgmHvx+pt4KEAw+83x82hCVJ7kpIZKK70eLvJDEybPb7
XtLOYOH5kCyXOfoMmyvD5GZR8B/2lYaaes5OVSyqehrZQNCGb/23v1YZKYDC
VRNmWxgBZQy1ooWjxfBJagJXSaQCqPFGxyVmKMCjF17icmpElLQ/8TVshowl
fIXLktUsYDiqu0hL0zC5k6f1Y5IlTNzy3TLbrA4/dxSX/CdKxRTFA/bt+Xpg
uJcvfm4VDUtOuoeOkYwwYHfNw5t6FtBh+/DG2LQx8hzdHy58CsDtsFuA/hoN
vJrxQXKjKhUK9z/9nveSiYn51dsX19tC7taQNo8pEzy+cKqv1dwO7PSFPL8v
z7L/l/LjgJWWCL5X5OZ9Ovb/fqbpIllLh62nlku/ehmif0y+YtBxU9j6b8ad
ZGOMLfs6j/E5mcGL+aKj21/pocQGrm7qNQZQt+UfusRPgB/vLa03zRvix6Oa
fcIhCxyfvWfIbdytbI21k118O9XhVtxPwcEbBljsXaDRvr2bnbyKy2nDLxEU
iRbreWenAHa9H8JUldTwekqfSKUzDd+5Ee9veWoFb+M9F72tDTDEtlutPYcJ
tYb19EOZ2jB66/kZZXMG1r9YT6/pMEbfQPtl+Wo26Oc51B9114GJ63e7dAap
+MHoSHLS6F92nd+vnQ7+PGgU7TJetPyCfW/TnRM8btLoI6J/vPf5DDtjWOTN
SN4yZzW1ceB1kSwYiHMNhCioY4tOp5iXuQFSPMUjiktYwCNvH6h9noAvHmqf
GDc1grpTLep6BTzgcLPm+lMxbjTnyt2qfpcAAXi1UfyFLubXJzzdRDSCdV4B
fOaZTLQdGmqNvaiN1dnt7i2JVLggkbmLKCGDoYFNe+r5teB/v4sva9SpQ6NM
hcYZfgpSFeeH8YkMBrn8nY9kqEGKbEF/zZgUDHoXhf/crIb7q/7nmOpOwgje
v5fUgxiQmrZ5R0rsHHvdix8tm68vcqJSCqn3crSxlP9csUwXHdQOt02qzhOQ
4N+60/KFLlibW2k6XCHixqKikBFPKmiujS9Jysplb7viPfp49DMbtTV2RvRP
cw5+SiT8ZvPB97dRC7xXqej7gb0jSs8Ges1MuSUDtZB/zenF2ItUWMO+WFe1
SRc3OacIZc2z4MBw6Za4f0ykrWku5Am0g7c3N51uKJSEXiYxceL3WkwfZIRm
ujGwum28u+qFNYjlqHYOFGhjt03j0bGjLKjPd34SFmAIemoH1awLGag5KHxK
w1EMr1T2v67+owyiCz/HBw2FoVll94ZKH3HM4aS6mN7Rx1B7AidJkwnr/4Zt
WmerDhV2lz90baCgr171xwUBOrZ+lnvrcMYKBDTYONKugHVBn46MryHC/FBT
h90NBhZFz9Z0kG2h26ydafdAB9qUfsuaH1nxi7GQmKGuabb4pEpPodI7ztek
oKVHCwYwGWgzGB5ggn2Zl8yfe8pizIyPz9URIkRFy2ZclhaHp/e8AumGCtjX
oGYrUSKO9MgYck2LBnR/DpQxfW0EBUq+fTwhTKzSmDrRlspE+tVRx1+fbKB9
S5Bg/h1DYOelq0fQTZCkOv1qc7IR5tkn2jPdzIB0LNVt12o5TO90S6iPJ8K7
bOncxAl1EH7ILf4jzBh5/81re12g4Mt1SXwnlMzAKd61xewJCQZXLXbXxlPx
5BnXK1RFVRx9O/aQUEaEbx2TM2nmarCZh2nMn2uEng+Hx4lyVFS+fbPpdjob
GnoTpprkGHi6qncQf1rD/wHgXZIn
"];
fit1 = ResourceFunction["LineFit"][pts];
fit2 = ResourceFunction["OrthogonalLineFit"][pts];](https://www.wolframcloud.com/obj/resourcesystem/images/0d2/0d2a067c-c8a8-4862-a551-3e7b756a3b08/7cf242bd383e1da7.png)
|
| In[9]:= |
|
| Out[9]= |
|
| In[10]:= |
|
| Out[10]= |
|
All points have to be numeric:
| In[11]:= |
|
| Out[11]= |
|
All points have to be in the same dimension:
| In[12]:= |
|
| Out[12]= |
|
Real numbers have to be used:
| In[13]:= |
|
| Out[13]= |
|
Do a fit in 10D:
| In[14]:= |
![SeedRandom[1234];
n = 10;
m = 200;
a = Normalize[RandomVariate[NormalDistribution[], n]];
t = RandomVariate[NormalDistribution[0, 10], m];
pts = # a & /@ t;
pts += RandomVariate[NormalDistribution[0, 1], {m, n}];
ResourceFunction["LineFit"][pts, "Association"]](https://www.wolframcloud.com/obj/resourcesystem/images/0d2/0d2a067c-c8a8-4862-a551-3e7b756a3b08/46c1c24fd518a91a.png)
|
| Out[14]= |

|
This work is licensed under a Creative Commons Attribution 4.0 International License