Basic Examples (3)
Display the electron-dot symbol for carbon:
Display the electron-dot symbol for carbon as Text:
Show the Lewis formula for arsenide anion:
Show the Lewis formula for arsenide anion as Text:
Generate the Lewis formula for chlorine-37:
Generate the Lewis formula for chlorine-37 as Text:
Options (10)
Alignment (1)
Adjust the alignment of unpaired electrons:
AtomColor (1)
Change the default atomic symbol color:
DotColor (1)
Change the default electron dot color:
DotPlacement (1)
Specify the placement of unpaired electrons:
ElectronFilliing (2)
Lewis symbols predated quantum mechanics by over 20 years, so the default results for He may surprise modern chemists:
Use "spShell" to graft quantum mechanical electron filling onto Lewis symbols:
Compare the electron dot filling methods:
FontSize (1)
Adjust the atomic symbol font size:
NetCharge (1)
Specify the charge for ions:
PairPlacement (1)
Specify the placement of paired electrons:
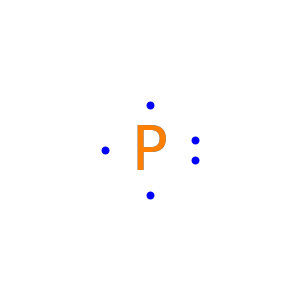
ValenceElectronCount (1)
Elements not contained in the s and p blocks of the periodic table may utilize electrons with different principle quantum numbers as valence electrons:
Applications (2)
Build Lewis structures for binary salts:
Typeset Lewis structures for binary salts:
Properties and Relations (3)
Lists are automatically threaded over:
PlotRange and ImageSize in combination with FontSize can be used to reduce the white space in a Lewis symbol:
Text results can be turned into Graphics:
Possible Issues (5)
Palladium fails since it has more than eight valence electrons:
Form the dication to see results:
A net charge larger than the number of valence electrons fails:
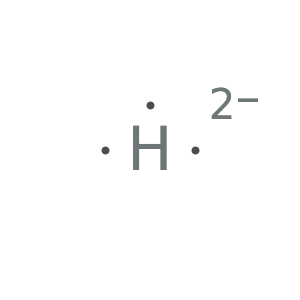
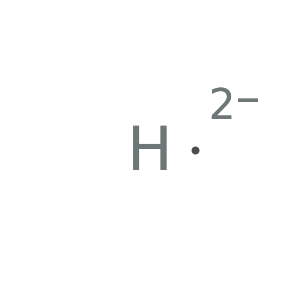
An anion with more than eight electrons fails:
The default valence electron count may be overly simplistic for elements not contained in the s and p blocks of the periodic table:
In this case two 7s electrons, three 5f electrons and one 6d electron are valence electrons:
Unexpected results may occur for ions that fill a shell:
Since Lewis symbols predate quantum mechanical electron configurations, use "ValenceElectronCount" to adjust the electron count:
Neat Examples (2)
Build the Lewis symbol for element 119:
Depict ionization reactions with Lewis electron-dot symbols:

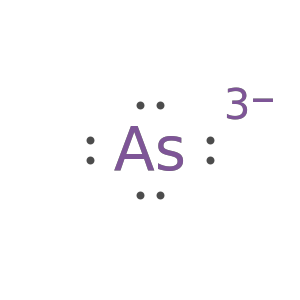






![GraphicsGrid[
Map[ResourceFunction["LewisSymbol"][
EntityValue[EntityClass["Element", "Period2"], "Entity"], Alignment -> #] &, {Center, Left, Right}],
Frame -> All, ImageSize -> 750
]](https://www.wolframcloud.com/obj/resourcesystem/images/2fb/2fbf28e4-75d4-4a61-bf14-7ff3c21b63c9/61abc73d0e1efb9c.png)
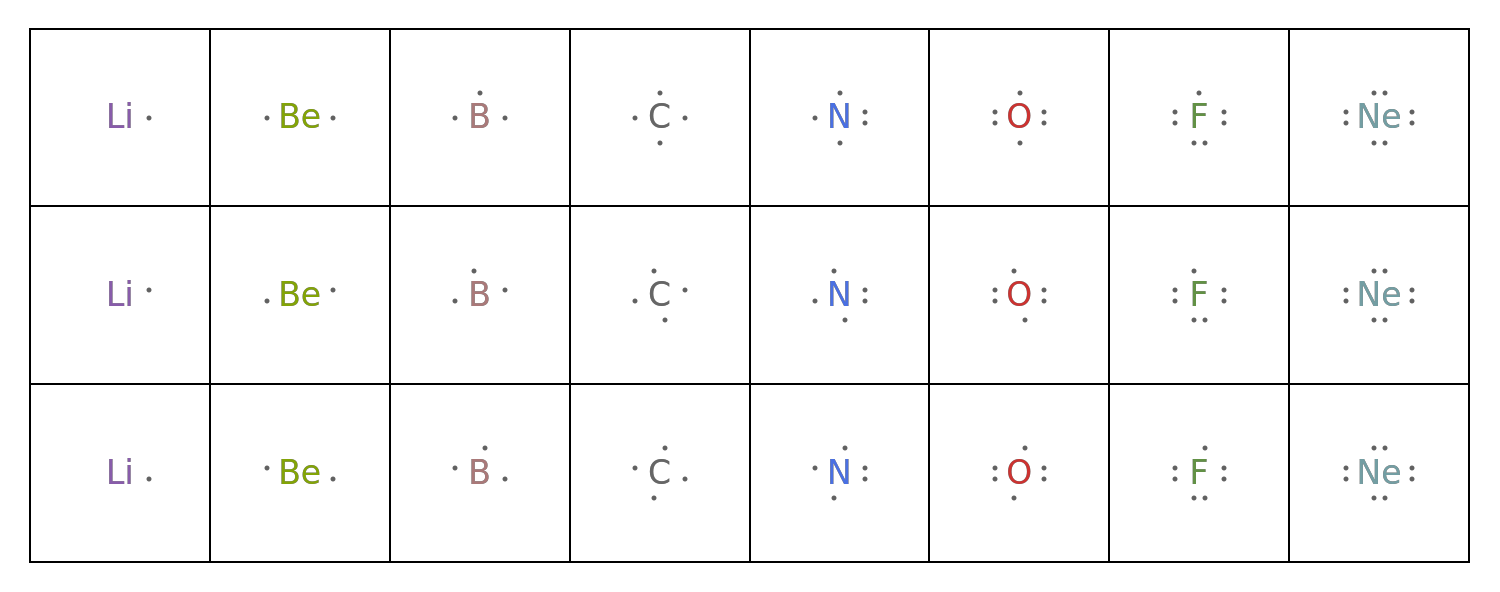



![GraphicsGrid[
Transpose[Map[
{#, ResourceFunction["LewisSymbol"][Entity["Element", "Cesium"], "DotPlacement" -> #]} &,
NestList[RotateLeft, {Right, Left, Above, Below}, 3]
]],
Frame -> All, ImageSize -> 750
]](https://www.wolframcloud.com/obj/resourcesystem/images/2fb/2fbf28e4-75d4-4a61-bf14-7ff3c21b63c9/66c669939944930b.png)

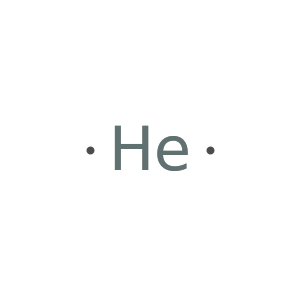
![GraphicsGrid[
Map[ResourceFunction["LewisSymbol"][
EntityValue[EntityClass["Element", "Period2"], "Entity"], "ElectronFilling" -> #] &, {"CubicalAtom", "spShell", "Unequal"}],
Frame -> All, ImageSize -> 750
]](https://www.wolframcloud.com/obj/resourcesystem/images/2fb/2fbf28e4-75d4-4a61-bf14-7ff3c21b63c9/7ef6c4cf1b2dc756.png)

![GraphicsGrid[
{Map[ResourceFunction["LewisSymbol"][Entity["Element", "Lithium"], "NetCharge" -> #] &, Range[1, -7, -1]],
Map[ResourceFunction["LewisSymbol"][Entity["Element", "Chlorine"], "NetCharge" -> #] &, Range[7, -1, -1]]},
Frame -> All, ImageSize -> 750
]](https://www.wolframcloud.com/obj/resourcesystem/images/2fb/2fbf28e4-75d4-4a61-bf14-7ff3c21b63c9/09efd798c6267538.png)
![GraphicsGrid[
Transpose[Map[
{#, ResourceFunction["LewisSymbol"][Entity["Element", "Antimony"], "PairPlacement" -> #]} &,
NestList[RotateLeft, {Right, Left, Above, Below}, 3]
]],
Frame -> All, ImageSize -> 750
]](https://www.wolframcloud.com/obj/resourcesystem/images/2fb/2fbf28e4-75d4-4a61-bf14-7ff3c21b63c9/31ed1bc448c046bc.png)
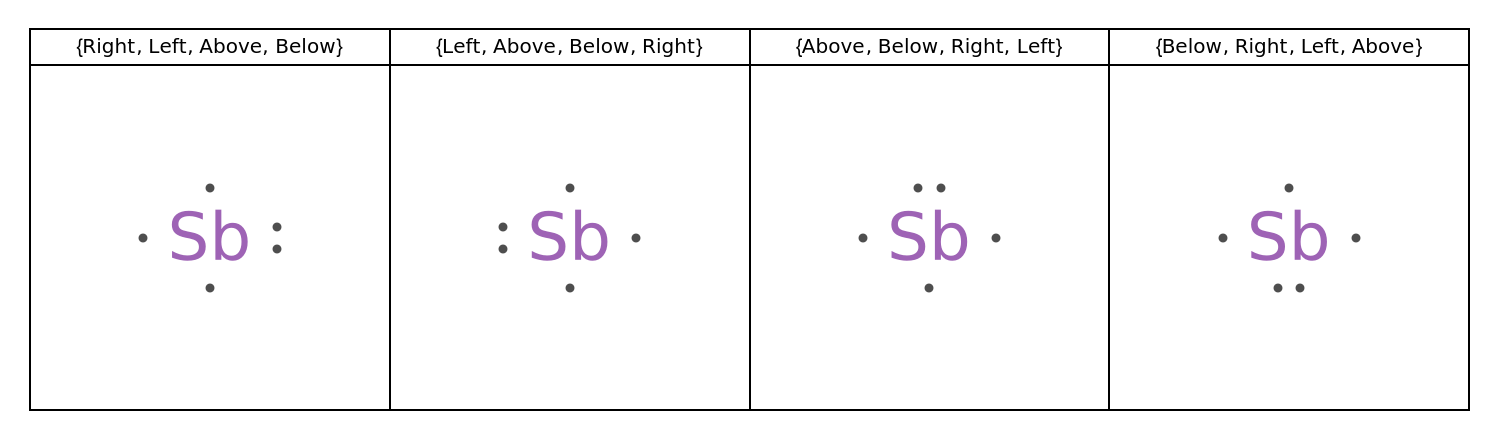

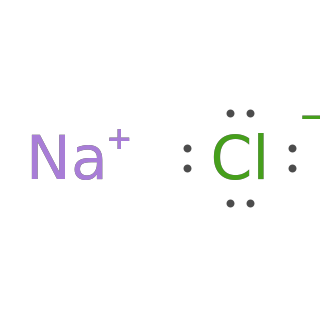


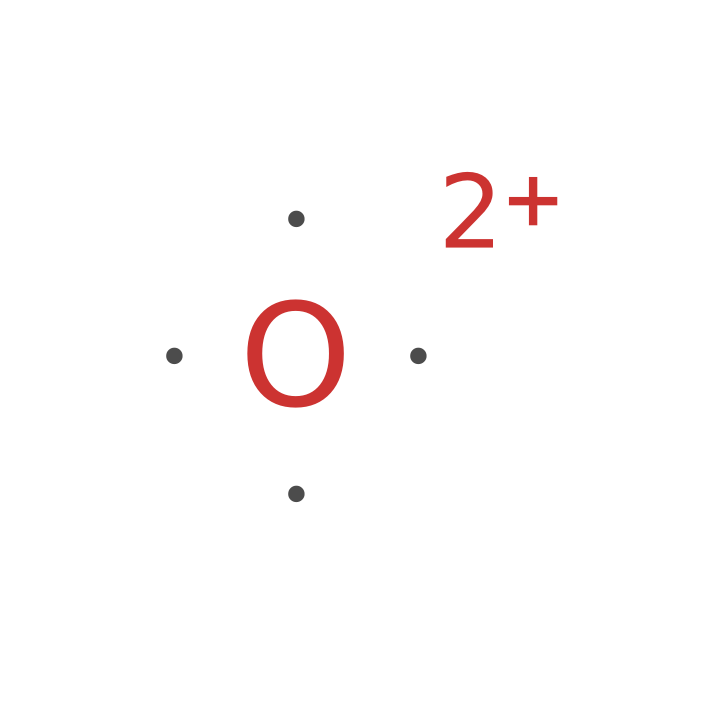
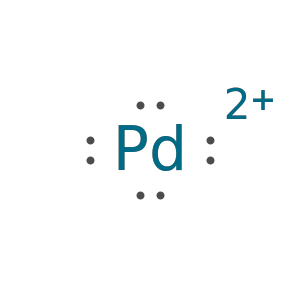


![Style[Row[{ResourceFunction["LewisSymbol"][
ChemicalFormula[{"Ca" -> 1}]], Row[{ResourceFunction["LewisSymbol"][
ChemicalFormula[{"Ca" -> 1}, <|"NetCharge" -> 2|>]], Row[{2, Entity["Particle", "Electron"][
EntityProperty["Particle", "FullSymbol"]]}]}, "+ "]}, "\[LongRightArrow]"],
FontSize -> Scaled[0.02]]](https://www.wolframcloud.com/obj/resourcesystem/images/2fb/2fbf28e4-75d4-4a61-bf14-7ff3c21b63c9/46fb893b92e84bf9.png)
