Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate interpolating nodes from points on a curve
ResourceFunction["LeeInterpolatingNodes"][{{x1,y1,…},{x2,y2,…},…}] yields centripetal interpolating nodes suitable for use with Interpolation from points assumed to be lying on a space curve. | |
ResourceFunction["LeeInterpolatingNodes"][{{x1,y1,…},{x2,y2,…},…},a] yields Lee's interpolating nodes with parameter a. |
| 0 | uniform parametrization |
| 1/2 | centripetal parametrization |
| 1 | chord length parametrization |
Generate centripetal interpolating nodes from a given set of points:
| In[1]:= |
| Out[1]= |
Use Interpolation to get an interpolating curve:
| In[2]:= |
| Out[2]= |
Plot the curve along with the original points:
| In[3]:= |
| Out[3]= | 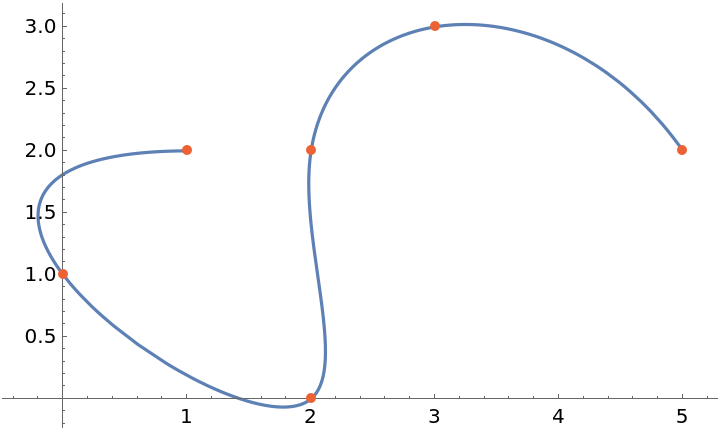 |
A set of 3D points:
| In[4]:= |
Generate an interpolating curve with uniform parametrization:
| In[5]:= | ![c1 = Interpolation[
Transpose[{ResourceFunction["LeeInterpolatingNodes"][pts, 0], pts}], Method -> "Spline"];
ParametricPlot3D[c1[t], {t, 0, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d74cd6-5f19-40e8-a46b-1779ed3058d3/41f87f16ee10bd0c.png) |
| Out[5]= | 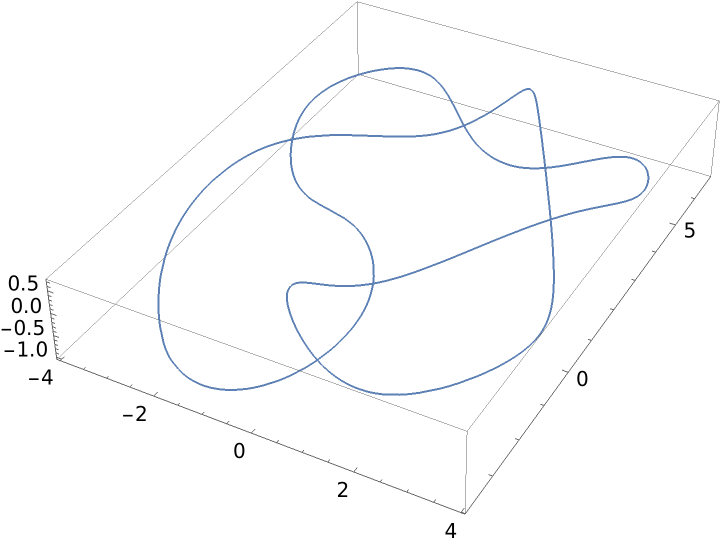 |
Generate an interpolating curve with chord length parametrization:
| In[6]:= | ![c1 = Interpolation[
Transpose[{ResourceFunction["LeeInterpolatingNodes"][pts, 1], pts}], Method -> "Spline"];
ParametricPlot3D[c1[t], {t, 0, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d74cd6-5f19-40e8-a46b-1779ed3058d3/2dd8b3821891f615.png) |
| Out[6]= | 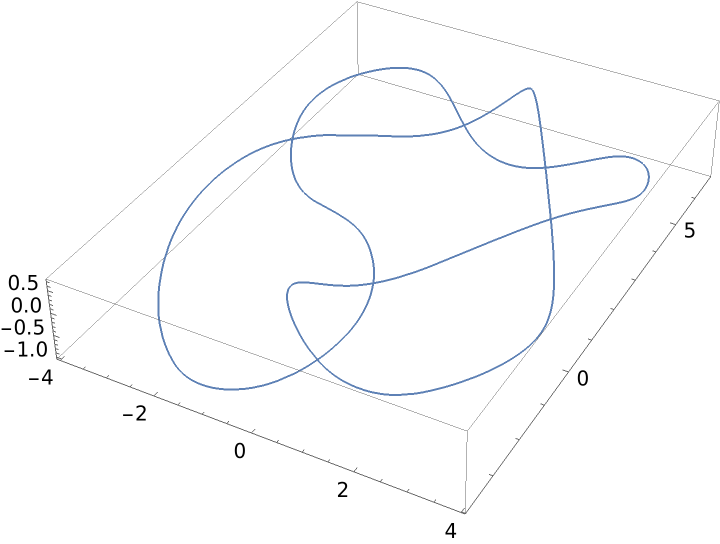 |
A set of 3D points:
| In[7]:= |
Generate the corresponding knots and control points for a B-spline curve:
| In[8]:= | ![With[{deg = 3, n = Length[cpts]},
tvals = ResourceFunction["LeeInterpolatingNodes"][cpts];
kp = Join[ConstantArray[0, deg + 1], MovingAverage[ArrayPad[tvals, -1], deg], ConstantArray[1, deg + 1]];
cp = LinearSolve[
Table[BSplineBasis[{deg, kp}, j - 1, tp], {tp, tvals}, {j, n}], cpts]] // Short](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d74cd6-5f19-40e8-a46b-1779ed3058d3/0c6baf9e3a118b23.png) |
| Out[8]= |
Visualize the B-spline curve and the points:
| In[9]:= | ![Graphics3D[{{Directive[ColorData[97, 1], AbsoluteThickness[2]], BSplineCurve[cp, SplineDegree -> 3, SplineKnots -> kp]}, {Directive[ColorData[97, 4], AbsolutePointSize[6]], Point[cpts]}}, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d74cd6-5f19-40e8-a46b-1779ed3058d3/3dd2ab83a6b06745.png) |
| Out[9]= | 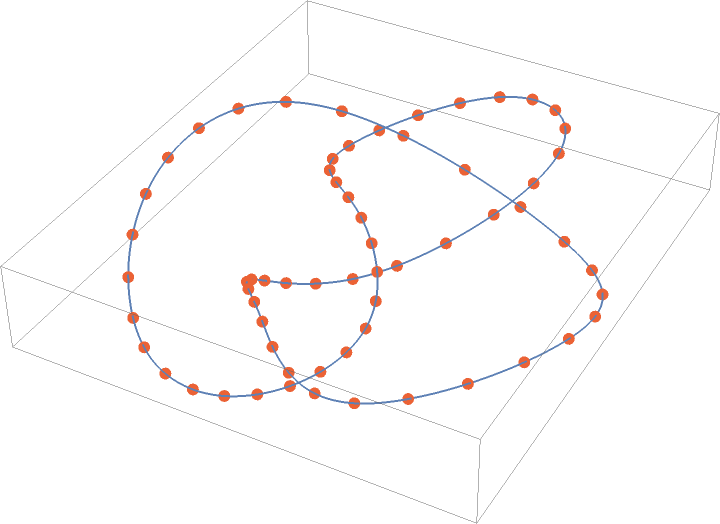 |
Demonstrate the effect of varying the parameter for the Lee interpolating nodes:
| In[10]:= | ![Manipulate[
With[{iF = Interpolation[
Transpose[{ResourceFunction["LeeInterpolatingNodes"][pex, a], pex}], Method -> "Spline"]},
ParametricPlot[iF[t], {t, 0, 1}, Epilog -> {Directive[AbsolutePointSize[5], ColorData[97, 4]], Point[pex]}, Sequence[
Frame -> True, PlotRange -> {{0, 31}, {0, 31}}, PlotRangePadding -> Scaled[0.05]]]], {{a, 1/2}, 0, 1}, Initialization :> (pex = {{0., 0.}, {1.34, 5.}, {5., 8.66}, {10., 10.}, {10.6, 10.4}, {10.7, 12.}, {10.7, 28.6}, {10.8, 30.2}, {
11.4, 30.6}, {19.6, 30.6}, {20.2, 30.2}, {20.3, 28.6}, {20.3, 12.}, {20.4, 10.4}, {21., 10.}, {26., 8.66}, {29.66, 5.}, {31., 0.}};), SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d74cd6-5f19-40e8-a46b-1779ed3058d3/0b9006f925e486c7.png) |
| Out[10]= | 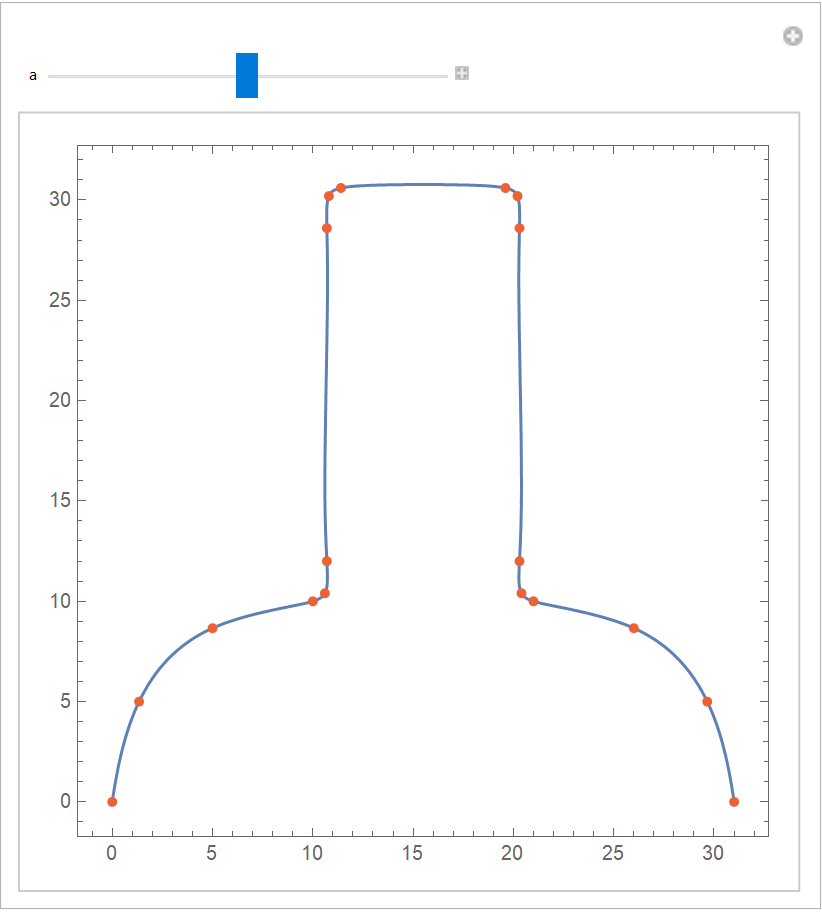 |
This work is licensed under a Creative Commons Attribution 4.0 International License