Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get lattice points in a variety of arrangements
ResourceFunction["LatticePointsArrangement"][arrangement,n] generates the first n lattice points based on arrangement. | |
ResourceFunction["LatticePointsArrangement"][] returns all the possible arrangements. |
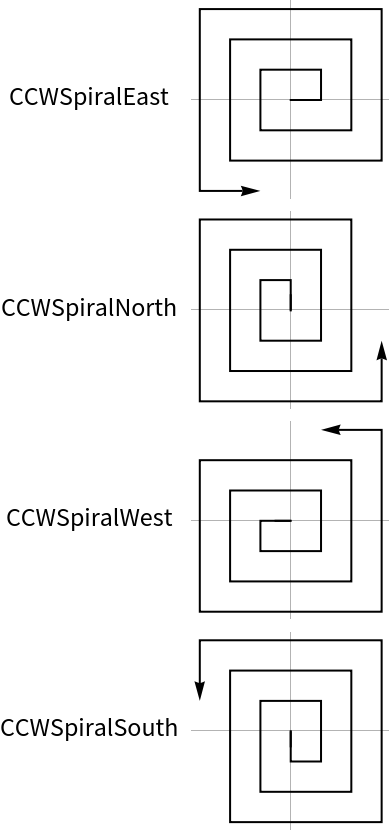

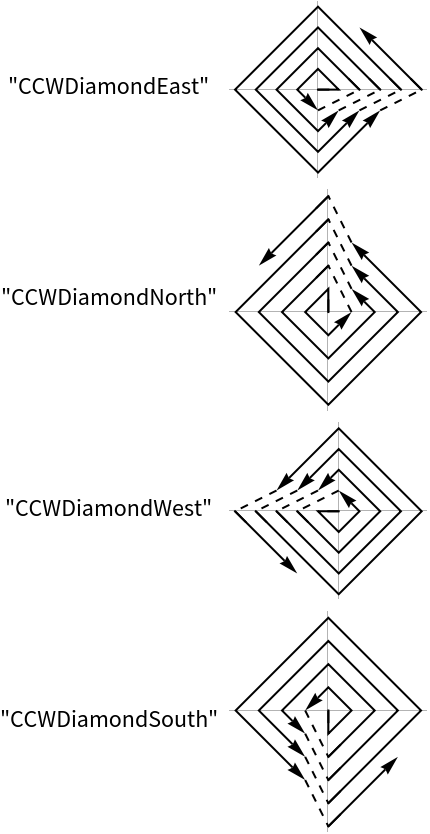
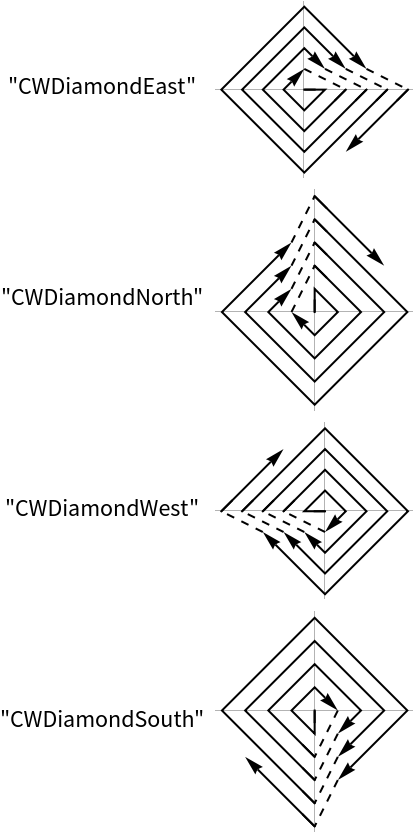
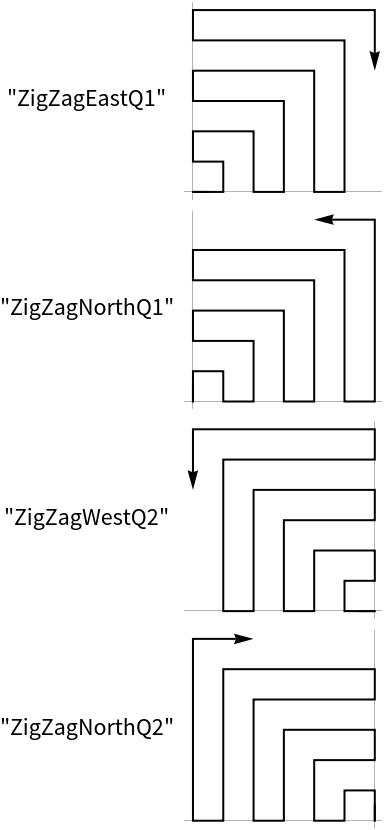
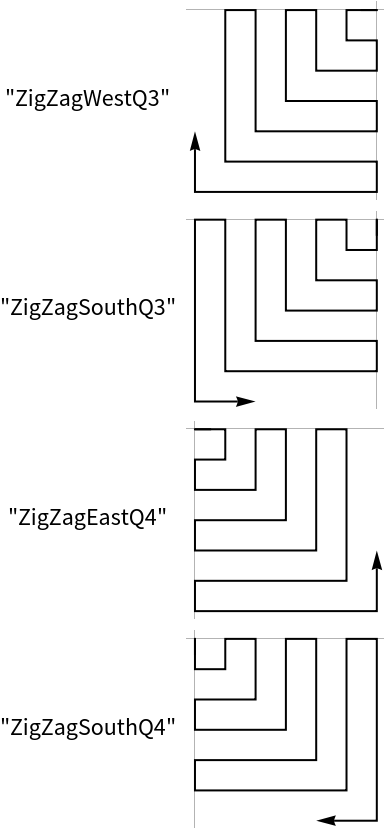
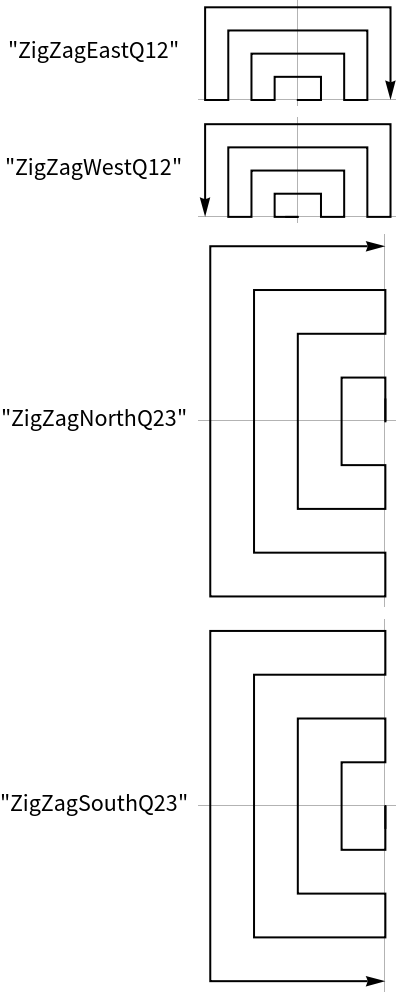

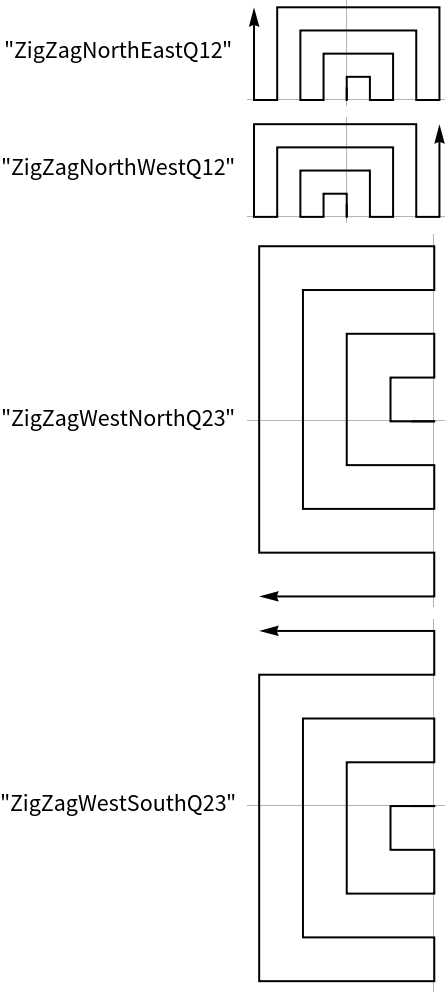
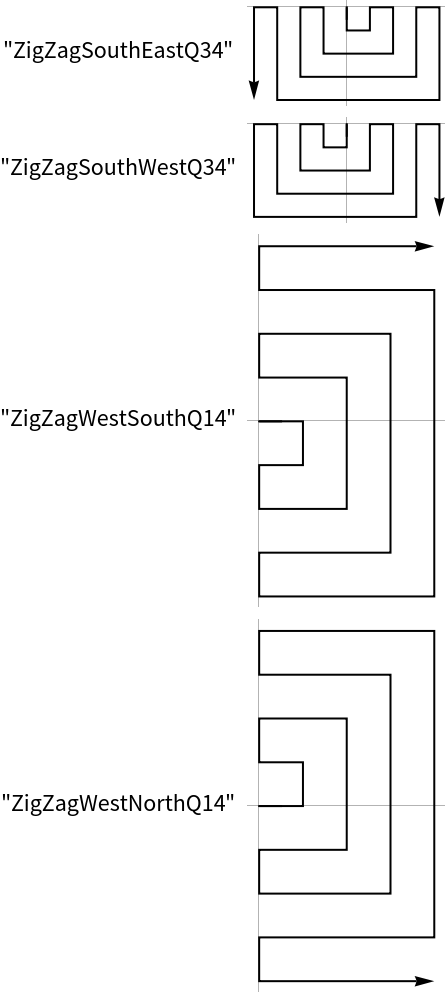
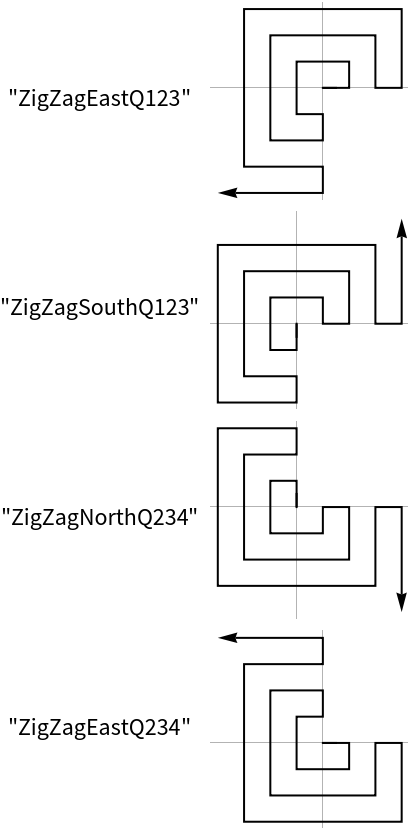

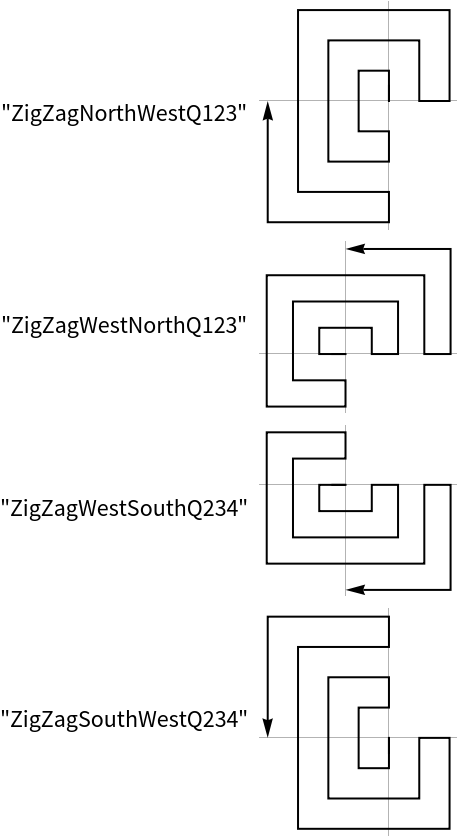
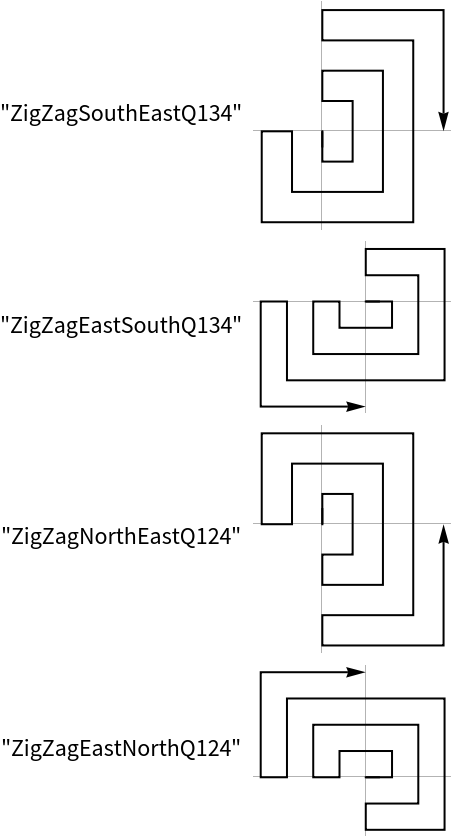


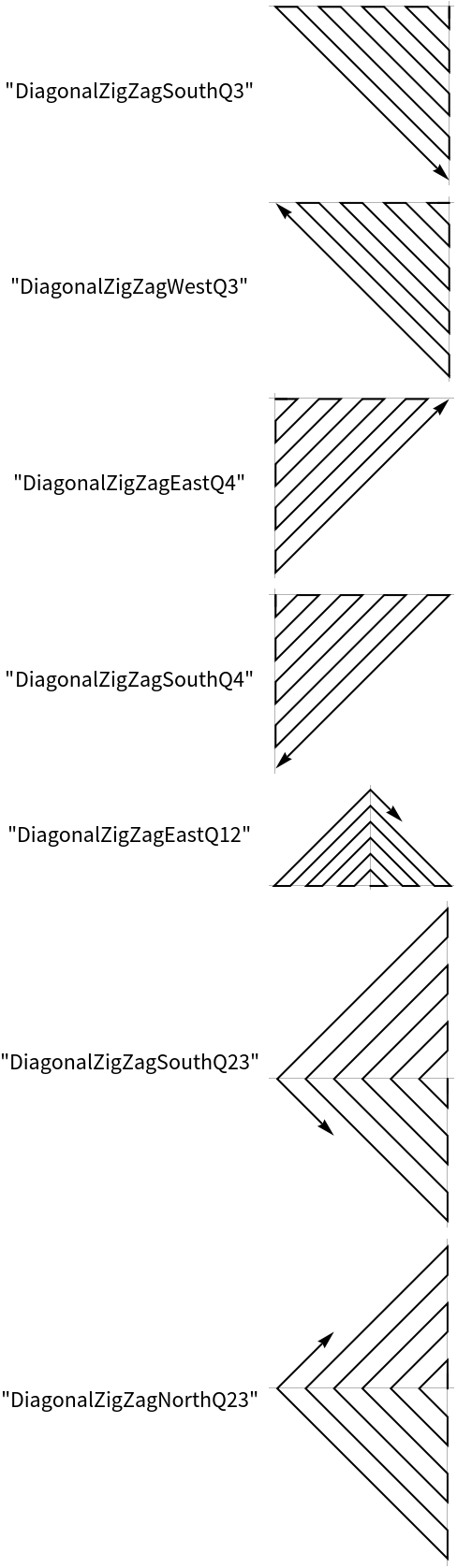

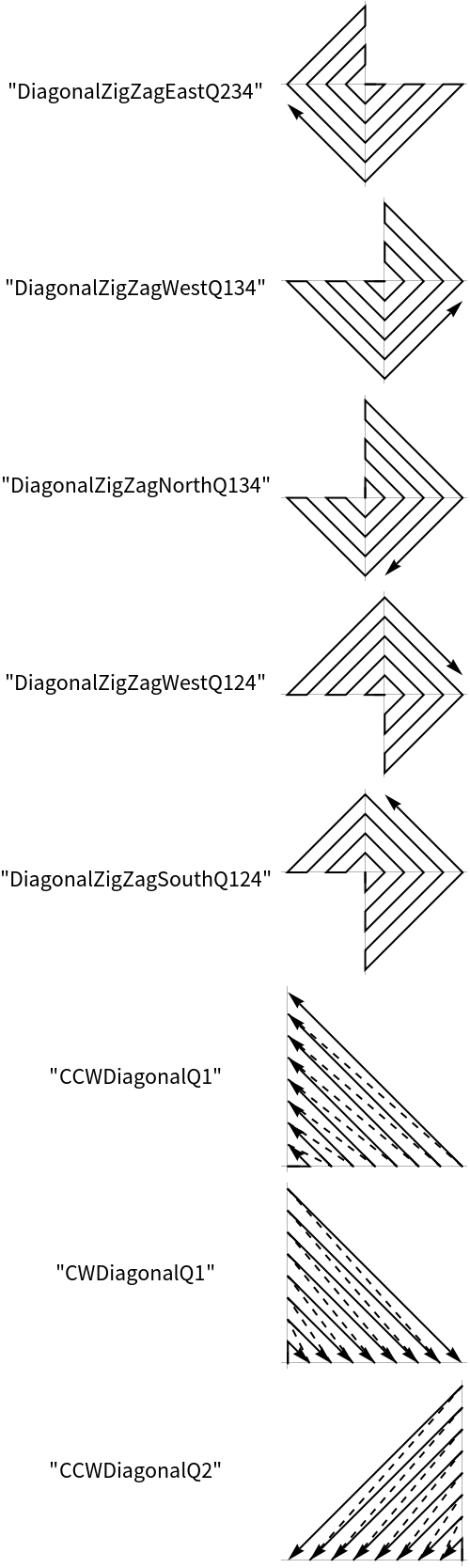
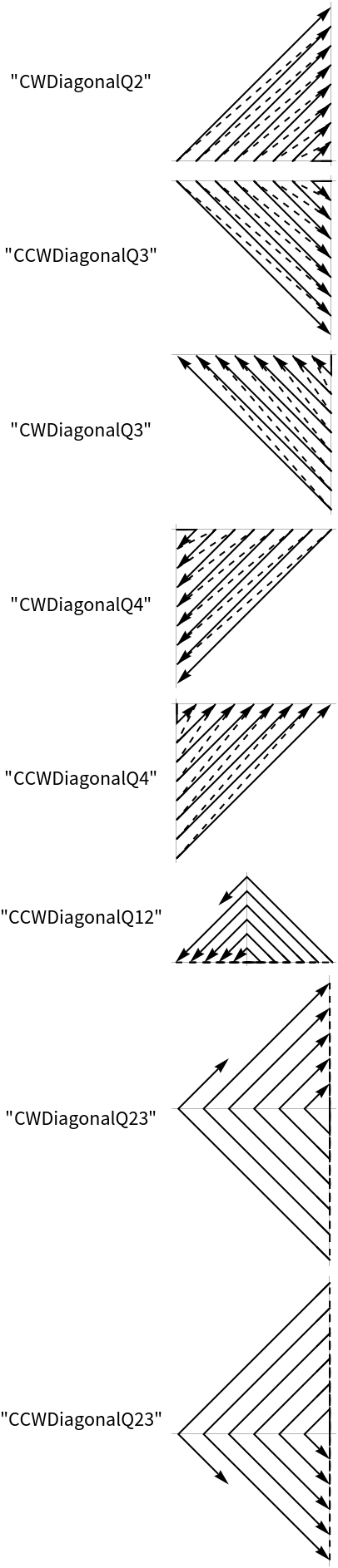



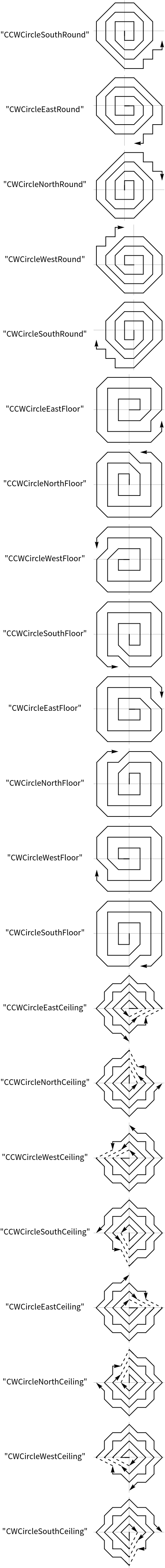
Create 20 points in a counter clock wise spiral starting in the eastern direction:
| In[1]:= |
| Out[1]= |
Create some points based on zigzagging diagonally in the first two quadrants:
| In[2]:= |
Visualize the points:
| In[3]:= |
| Out[3]= | 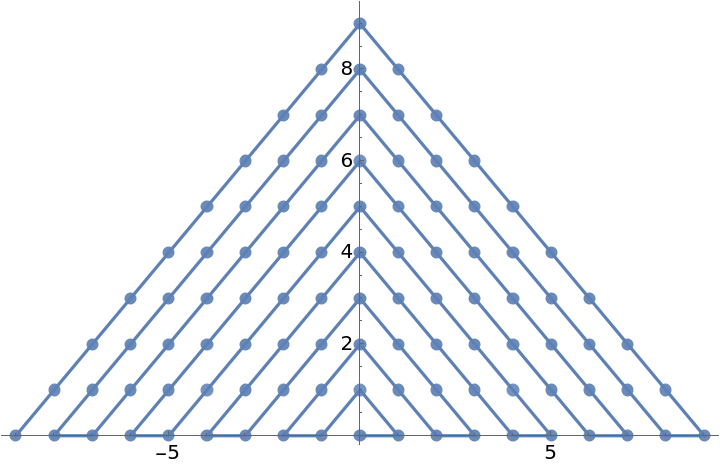 |
LatticePointsArrangement without any arguments returns all the possible arrangements:
| In[4]:= |
| Out[4]= |  |
Currently 160 arrangements are known:
| In[5]:= |
| Out[5]= |
Create the Ulam prime spiral:
| In[6]:= |
| Out[7]= |  |
Recreate the OEIS A316667 sequence of a horse moving on a spirally numbered board and moving to the lowest available unvisited square at each step:
| In[8]:= |
| In[9]:= | ![ShowRoute[output_Association] := Module[{colors},
colors = (ColorData["Rainbow"] /@ Subdivide[Length[output["Coordinates"]] - 1.0]);
Graphics[{Line[output["Coordinates"], VertexColors -> colors], Disk[Last@output["Coordinates"], 0.2]}]
];](https://www.wolframcloud.com/obj/resourcesystem/images/e42/e42fe59d-9cd4-4f48-a4e0-e23057debd8e/0d03ebe64a77c36a.png) |
| In[10]:= | ![MakeMove[spiral_Association, visited_List] := Module[{poss, hj},
poss = Table[Last[Last[visited]] + hj, {hj, horsejump}];
poss = DeleteMissing[{spiral[#], #} & /@ poss, 1, \[Infinity]];
poss = Select[poss, FreeQ[visited[[All, 2]], Last[#]] &];
If[Length[poss] > 0,
First[TakeSmallestBy[poss, First, 1]]
,
Missing[]
]
];](https://www.wolframcloud.com/obj/resourcesystem/images/e42/e42fe59d-9cd4-4f48-a4e0-e23057debd8e/75f5326dcb503d3d.png) |
| In[11]:= | ![FindSequence[start_ : {0, 0}, grid_] := Module[{positions, j, next},
positions = {{grid[start], start}};
PrintTemporary[Dynamic[j]];
Do[
next = MakeMove[grid, positions];
If[next =!= Missing[],
AppendTo[positions, next]
,
Break[];
]
,
{j, \[Infinity]}
];
<|"Coordinates" -> positions[[All, 2]], "Indices" -> positions[[All, 1]]|>
];](https://www.wolframcloud.com/obj/resourcesystem/images/e42/e42fe59d-9cd4-4f48-a4e0-e23057debd8e/12d8c38cbf37be33.png) |
| In[12]:= | ![grid = ResourceFunction["LatticePointsArrangement"]["CCWSpiralEast", 10000];
grid = Association[MapIndexed[#1 -> #2[[1]] &, grid]];
ShowRoute[FindSequence[{0, 0}, grid]]](https://www.wolframcloud.com/obj/resourcesystem/images/e42/e42fe59d-9cd4-4f48-a4e0-e23057debd8e/4f801688b11397f3.png) |
| Out[13]= | 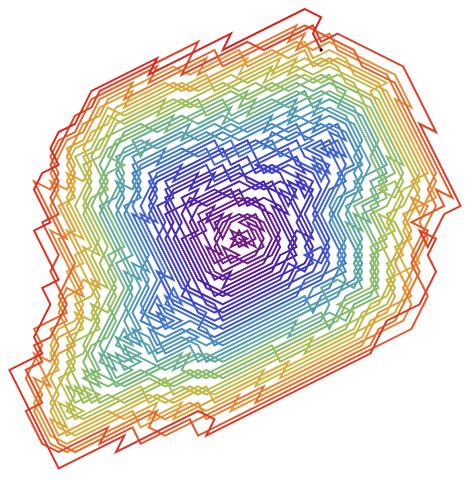 |
This work is licensed under a Creative Commons Attribution 4.0 International License