Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Lah number
ResourceFunction["LahL"][n,m] gives the Lah number L(n,m). |
Evaluate some Lah numbers:
| In[1]:= |
| Out[1]= |
LahL threads elementwise over lists:
| In[2]:= |
| Out[2]= |
Plot Lah numbers on a logarithmic scale:
| In[3]:= |
| Out[3]= | 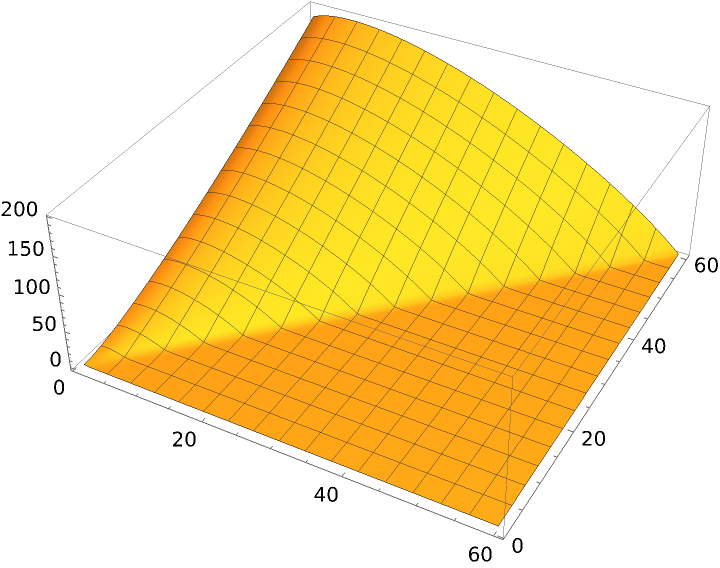 |
Express Pochhammer as a linear combination of FactorialPower:
| In[4]:= | ![With[{n = 7},
Pochhammer[x, n] == \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(m = 1\), \(n\)]\(\*
InterpretationBox[
TagBox[
FrameBox[
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.65 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["\<\"LahL\"\>", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->0.9 Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
Background->RGBColor[0.968627, 0.976471, 0.984314],
BaselinePosition->Baseline,
DefaultBaseStyle->{},
FrameMargins->{{0, 0}, {1, 1}},
FrameStyle->RGBColor[0.831373, 0.847059, 0.85098],
RoundingRadius->4],
{"FunctionResourceBox",
RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784],
"\"LahL\""},
TagBoxNote->"FunctionResourceBox"],
ResourceFunction["LahL"],
BoxID -> "LahL",
Selectable->False][n, m] FactorialPower[x, m]\)\)] // FunctionExpand // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/ecd/ecd725a2-f253-4a4e-ac0a-bc11c97887c4/6196dc3f52691263.png) |
| Out[4]= |
Express FactorialPower as a linear combination of Pochhammer:
| In[5]:= | ![With[{n = 7},
FactorialPower[x, n] == \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(m = 1\), \(n\)]\(
\*SuperscriptBox[\((\(-1\))\), \(n - m\)] \*
InterpretationBox[
TagBox[
FrameBox[
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.65 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["\<\"LahL\"\>", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->0.9 Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
Background->RGBColor[0.968627, 0.976471, 0.984314],
BaselinePosition->Baseline,
DefaultBaseStyle->{},
FrameMargins->{{0, 0}, {1, 1}},
FrameStyle->RGBColor[0.831373, 0.847059, 0.85098],
RoundingRadius->4],
{"FunctionResourceBox",
RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784],
"\"LahL\""},
TagBoxNote->"FunctionResourceBox"],
ResourceFunction["LahL"],
BoxID -> "LahL",
Selectable->False][n, m] Pochhammer[x, m]\)\)] // FunctionExpand // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/ecd/ecd725a2-f253-4a4e-ac0a-bc11c97887c4/7e5a4e9a6a1b6e44.png) |
| Out[5]= |
Closed form of derivatives of ⅇ1/x:
| In[6]:= |
| Out[6]= |
| In[7]:= | ![With[{n = 6}, (-1)^n Exp[1/x] \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(n\)]\*
FractionBox[
RowBox[{
InterpretationBox[
TagBox[
FrameBox[
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.65 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["\<\"LahL\"\>", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->0.9 Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
Background->RGBColor[0.968627, 0.976471, 0.984314],
BaselinePosition->Baseline,
DefaultBaseStyle->{},
FrameMargins->{{0, 0}, {1, 1}},
FrameStyle->RGBColor[0.831373, 0.847059, 0.85098],
RoundingRadius->4],
{"FunctionResourceBox",
RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784],
"\"LahL\""},
TagBoxNote->"FunctionResourceBox"],
ResourceFunction["LahL"],
BoxID -> "LahL",
Selectable->False], "[",
RowBox[{"n", ",", "k"}], "]"}],
SuperscriptBox["x",
RowBox[{"n", "+", "k"}]]]\)] // Factor](https://www.wolframcloud.com/obj/resourcesystem/images/ecd/ecd725a2-f253-4a4e-ac0a-bc11c97887c4/48bf0c6a887c2ad8.png) |
| Out[7]= |
Generate values from the generating function:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
Lah numbers can be expressed in terms of Stirling numbers of both kinds:
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
Lah numbers are given by a partial Bell polynomial with factorial arguments:
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
This work is licensed under a Creative Commons Attribution 4.0 International License