Basic Examples (6)
Compute data about the gravitational potential:
Find the gravitational potential at a specific 3D point:
Create a contour plot of the gravitational potential:
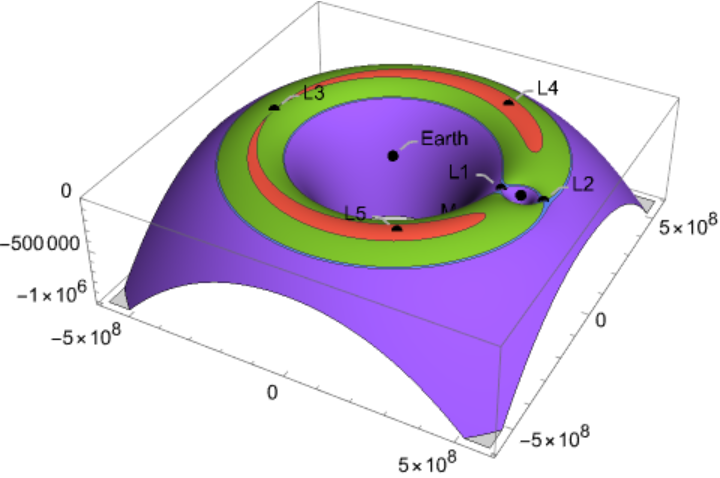
Create a 3D surface plot of the gravitational potential:
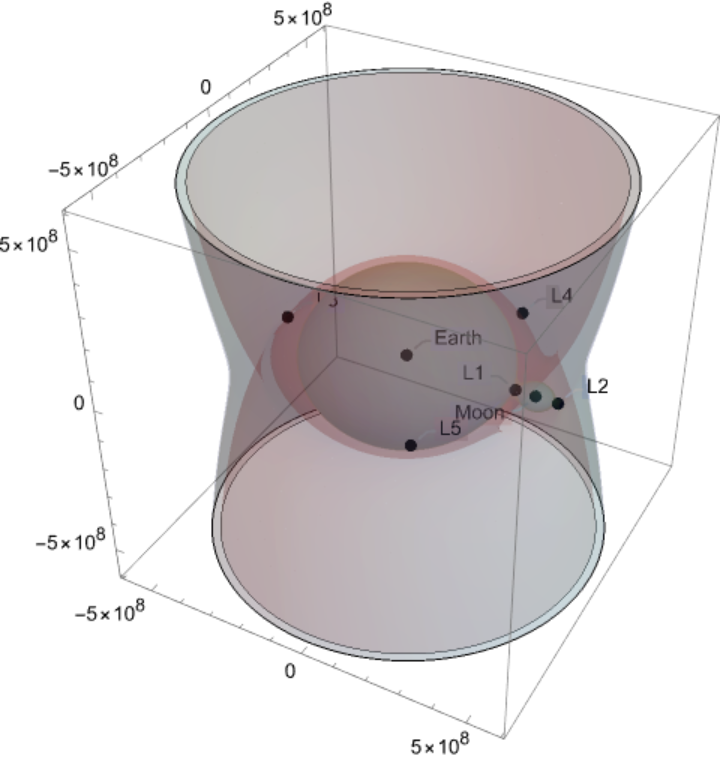
Create a 3D contour plot of the gravitational potential:
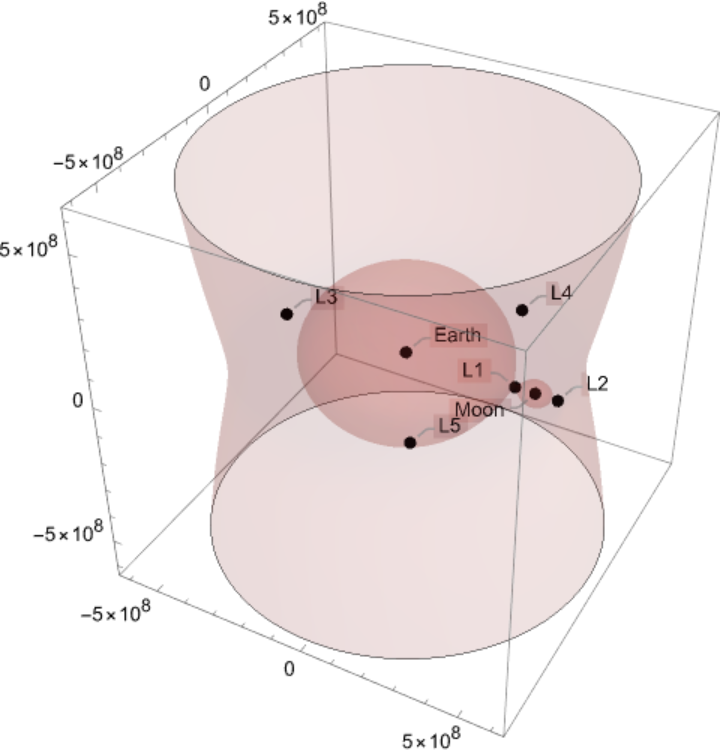
Compute the current distance between both bodies and the various Lagrange points:
Compute the distance between both bodies and the various Lagrange points on a specified date:
Scope (1)
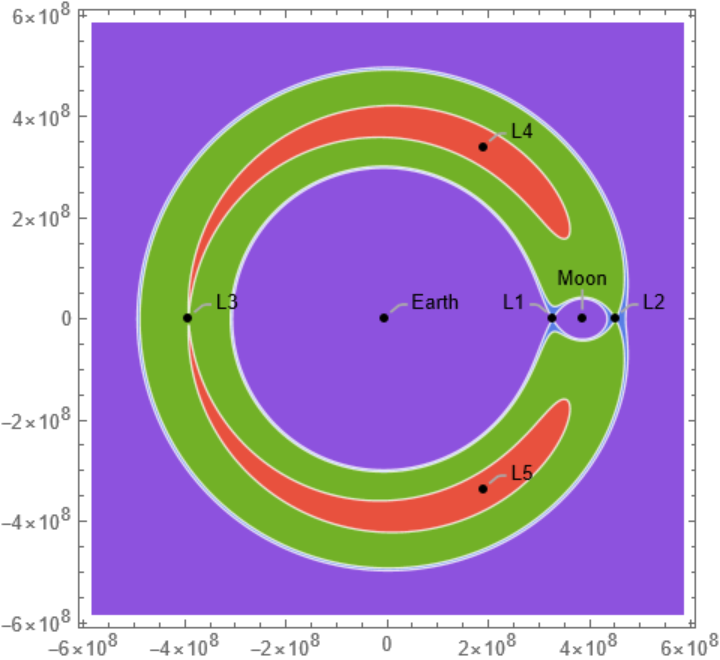
Create a contour plot with distances:
Options (3)
Emphasize the area around the secondary mass:
Emphasize the area around the secondary mass:
Emphasize the area around the secondary mass:
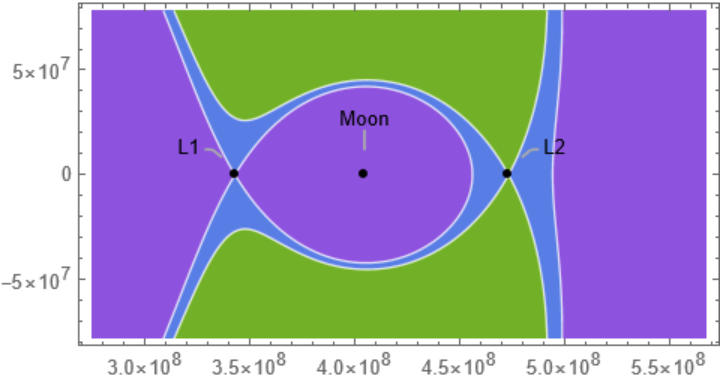
Plot the Lagrange points:
Applications (4)
Compute the distances of the bodies to the L1 point of the Earth-Moon system:
Compute the distance of the Earth to the L1 point of the Earth-Moon system:
Compute the distance between the Moon and the L1 point of the Earth-Moon system:
Compute the distance between Earth and the Moon:
Possible Issues (1)
If the two bodies don't orbit each other, then computations are not applicable:
Neat Examples (3)
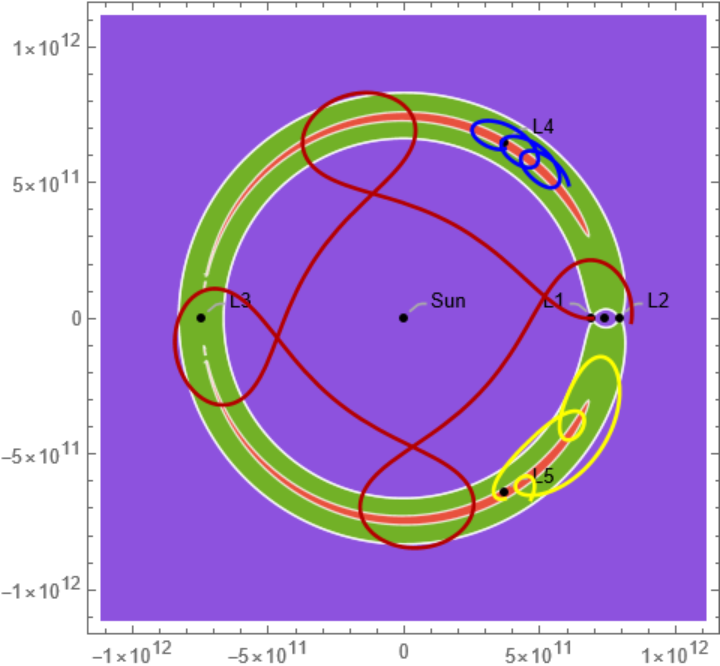
Explore the Lagrange points of the Sun‐Jupiter system:
Solve the equations of motion for a particle starting at the L1 point and moving in the -x‐direction and -y‐direction over a period of about 31 years (1,000,000,000 seconds):
Solve the equations of motion for particle starting near the L4 and L5 points with different initial velocities:
![ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}, "GravitationalEffectivePotentialData"]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/2d377b0c93428e1c.png)

![ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}, "GravitationalEffectivePotentialData"]["Potential"][
Quantity[3.44*^8, "Meters"], Quantity[0, "Meters"], Quantity[0, "Meters"]]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/78381229c52514eb.png)
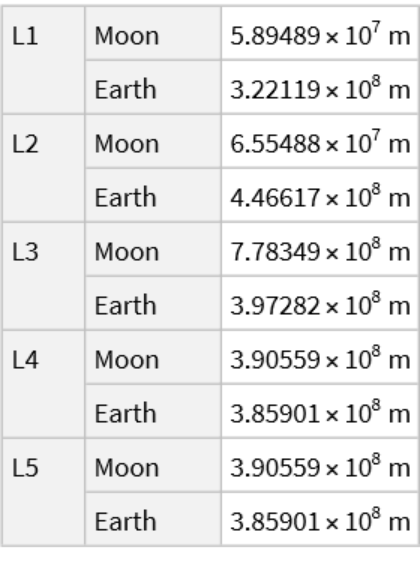
![ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}, DateObject[{2024, 7, 16, 0, 0, 0}, TimeZone -> "America/Chicago"], "Distances"]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/082639ca4913aed2.png)
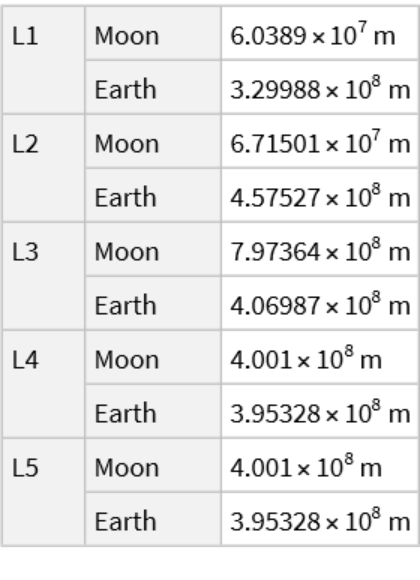
![Grid[{ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["MinorPlanet", "Pluto"], Entity["PlanetaryMoon", "Charon"]}, {"ContourPlot", "Distances"}, ImageSize -> 300, TargetUnits -> "Kilometers"]}]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/0cc8b7bd15229529.png)
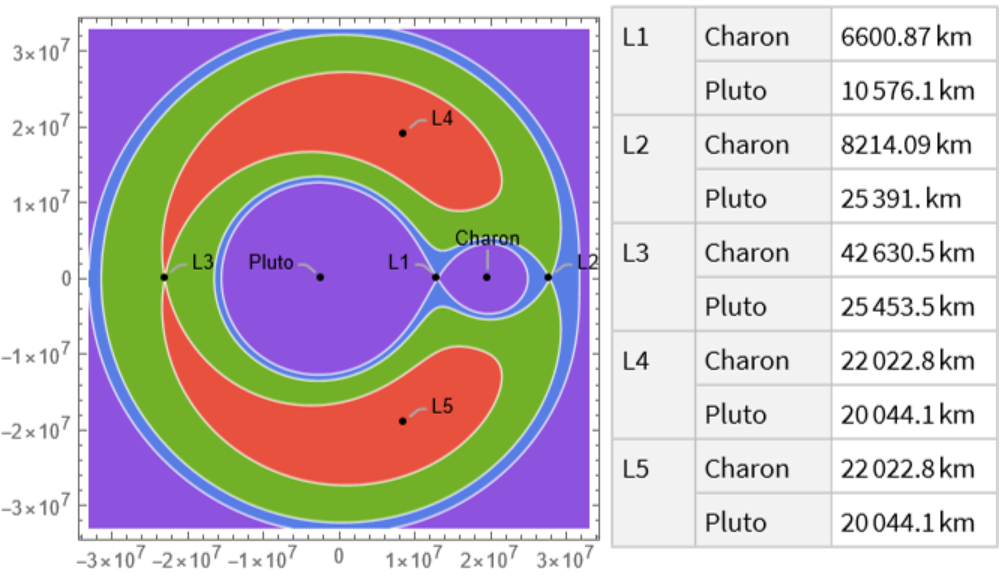
![ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}, "ContourPlot", "EmphasizeSecondaryMassRegion" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/259dc68311bcac63.png)
![ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}, "Plot3D", "EmphasizeSecondaryMassRegion" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/7715d71ad6da4dee.png)
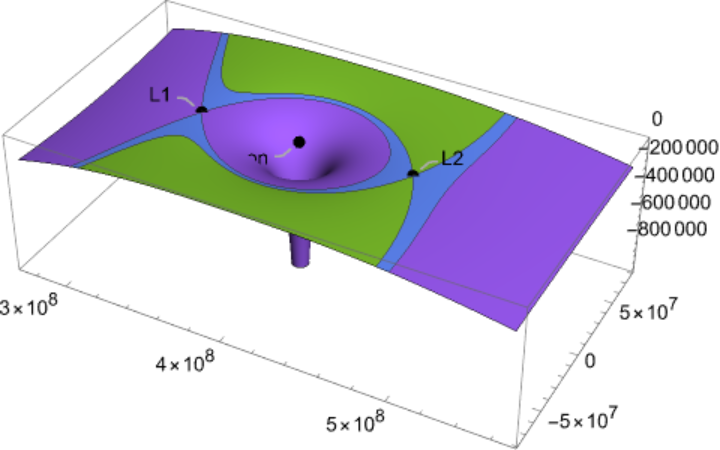
![ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}, "ContourPlot3D", "EmphasizeSecondaryMassRegion" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/62a6d2b5d787865d.png)
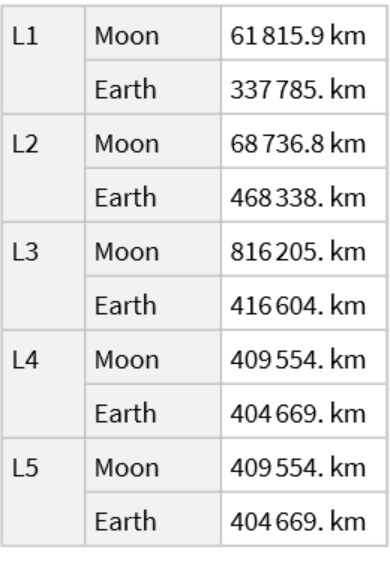
![ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}, "Distances", TargetUnits -> "Kilometers"]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/229e3bb9e8bacd00.png)
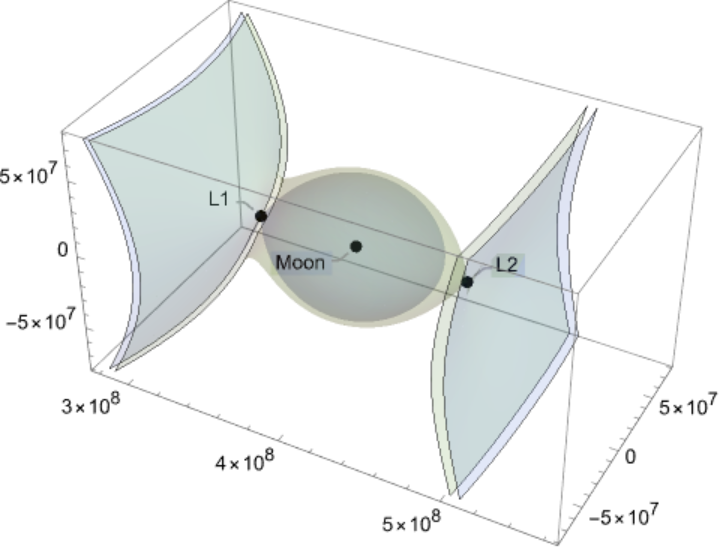
![With[{entities = {Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}}, ResourceFunction["LagrangePointData"][entities, "ContourPlot3D", Contours -> {QuantityMagnitude[
ResourceFunction["LagrangePointData"][entities, "GravitationalEffectivePotentialData"]["L1Potential"]]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/76d8bc54cd3003e7.png)
![ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}, "Distances", TargetUnits -> "Kilometers"]["L1"]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/69029eeada92168f.png)
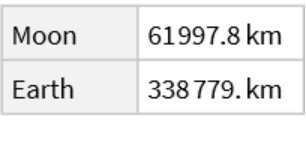
![ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}, "Distances", TargetUnits -> "Kilometers"]["L1"][Entity["Planet", "Earth"]]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/150b2078609b92e7.png)
![ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Planet", "Earth"], Entity["PlanetaryMoon", "Moon"]}, "Distances", TargetUnits -> "Kilometers"]["L1"][Entity["PlanetaryMoon", "Moon"]]](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/748dde8e50b040cf.png)
![{\[Omega], V, L1, L4, L5, cp} = Flatten[{{QuantityMagnitude[#[[1]]], #[[2]][x[t], y[t], z[t]], QuantityMagnitude[#[[3]]], QuantityMagnitude[#[[4]]], QuantityMagnitude[#[[5]]]} &@
Lookup[#[[1]], {"\[Omega]", "NondimensionalizedPotential", "L1Position", "L4Position", "L5Position"}], #[[2]]} &@
ResourceFunction["LagrangePointData", ResourceVersion->"1.0.0"][{Entity["Star", "Sun"], Entity["Planet", "Jupiter"]}, {"GravitationalEffectivePotentialData", "ContourPlot"}], 1] /. z[t] -> 0;](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/552acdd617a11d95.png)
![L1sols = NDSolve[{x''[t] - 2 \[Omega] y'[t] == -D[V, x[t]], y''[t] + 2 \[Omega] x'[t] == -D[V, y[t]], x'[0] == -5000., y'[0] == -300., x[0] == L1[[1]], y[0] == L1[[2]], z[0] == L1[[3]]}, {x, y}, {t, 0, 1000000000}];](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/1cde95576e951b30.png)
![L4sols = NDSolve[{x''[t] - 2 \[Omega] y'[t] == -D[V, x[t]], y''[t] + 2 \[Omega] x'[t] == -D[V, y[t]], x'[0] == -1000., y'[0] == -300., x[0] == L4[[1]], y[0] == L4[[2]] - 20000000000, z[0] == L4[[3]]}, {x, y}, {t, 0, 1000000000}];](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/78bb012c360b07e4.png)
![L5sols = NDSolve[{x''[t] - 2 \[Omega] y'[t] == -D[V, x[t]], y''[t] + 2 \[Omega] x'[t] == -D[V, y[t]], x'[0] == -1000., y'[0] == -300., x[0] == L5[[1]], y[0] == L5[[2]] - 20000000000, z[0] == L5[[3]]}, {x, y}, {t, 0, 1000000000}];](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/1a9d39b587bfe7a2.png)
![L1path = ParametricPlot[Evaluate[{x[t], y[t]} /. L1sols], {t, 0, 1000000000},
PlotStyle -> Darker[Red, .3]];](https://www.wolframcloud.com/obj/resourcesystem/images/5b5/5b5e56d3-2ec1-4f5b-a09d-9dd802a61a86/1-0-0/0b18320d08358bc1.png)