Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 LSystemPlot

Source Notebook

Display an L-system

Contributed by: Robert Dickau

ResourceFunction["LSystemPlot"][rules,axiom,n,delta]

displays the L-string for the nth iteration of the list rules, starting with the string axiom after n iterations with an angle delta.

Details and Options

An L-system or Lindenmayer system is a parallel rewriting system that consists of a set of characters to produce strings and a list of production rules that replace each symbol from an initial "axiom" string a number of times. The L-system also needs a way to give the string a graphical meaning.
"F" is an instruction to draw a line segment one unit in the current direction. A plus sign (+) is an instruction to rotate the current direction one angular unit clockwise, and a minus sign (-) is an instruction to rotate the current direction one angular unit counterclockwise.
String replacements are made in parallel.

Examples

Basic Examples (4) 

Four steps for Koch quadratic rules:

In[1]:=
ResourceFunction["LSystemPlot"][{"F" -> "FF-F-F-F-F-F+F"}, "F-F-F-F", 4]
Out[1]=

Get just the resulting string after only one step:

In[2]:=
Last[SubstitutionSystem[{"F" -> "FF-F-F-F-F-F+F"}, "F-F-F-F", 1]]
Out[2]=

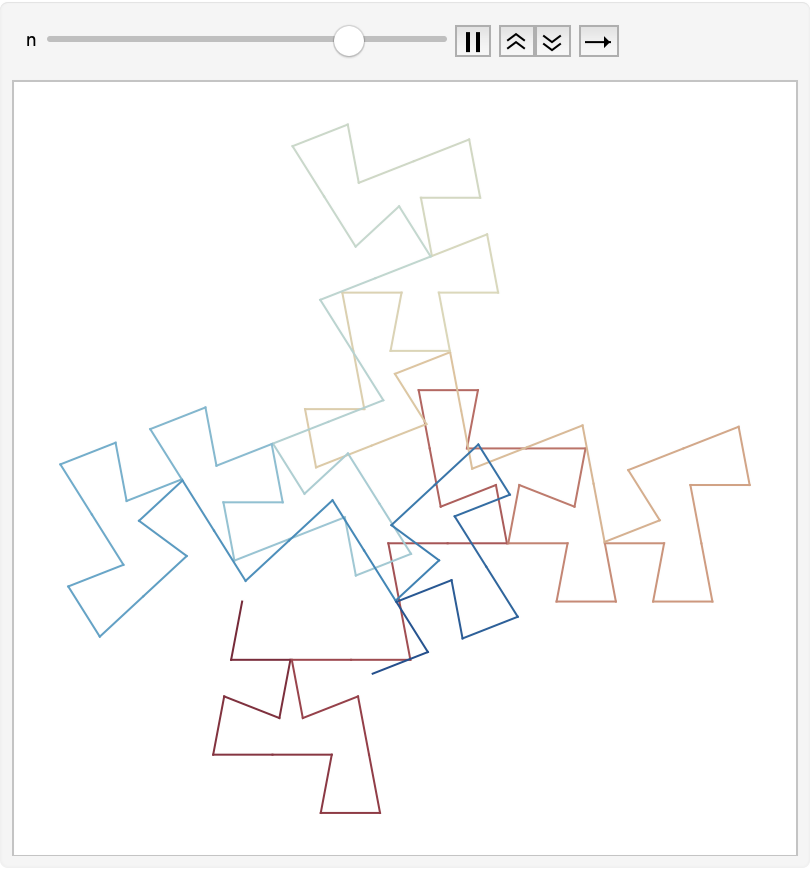
Continuously modify the angle:

In[3]:=
Animate[ResourceFunction[ "LSystemPlot"][{"F" -> "-F+F-F-F+F+FF-F+F+FF+F-F-FF+FF-FF+F+F-FF-F-F+FF-F-F+F+F-F+"}, "F+F+F+F", 1, n Degree, ColorFunction -> ColorData["RedBlueTones"]], {n, 30., 120.}]
Out[3]=

Grid for named fractals:

In[4]:=
lsystems = {{"32\[Hyphen]segment curve", {"F" -> "-F+F-F-F+F+FF-F+F+FF+F-F-FF+FF-FF+F+F-FF-F-F+FF-F-F+F+F-F+"}, "F+F+F+F", 2, 90}, {"box fractal", {"F" -> "F-F+F+F-F"}, "F-F-F-F", 3, 90}, {"dragon curve", {"X" -> "X+YF+", "Y" -> "-FX-Y"}, "FX", 10, 90}, {"Hilbert curve", {"L" -> "+RF-LFL-FR+", "R" -> "-LF+RFR+FL-"}, "L", 4, 90}, {"Hilbert curve II", {"X" -> "XFYFX+F+YFXFY-F-XFYFX", "Y" -> "YFXFY-F-XFYFX+F+YFXFY"}, "X", 3, 90}, {"Koch snowflake", {"F" -> "F+F--F+F"}, "F--F--F", 3, 60}, {"Peano curve", {"F" -> "F+F-F-F-F+F+F+F-F"}, "F", 2, 90}, {"Peano\[Hyphen]Gosper curve", {"X" -> "X+YF++YF-FX--FXFX-YF+", "Y" -> "-FX+YFYF++YF+FX--FX-Y"}, "FX", 3, 60}, {"quadratic Koch island", {"F" -> "F-F+F+FFF-F-F+F"}, "F+F+F+F", 2, 90}, {"Sierpiński arrowhead", {"X" -> "YF+XF+Y", "Y" -> "XF-YF-X"}, "YF", 5, 60}, {"Sierpiński curve", {"X" -> "XF-F+F-XF+F+XF-F+F-X"}, "F+XF+F+XF", 3, 90}, {"Siepiński sieve", {"F" -> "FF", "X" -> "--FXF++FXF++FXF--"}, "FXF--FF--FF", 4, 60}};
In[5]:=
GraphicsGrid[ Partition[ ResourceFunction["LSystemPlot"][Sequence @@ (Take[#, {2, -2}]), Last[#] Degree // N, PlotLabel -> First[#], BaseStyle -> {FontFamily -> "Times", FontSlant -> "Italic"}] & /@ lsystems, 4], ImageSize -> 600]
Out[5]=

Options (2) 

ColorData (1) 

Select a gradient color function:

In[6]:=
ResourceFunction["LSystemPlot"][{"F" -> "FF-F+F-F-FF"}, "F-F-F-F", 4, ColorFunction -> ColorData["RedBlueTones"]]
Out[6]=

PlotStyle (1) 

Add Graphics options:

In[7]:=
ResourceFunction["LSystemPlot"][{"F" -> "F+F--F+F"}, "F", 3, \[Pi]/3, ColorFunction -> ColorData["RedBlueTones"], PlotStyle -> Dashed, Background -> Black]
Out[7]=

Applications (3) 

Convert to a BSplineCurve:

In[8]:=
sc32 = ResourceFunction[ "LSystemPlot"][{"F" -> "-F+F-F-F+F+FF-F+F+FF+F-F-FF+FF-FF+F+F-FF-F-F+FF-F-F+F+F-F+"}, "F+F+F+F", 1];
In[9]:=
Graphics[{Red, FilledCurve[ BSplineCurve[Cases[sc32, Line[{a_, b_}] -> a, \[Infinity]], SplineClosed -> True]]}]
Out[9]=
In[10]:=
With[{sp = FilledCurve[ BSplineCurve[Cases[sc32, Line[{a_, b_}] -> a, \[Infinity]], SplineClosed -> True]]}, Graphics[{Opacity[.5], Red, sp, Blue, Rotate[sp, \[Pi]/3], Yellow, Rotate[sp, 2 \[Pi]/3]}]]
Out[10]=

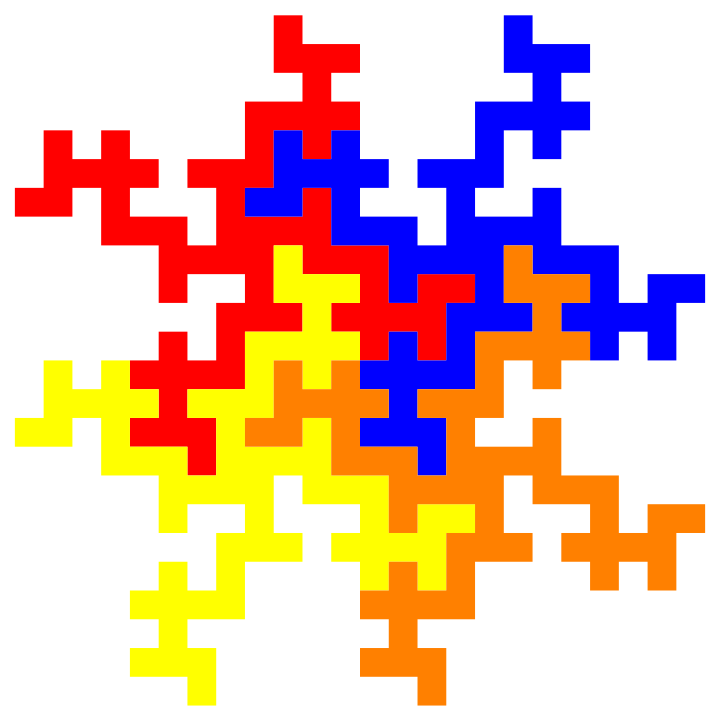
Make a tessellation:

In[11]:=
With[{fc = Polygon[Cases[sc32, Line[{a_, b_}] -> a, \[Infinity]]]}, Graphics[{Red, fc, Blue, Translate[fc, {8, 0}], Yellow, Translate[fc, {0, -8}], Orange, Translate[fc, {8, -8}]}]]
Out[11]=

Go to 3D:

In[12]:=
coords = With[{pts = Cases[sc32, Line[{a_, b_}] -> a, \[Infinity]]}, {(Polygon[{Append[#1[[1]], 0.], Append[#1[[2]], 0.], Append[#1[[2]], 3.], Append[#1[[1]], 3.]}] &) /@ Partition[pts, 2, 1], Polygon[Append[#1, 3.] & /@ pts]}];
In[13]:=
Graphics3D[{Red, coords}, Boxed -> False]
Out[13]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 01 April 2019

Related Resources

License Information