Function Repository Resource:

LSystem

Generate an L-system

Contributed by: Renan Soares Germano

ResourceFunction["LSystem"][rules,init,t,θ]

returns an Association containing the word and the branches generated after executing the L-system represented by rules from initial word init for t steps, with movement specified by the angle θ.

Details and Options

L-system is also known as a Lindenmayer system.

θ is taken to be in degrees.

The following special symbols, when present in rules, represent the following instructions:

increase the current angle by θ

decrease the current angle by θ

[

start a new branch

]

close the current branch

ResourceFunction["LSystem"] takes the following options:

"InitialAngle"

initial angle in degrees from which the next points will be generated

"InitialPoint"

{0,0}

intial point from which the next points will be generated

"MoveLength"

distance of a new point from the previous one

Any other symbol will be interpreted as an instruction to move forward.

In an L-system with brackets, every left bracket "[" must be paired with a right bracket "]" in the rules and the initial word.

Examples

Basic Examples (4)

Run a simple L-system for one iteration:

In[1]:=

Out[1]=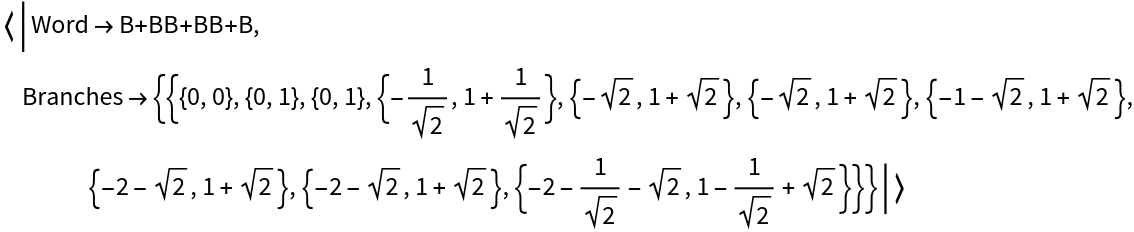

Because this L-system doesn't use brackets, it contains only one branch:

In[2]:=

Out[2]=

Run a simple L-system with brackets for one iteration:

In[3]:=

Out[3]=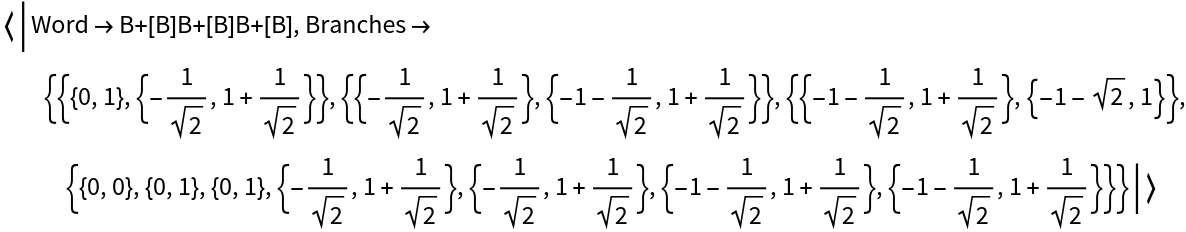

Because this L-system uses brackets, it contains multiple branches:

In[4]:=

Out[4]=

Show a fractal:

In[5]:=

Out[5]=

Show a tree:

In[6]:=

branches = Lookup[ResourceFunction[
"LSystem"][{"G" -> "F+[[G]-G]-F[-FG]+G", "F" -> "FF"}, "G", 5, 22.5], "Branches"];
Graphics[Line[branches]]

Out[6]=

Scope (2)

Display a variety of fractals:

In[7]:=

$fractals = {{"32-segment curve", {{"F" -> "-F+F-F-F+F+FF-F+F+FF+F-F-FF+FF-FF+F+F-FF-F-F+FF-F-F+F+F-F+"}, "F+F+F+F", 2, 90}}, {"Box fractal", {{"F" -> "F-F+F+F-F"}, "F-F-F-F", 4, 90}}, {"Dragon curve", {{"X" -> "X+YF+", "Y" -> "-FX-Y"}, "FX", 11, 90}}, {"Hilbert curve", {{"L" -> "+RF-LFL-FR+", "R" -> "-LF+RFR+FL-"}, "L", 5, 90}}, {"Hilbert curve II", {{"X" -> "XFYFX+F+YFXFY-F-XFYFX", "Y" -> "YFXFY-F-XFYFX+F+YFXFY"}, "X", 3, 90}}, {"Koch snowflake", {{"F" -> "F+F--F+F"}, "F--F--F", 4, 60}}, {"Peano curve", {{"F" -> "F+F-F-F-F+F+F+F-F"}, "F", 3, 90}}, {"Peano-Gosper curve", {{"X" -> "X+YF++YF-FX--FXFX-YF+", "Y" -> "-FX+YFYF++YF+FX--FX-Y"}, "FX", 4, 60}}, {"Quadratic Koch island", {{"F" -> "F-F+F+FFF-F-F+F"}, "F+F+F+F", 3, 90}}, {"Siepiński sieve", {{"F" -> "FF", "X" -> "--FXF++FXF++FXF--"}, "FXF--FF--FF", 5, 60}}, {"Sierpiński arrowhead", {{"X" -> "YF+XF+Y", "Y" -> "XF-YF-X"}, "YF", 6, 60}}, {"Sierpiński curve", {{"X" -> "XF-F+F-XF+F+XF-F+F-X"}, "F+XF+F+XF", 5, 90}}}; With[{name = First@#, fractal = ResourceFunction["LSystem"] @@ Last@#}, Graphics[Line[fractal["Branches"]], PlotLabel -> Style[name, Bold]] ] & /@ fractals$

Out[7]=

Plot different trees:

In[8]:=

plants = {{"Plant 1", {{"F" -> "FF", "G" -> "FG[-F[G]-G][G+G][+F[G]+G]"}, "G", 4, 22.5}}, {"Plant 2", {{"G" -> "F+[[G]-G]-F[-FG]+G", "F" -> "FF"}, "G", 5, 22.5}}, {"Plant 3", {{"F" -> "FF+[+F-F-F]-[-F+F+F]"}, "F", 4, 22.5}}, {"Plant 4", {{"G" -> "F[+FFG][G]-FG", "F" -> "FF"}, "G", 6, 22.5}}, {"Plant 5", {{"G" -> "F[-G]F[+G]-G", "F" -> "FF"}, "G", 6, 20}}, {"Plant 6", {{"G" -> "F[-G][+G]FG", "F" -> "FF"}, "G", 7, 25.7}}};
With[{name = First@#, plant = ResourceFunction["LSystem"] @@ Last@#},
Graphics[Line[plant["Branches"]], PlotLabel -> Style[name, Bold]]
] & /@ plants

Out[8]=

Options (3)

InitialAngle (1)

Show the effect of changing the initial angle:

In[9]:=

Graphics[Line /@ ResourceFunction[
"LSystem"][{"F" -> "FF", "X" -> "--FXF++FXF++FXF--"}, "FXF--FF--FF", 5, 60, "InitialAngle" -> #]["Branches"]] & /@ {0,
45, 90, 135, 180}

Out[9]=

In[10]:=

Out[10]=

InitialPoint (1)

Show the effect of changing the initial point:

In[11]:=

Graphics[Line /@ ResourceFunction[
"LSystem"][{"X" -> "X+YF++YF-FX--FXFX-YF+", "Y" -> "-FX+YFYF++YF+FX--FX-Y"}, "FX", 3, 60, "InitialPoint" -> #]["Branches"], Axes -> True] & /@ RandomInteger[{-10, 10}, {5, 2}]

Out[11]=

In[12]:=

Out[12]=

MoveLength (1)

Show the effect of using different values for "MoveLength":

In[13]:=

Block[{branches, allSegments, segmentsLengths},
branches = ResourceFunction["LSystem"][{"X" -> "YF+XF+Y", "Y" -> "XF-YF-X"}, "YF", 5, 60, "MoveLength" -> #]@"Branches";
allSegments = Partition[Flatten[branches, 1] // DeleteDuplicates, 2, 1];
segmentsLengths = EuclideanDistance @@ # & /@ allSegments;
Grid[{
Style[#, Bold] & /@ {"Plot", "MoveLength", "Segments length average"},
{Graphics[Line /@ branches, Axes -> True, ImageSize -> Small], #,
N@Mean@segmentsLengths}
}, Frame -> All]
] & /@ RandomInteger[{1, 10}, 4]

Out[13]=

Applications (6)

Show the step-by-step creation of the dragon curve:

In[14]:=

dragonCurve = ResourceFunction["LSystem"][{"X" -> "X+YF+", "Y" -> "-FX-Y"}, "FX", 10, 90, "InitialAngle" -> 0]@"Branches" // First; segments = Partition[dragonCurve, 2, 1];
segments = If[#[[1]] != #[[-1]], #, Missing[]] & /@ segments;
segments = segments // DeleteMissing;
graphics = Graphics[{Thick, Pink, Line[segments[[1 ;; #]]]}, ImageSize -> Medium] & /@ Range[2, Length@segments];

In[15]:=

Out[15]=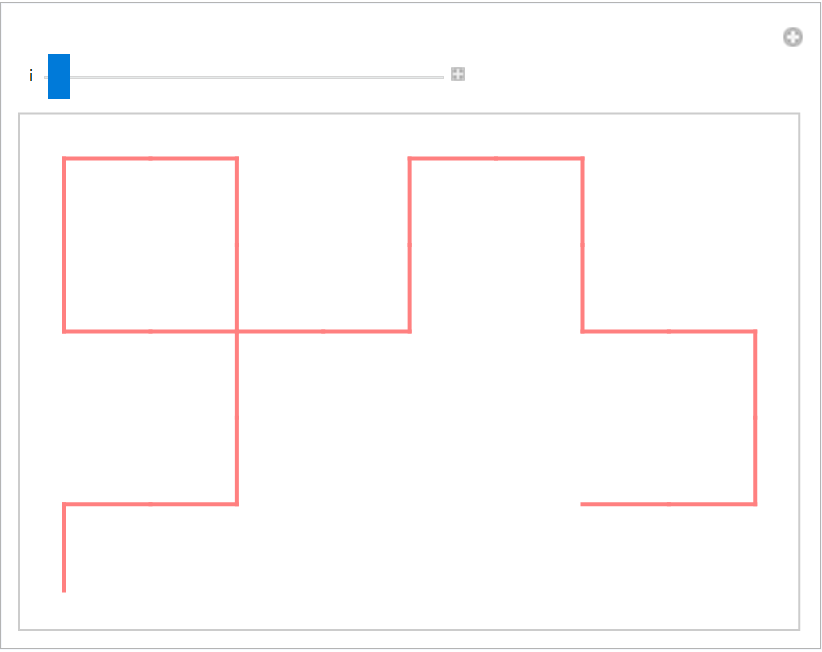

Show the step-by-step creation of the Peano curve:

In[16]:=

peanoCurve = ResourceFunction["LSystem"][{"F" -> "F+F-F-F-F+F+F+F-F"}, "F", 3, 90,
"InitialAngle" -> 0]@"Branches" // First; segments2 = Partition[peanoCurve, 2, 1];
segments2 = If[#[[1]] != #[[-1]], #, Missing[]] & /@ segments2;
segments2 = segments2 // DeleteMissing;
graphics2 = Graphics[{Thick, Pink, Line[segments2[[1 ;; #]]]}, ImageSize -> Medium] & /@ Range[2, Length@segments2];

In[17]:=

Out[17]=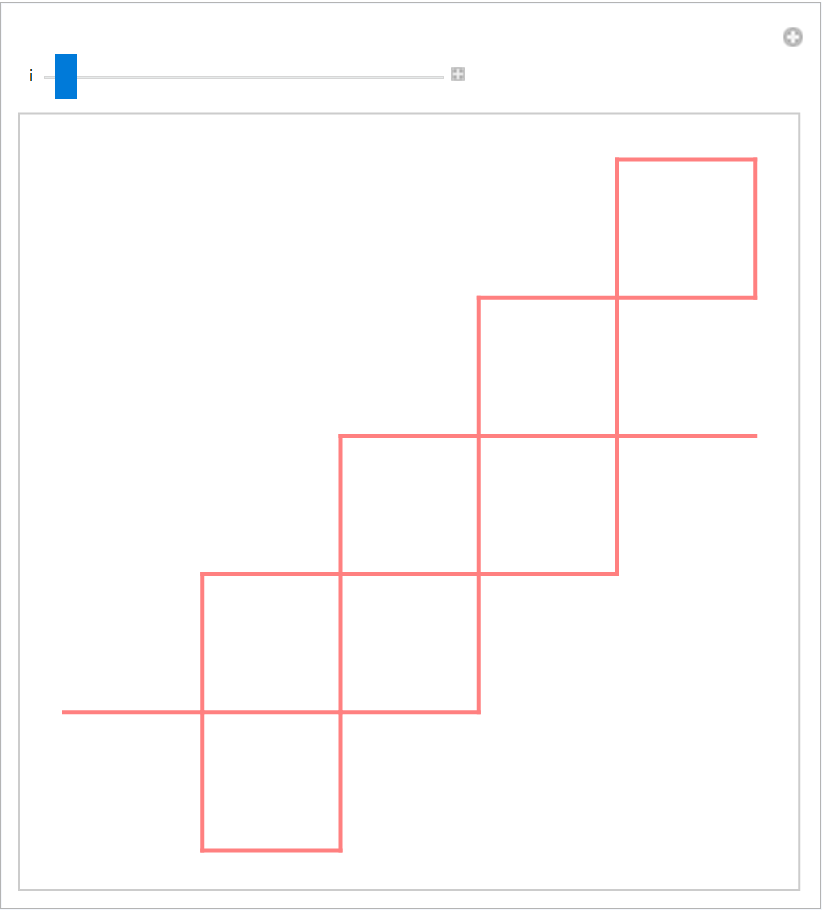

Create a colorful tree:

In[18]:=

Out[18]=

Create a tree with green leaves:

In[19]:=

plantWithLeaves = ResourceFunction["LSystem"][{"G" -> "F[-G]F[+G]-G", "F" -> "FF"}, "G", 6, 20]@"Branches";
leafPoints = Last /@ plantWithLeaves;
leaves = Disk[#, 0.7] & /@ leafPoints;
Graphics[{Thick, Brown, Line /@ plantWithLeaves, Green, leaves}]

Out[19]=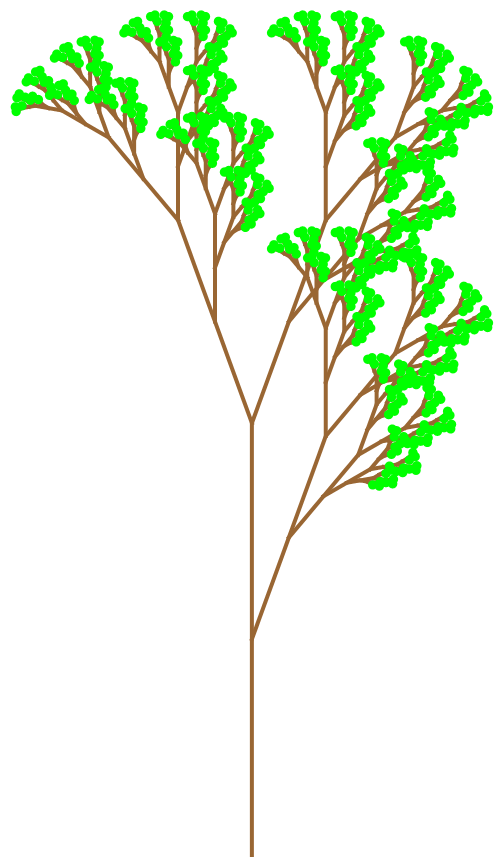

Create a colorful plant with leaves:

In[20]:=

colorfulPlantWithLeaves = ResourceFunction[
"LSystem"][{"F" -> "FF", "G" -> "FG[-F[G]-G][G+G][+F[G]+G]"}, "G",
4, 22.5]@"Branches";
colorfulPlantLeafPoints = Last /@ colorfulPlantWithLeaves;
colorfulPlantLeaves = {RandomColor[], Disk[#, 0.5]} & /@ colorfulPlantLeafPoints;
Graphics[{Thick, {RandomColor[], Line@#} & /@ colorfulPlantWithLeaves,
colorfulPlantLeaves}]

Out[20]=

Create a colorful tree with grapes:

In[21]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/37a87474-7ec5-4ccb-9f2c-5395f804f8f0"]

Out[21]=

Possible Issues (1)

The execution time tends to grow very fast according to the number of iterations:

In[22]:=

Out[22]=

In[23]:=

Out[23]=

Neat Examples (2)

An animated orange tree:

In[24]:=

In[25]:=

plant = ResourceFunction[
"LSystem"][{"G" -> "F+[[G]-G]-F[-FG]+G", "F" -> "FF"}, "G", 4, 22.5]@"Branches";
plantOrangePoints = Last /@ plant;
plantOrangePoints = SortBy[plantOrangePoints, Last];
plantOranges = {RandomChoice[orangeColors], , Disk[#, RandomChoice[{.3, .4, .5}]]} & /@ plantOrangePoints;
plantSegments = Flatten[Partition[#, 2, 1] & /@ plant, 1] // DeleteDuplicates;
plantSegments = SortBy[plantSegments, {First, Last}];
plantSegments = Select[plantSegments, #[[1]] != #[[-1]] &];
plantGraphic = Flatten[{RandomChoice[greenColors], Line@#} & /@ plantSegments];
plantGraphics = {};
AppendTo[plantGraphics, Graphics[Flatten[{plantGraphic, plantOranges[[1 ;; #]]}], Background -> LightBlue]] & /@ Range@Length@plantOranges;

In[26]:=

Out[26]=

Generate a snowflake:

In[27]:=

$angles = N /@ Range[1, 360, 360/5]; fractals = ResourceFunction["LSystem"][{"G" -> "F[-G][+G]FG", "F" -> "FF"}, "G", 2, 45, "InitialAngle" -> #]["Branches"] & /@ angles; Graphics[Flatten[{Thick, Cyan, Line /@ fractals}], Background -> Black]$

Out[27]=

Publisher

Wolfram Summer School

Version History

1.0.0 – 21 June 2021

Source Metadata

Citation:
- De Castro, L. N., Fundamentals of natural computing: Basic Concepts, Algorithms, and Applications. CRC Press, 2006.
- Prusinkiewicz, P., Hanan, J., Lindenmayer Systems, Fractal, and Plants. Springer-Verlag, 1989.
- Prusinkiewicz, P., Lindenmayer, A., The Algorithmic Beauty of Plants. Springer-Verlag, 1990.
- Jacob, C., "Modeling Growth with L-Systems & Mathematica." Mathematica in Education and Research, Volume 4, No. 3, 12–19, 1995. https://pages.cpsc.ucalgary.ca/~jacob/Publications/Publications.html

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

LSystem

Details and Options