Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Kurepa function
ResourceFunction["KurepaK"][z] gives the Kurepa function K(z). |
Evaluate numerically:
| In[1]:= |
| Out[1]= |
Plot over a subset of the reals:
| In[2]:= |
| Out[2]= | 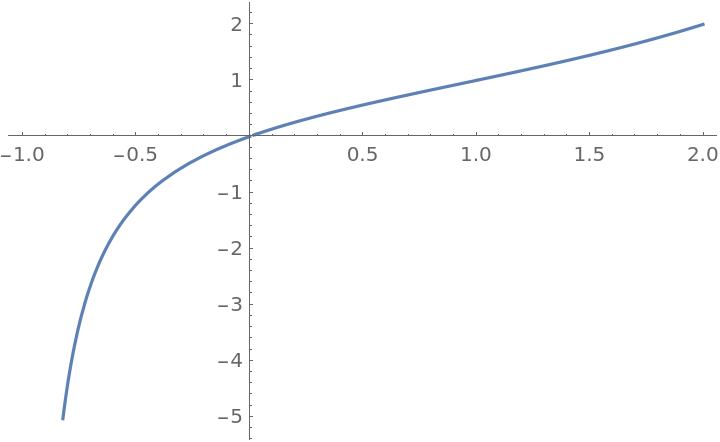 |
Series expansion at the origin:
| In[3]:= |
| Out[3]= |  |
Evaluate for complex arguments:
| In[4]:= |
| Out[4]= |
Evaluate to high precision:
| In[5]:= |
| Out[5]= |
The precision of the output tracks the precision of the input:
| In[6]:= |
| Out[6]= |
KurepaK threads elementwise over lists:
| In[7]:= |
| Out[7]= |
A functional equation satisfied by KurepaK:
| In[8]:= |
| Out[8]= |
Compare KurepaK with its integral representation:
| In[9]:= | ![With[{z = 4/3},
{N[ResourceFunction["KurepaK"][z], 25], NIntegrate[(t^z - 1)/(t - 1) E^-t, {t, 0, \[Infinity]}, WorkingPrecision -> 25]}]](https://www.wolframcloud.com/obj/resourcesystem/images/153/1536b9f1-ba0f-4c30-9d70-d926301f94ac/44df00503792301e.png) |
| Out[9]= |
This work is licensed under a Creative Commons Attribution 4.0 International License