Basic Examples (2)
The points forming a 1st-step Koch curve:
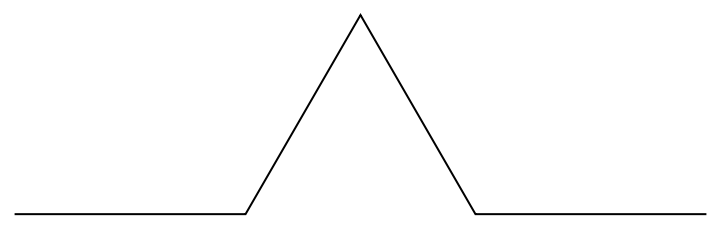
A 1st-step Koch curve visualization:
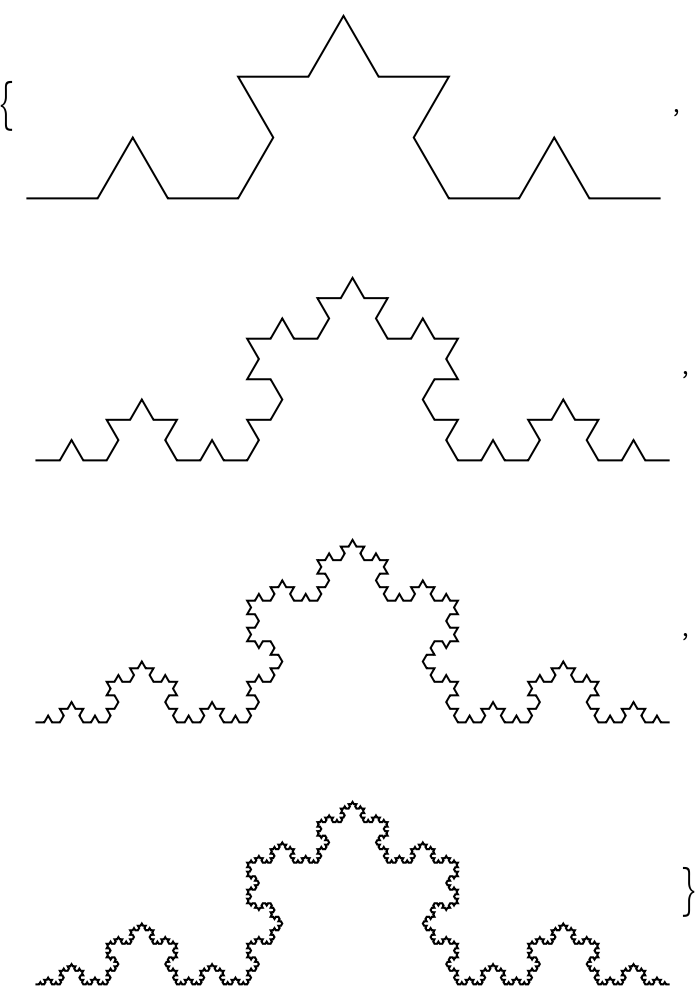
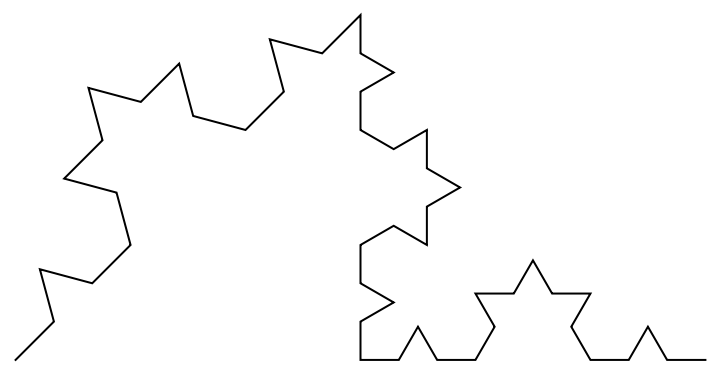
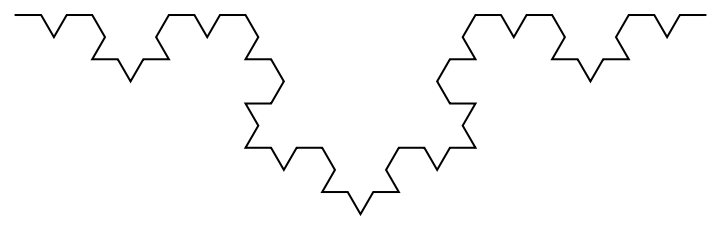
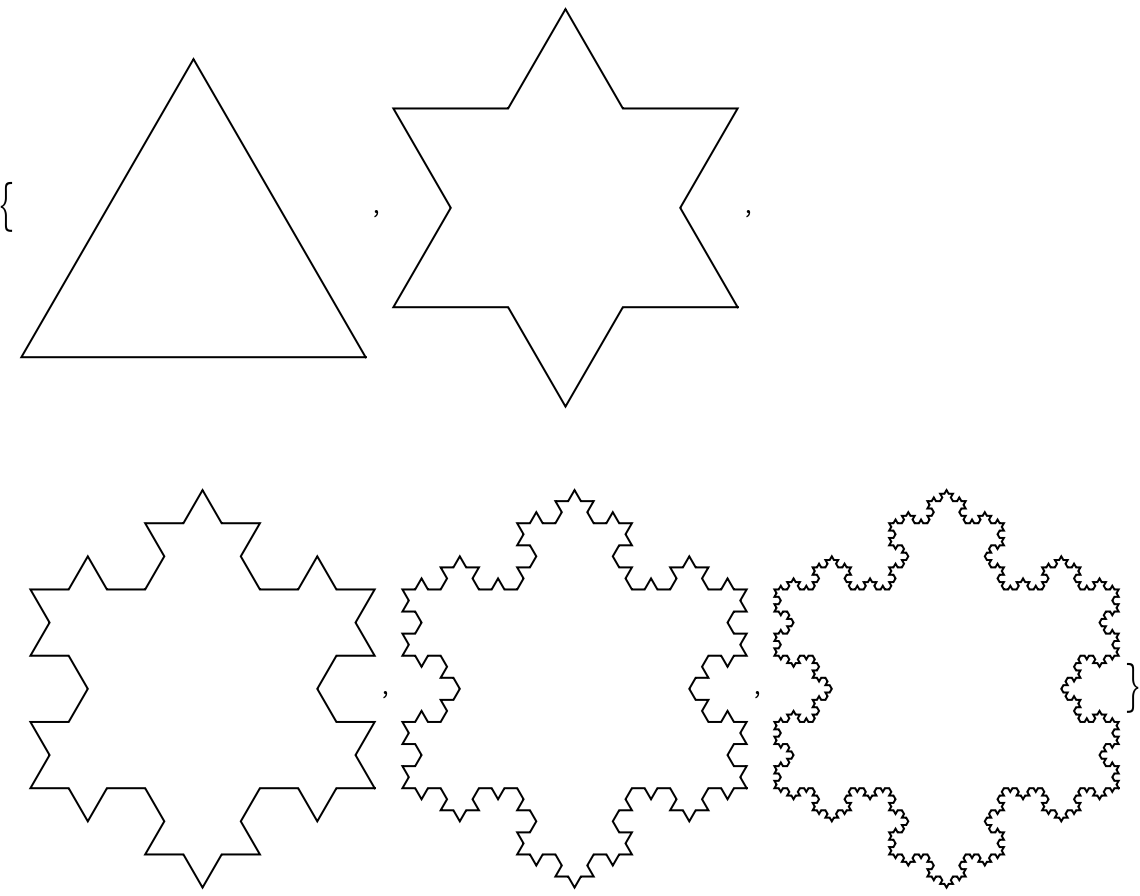
Visualizations of the 2nd through 5th-step Koch curves:
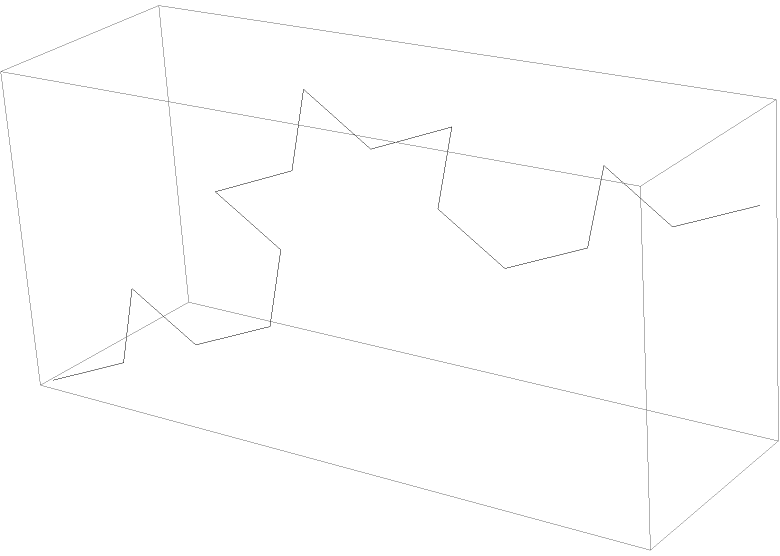
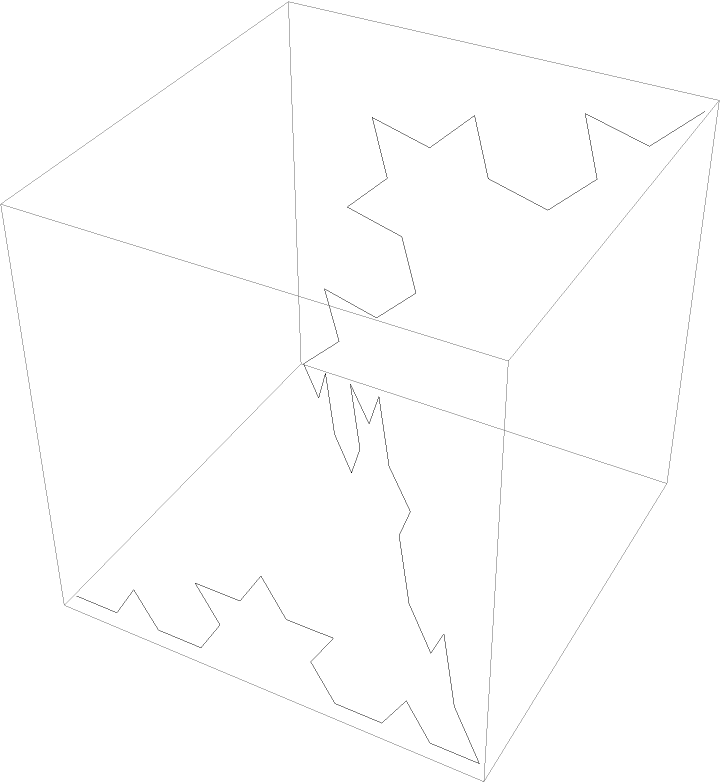
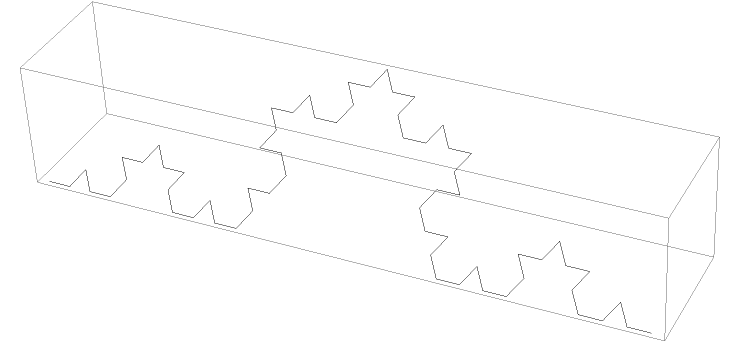
A 2nd-step Koch curve in 3 dimensions:
Scope (5)
Form Koch curves over a 2D list of points:
Form Koch curves over a 3D list of points:
Change the path direction of the 2D Koch curve:
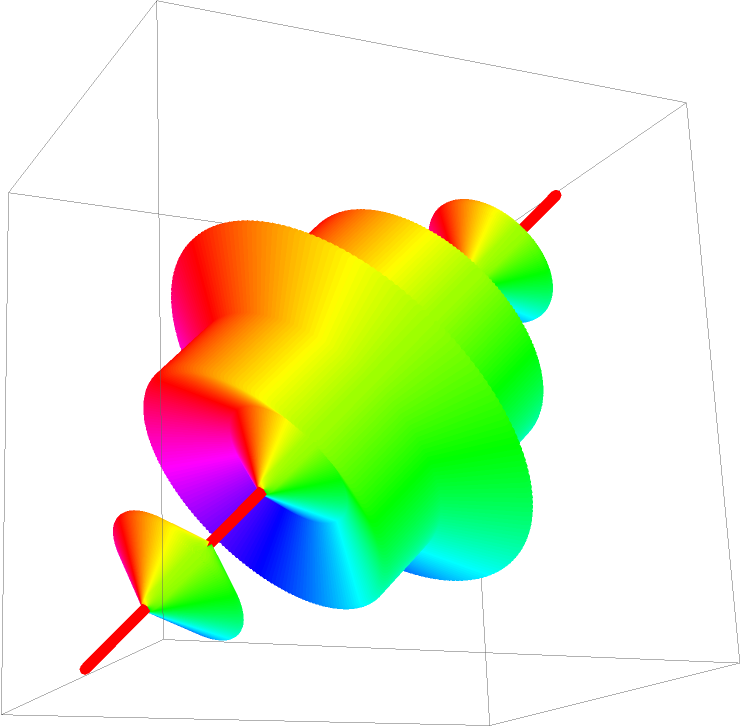
Change the path angle of the 3D Koch curve:
A representation of how the angle rotates the 3D Koch curve, where the 0 angle is in black:
The 0th-step Koch Curve does not introduce any new points:
Options (2)
Setting "ExactValues" to False causes the output to be imprecise:
Imprecise outputs are much faster to compute:
Applications (2)
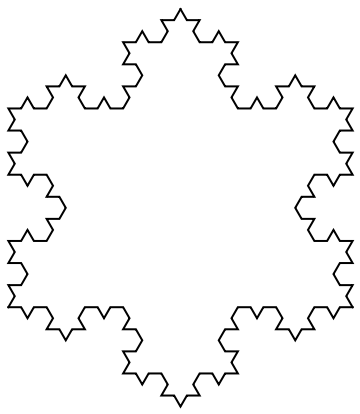
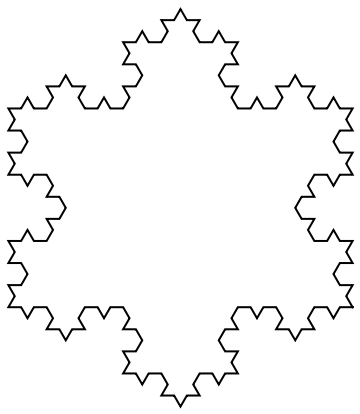
Form a Koch snowflake by specifying the corner points:
Invert the Koch snowflake:
A matrix of the first six steps of Koch snowflakes from the first six regular polygons:
Properties and Relations (1)
The Koch snowflake can be generated with either KochCurve or KochCurvePoints:
Possible Issues (1)
If a point or the value of the orientation is inexact, then parts of the output will return inexact:
Neat Examples (4)
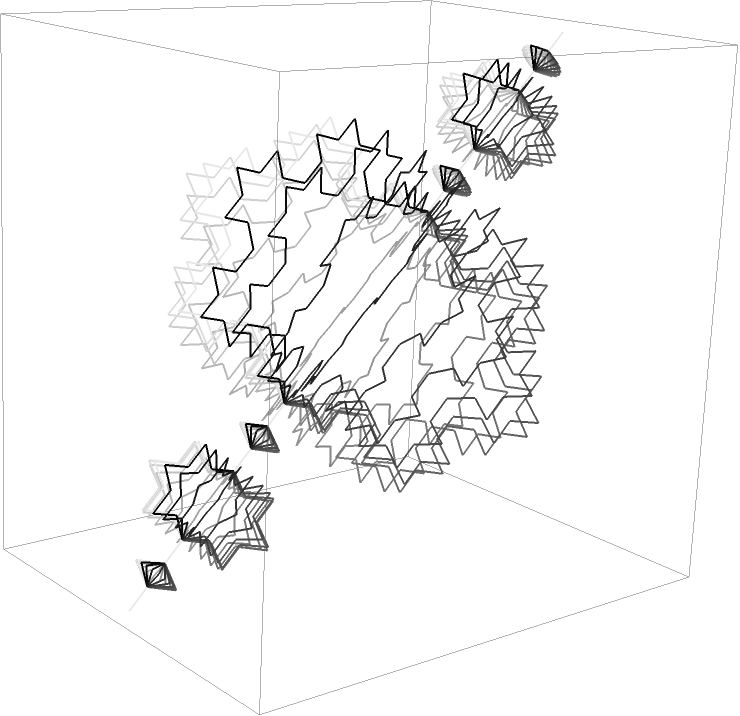
Increasing the density of lines gives the impression of a solid object:
Visualize the increasing detail of higher-step Koch curves:
Apply the Koch Curve to other named curves:
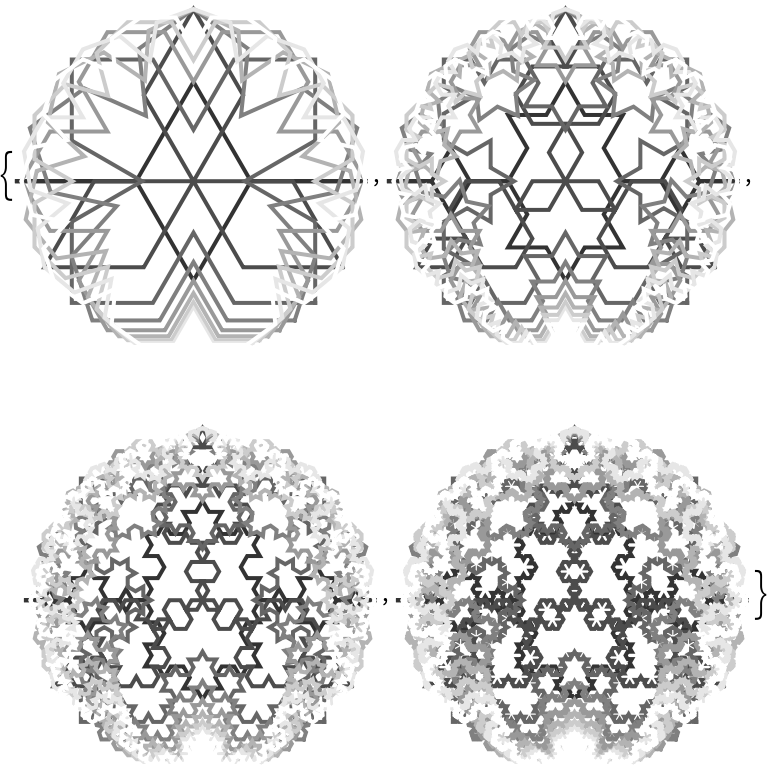
An overlap of the Koch Snowflakes generated from the first 10 regular polygons:
The same Koch Snowflakes when the orientation is reversed:
![Graphics3D[
Table[{Thick, GrayLevel[t/21], Line[ResourceFunction["KochCurvePoints"][3, {{0, 0, 0}, {1, 0, 1}},
N[2 \[Pi] t/20]]]}, {t, 0, 19}]]](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a7a2196-1aef-48d5-bc58-4ce34ef79941/4b480a001bc258c7.png)
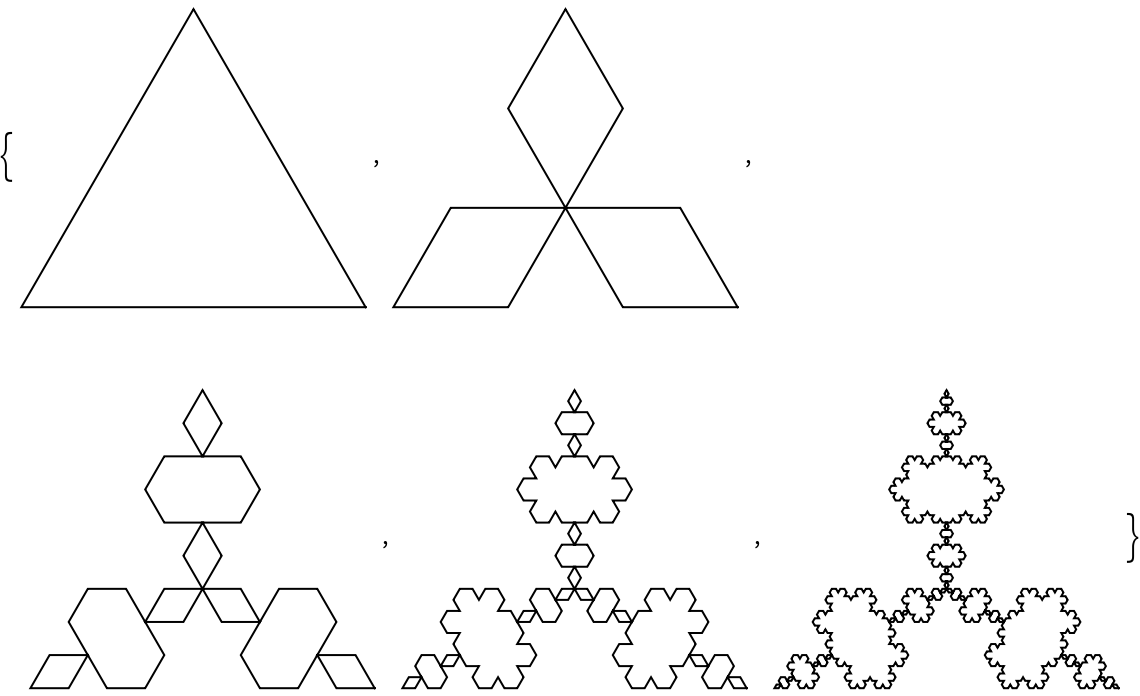
![TableForm[
Array[Graphics[
Line[ResourceFunction["KochCurvePoints"][#1, #2, "ExactValues" -> False]], ImageSize -> 50] &, {6, 6}, {0, 3}]]](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a7a2196-1aef-48d5-bc58-4ce34ef79941/21ef2f2429ac4963.png)

![Graphics[
GeometricTransformation[
KochCurve[3], {RotationTransform[Pi, {1/2, 0}], RotationTransform[-Pi/3, {1, 0}], RotationTransform[Pi/3, {0, 0}]}], ImageSize -> Small]](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a7a2196-1aef-48d5-bc58-4ce34ef79941/4e3bc4debf435b73.png)
![Graphics3D[
Table[{Thickness[0.015], Hue[t/20], Line[ResourceFunction["KochCurvePoints"][2, {{0, 0, 0}, {1, 0, 1}},
N[2 \[Pi] t/20]]]}, {t, 0, 20, 0.1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a7a2196-1aef-48d5-bc58-4ce34ef79941/0f9070c06157f673.png)
![Graphics[
Table[{Thickness[3/1000], GrayLevel[k/6], Line[ResourceFunction["KochCurvePoints"][
k, {{0, 0}, {1, 0}}]]}, {k, 6, 1, -1}], ImageSize -> Large]](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a7a2196-1aef-48d5-bc58-4ce34ef79941/067da9e5fd345a59.png)

![Graphics[
Line[ResourceFunction["KochCurvePoints"][2, First[#], "ExactValues" -> False]]] & /@ {HilbertCurve[4], SierpinskiCurve[3], PeanoCurve[3]}](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a7a2196-1aef-48d5-bc58-4ce34ef79941/3ad7d17e9a8cc2b4.png)

![Graphics[
Table[{Thick, GrayLevel[i/10], Line[ResourceFunction["KochCurvePoints"][#, i, "ExactValues" -> False]]}, {i, 2, 10}]] & /@ {1, 2, 3, 4}](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a7a2196-1aef-48d5-bc58-4ce34ef79941/60381b8257904845.png)

![Graphics[
Table[{Thick, GrayLevel[i/10], Line[ResourceFunction["KochCurvePoints"][#, i, "Down", "ExactValues" -> False]]}, {i, 2, 10}]] & /@ {1, 2, 3, 4}](https://www.wolframcloud.com/obj/resourcesystem/images/5a7/5a7a2196-1aef-48d5-bc58-4ce34ef79941/4085e9c752238372.png)