Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the solution of the standard Kepler equation
ResourceFunction["KeplerE"][ε,M] gives the principal solution E in the standard Kepler equation M=E-ε sin(E). |
Evaluate numerically:
| In[1]:= |
| Out[1]= |
Plot over a subset of the reals:
| In[2]:= |
| Out[2]= | 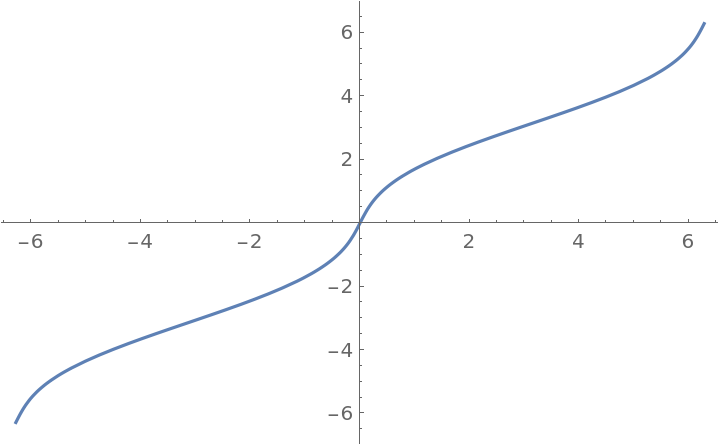 |
Simple exact values are generated automatically:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
Evaluate to arbitrary precision:
| In[5]:= |
| Out[5]= |
The precision of the output tracks the precision of the input:
| In[6]:= |
| Out[6]= |
KeplerE threads elementwise over lists:
| In[7]:= |
| Out[7]= |
Parity transformation is automatically applied:
| In[8]:= |
| Out[8]= |
Compute the distance from the Sun and true anomaly of Mars on a given date, assuming a Keplerian orbit:
| In[9]:= | ![date = DateObject[{2020, 8, 5, 0, 0, 0}];
\[CurlyEpsilon] = PlanetData["Mars", "Eccentricity"];
(* mean anomaly *)
\[ScriptCapitalM] = QuantityMagnitude[
UnitConvert[
DateDifference[PlanetData["Mars", "PeriapsisTimeLast"], date, "Days"] PlanetData["Mars", "MeanMotion"], "Radians"]];
(* eccentric anomaly *)
\[ScriptCapitalE] = ResourceFunction["KeplerE"][\[CurlyEpsilon], \[ScriptCapitalM]];
(* radius vector and true anomaly *)
{PlanetData["Mars", "MajorAxis"] (1 - \[CurlyEpsilon] Cos[\[ScriptCapitalE]]), UnitConvert[
Quantity[
2 ArcTan[
Sqrt[(1 + \[CurlyEpsilon])/(1 - \[CurlyEpsilon])]
Tan[\[ScriptCapitalE]/2]], "Radians"], "ArcMinutes"]}](https://www.wolframcloud.com/obj/resourcesystem/images/b5c/b5c8ed9f-ccca-46af-ac3a-399fe26020ac/16359882536ac73a.png) |
| Out[9]= |
KeplerE is the inverse of the function E-ε sin(E):
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
Visualize the weekly orbital progress of an orbiting body with eccentricity ![]() over a period of one year:
over a period of one year:
| In[12]:= | ![With[{n = 52, \[CurlyEpsilon] = Sqrt[1/2]}, Graphics[{Table[{RandomChoice[ColorData[113, "ColorList"]], Polygon[Prepend[
KeplerOrbit[#, \[CurlyEpsilon]] & /@ Range[w, w + 2 \[Pi]/n, 2 \[Pi]/(7 n)], {0, 0}]]}, {w, \[Pi]/
n, \[Pi] (2 - 1/n), 2 \[Pi]/n}]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/b5c/b5c8ed9f-ccca-46af-ac3a-399fe26020ac/33c6344c7c5252da.png) |
| Out[12]= | 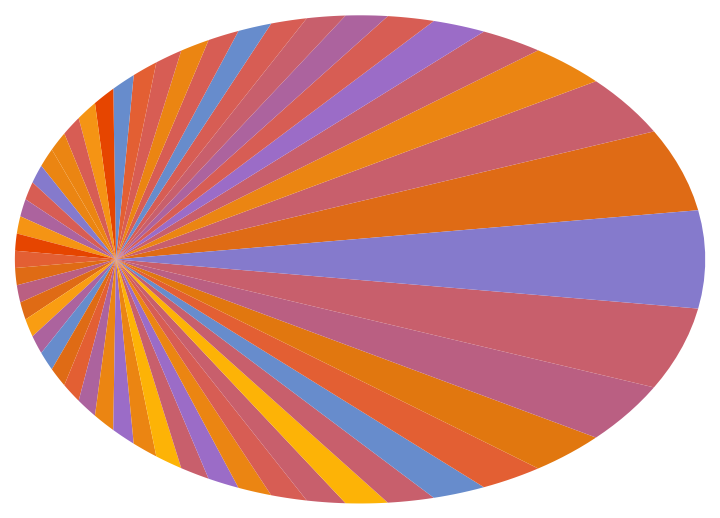 |
This work is licensed under a Creative Commons Attribution 4.0 International License