Properties and Relations (3)
The Johnson circles are closely related to the circumcircle and orthocenter of the reference triangle:
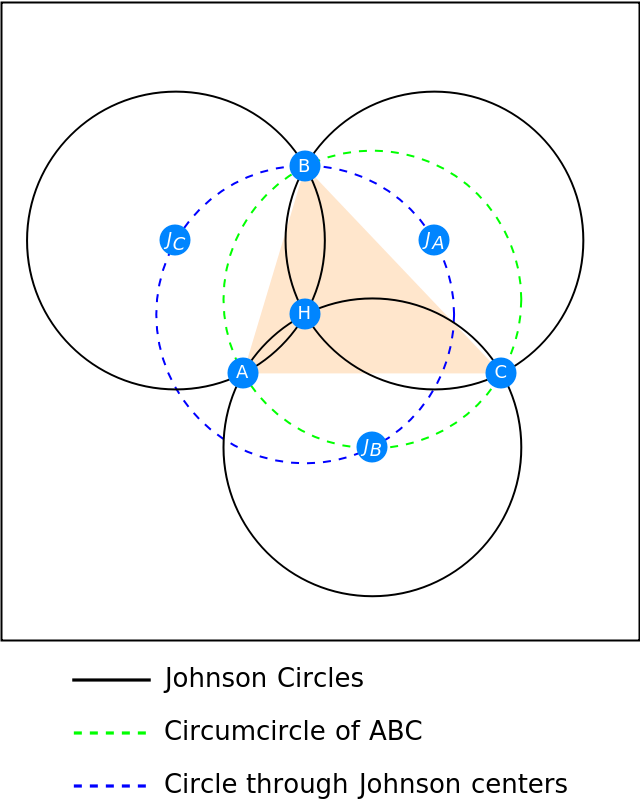
The three Johnson circles are congruent to the circumcircle of the reference triangle:
The three Johnson circles are congruent to the circle that passes through the centers of the three Johnson circles:
The three Johnson circles meet at the orthocenter of the reference triangle:
Visualize the five congruent circles in one diagram with the reference triangle:
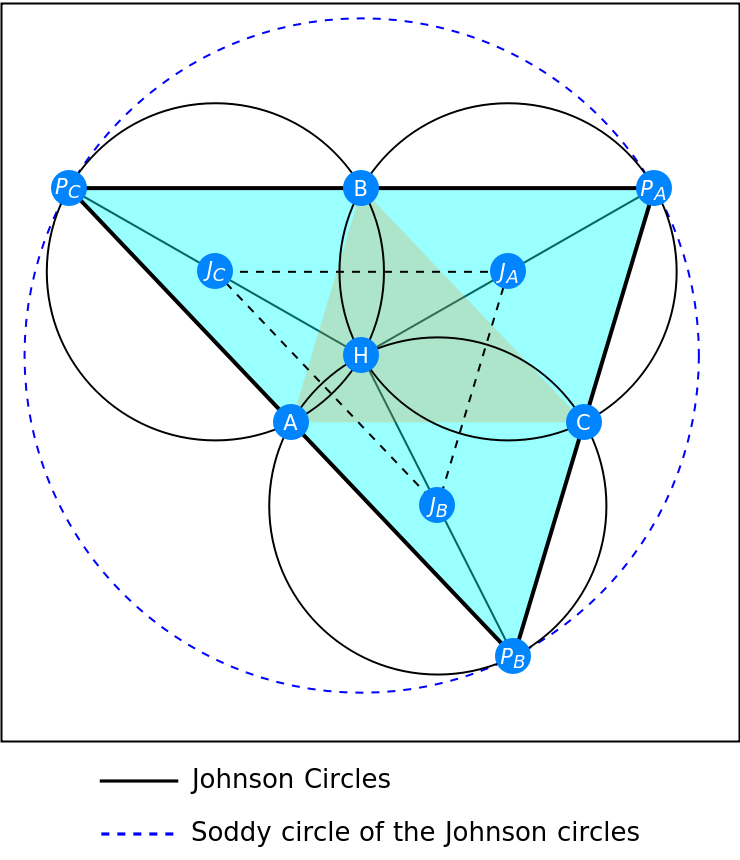
The Soddy circle for the three Johnson circles is the circumcircle of PAPBPC, the anticomplementary triangle of the reference triangle ABC:
Use ScalingTransform function to verify the homothety relation between triangle JAJBJC and PAPBPC:
Compare to the antimedial triangle:
Therefore, the triangle PAPBPC is the dilation of JAJBJC by a factor of two from the orthocenter H of the reference triangle (as the center of similitude):
Because both triangle ABC and JAJBJC are similar to PAPBPC with contracting scaling factor of 1/2, the two triangles are in fact congruent to each other:
The Johnson triangle and its reference triangle share the same nine-point center, the same Euler line and the same radius for nine-point circle:
![tri = {{0, 0}, {1.2, 4}, {5, 0}};
orthoCen = TriangleCenter[tri, "Orthocenter"];
jcs = ResourceFunction["JohnsonCircles"][tri]](https://www.wolframcloud.com/obj/resourcesystem/images/14d/14dadb19-8349-4f33-a1ab-3efb2ee1c4c5/6e3d9b503910dfe1.png)
![labelFun[v1_, v2_] := {
PointSize[Scaled[0.05`]], Hue[0.58`, 1, 1], Point[v1], Text[Style[v2, White, FontSize -> Scaled[0.03`]], v1]};
(* visualize 5 congruent circles together with the reference triangle *)
Legended[
Module[{or = TriangleCenter[tri, "Orthocenter"]},
Graphics[{
{Orange, Opacity[0.2`], Triangle[tri]},
{Dashed, Green, refCircum},
{Dashed, Blue, johnsonCenterCircum},
jcs,
labelFun[or, "H"],
MapThread[
labelFun, {jcs[[All, 1]], {"\!\(\*SubscriptBox[\(J\), \(A\)]\)",
"\!\(\*SubscriptBox[\(J\), \(B\)]\)", "\!\(\*SubscriptBox[\(J\), \(C\)]\)"}}],
MapThread[labelFun, {tri, {"A", "B", "C"}}]
}, PlotRange -> {{-4.5, 7.5}, {-5, 7}}] // Framed],
Placed[
LineLegend[{Black,
Directive[Green, Dashed],
Directive[Blue, Dashed]}, {"Johnson Circles", "Circumcircle of ABC", "Circle through Johnson centers"}], Bottom]]](https://www.wolframcloud.com/obj/resourcesystem/images/14d/14dadb19-8349-4f33-a1ab-3efb2ee1c4c5/7ca706df1203960d.png)
![tri = {{0, 0}, {1.2, 4}, {5, 0}};
jcs = ResourceFunction["JohnsonCircles"][tri];
jcsTri = Triangle[jcs[[All, 1]]];
orthoCen = TriangleCenter[tri, "Orthocenter"];
anti = TriangleConstruct[tri, "AntimedialTriangle"];](https://www.wolframcloud.com/obj/resourcesystem/images/14d/14dadb19-8349-4f33-a1ab-3efb2ee1c4c5/0a42127c474ac095.png)
![labelFun[v1_, v2_] := {
PointSize[Scaled[0.05`]], Hue[0.58`, 1, 1], Point[v1], Text[Style[v2, White, FontSize -> Scaled[0.03`]], v1]};
(* visualize 5 congruent circles together with the reference triangle *)
Legended[
Module[{or = TriangleCenter[tri, "Orthocenter"]},
Graphics[{
Sequence[
Map[Line[{orthoCen, #}]& ,
Part[anti, 1]], {
Opacity[0.4],
EdgeForm[Thick], Cyan, anti}, {Orange,
Opacity[0.2],
Triangle[tri]}, {Transparent,
EdgeForm[Dashed], jcsTri}, {Dashed, Blue,
TriangleConstruct[anti, "Circumcircle"]}, jcs,
labelFun[or, "H"],
MapThread[labelFun, {
Part[jcsTri, 1], {"\!\(\*SubscriptBox[\(J\), \(A\)]\)", "\!\(\*SubscriptBox[\(J\), \(B\)]\)", "\!\(\*SubscriptBox[\(J\), \(C\)]\)"}}],
MapThread[labelFun, {tri, {"A", "B", "C"}}],
MapThread[labelFun, {
Part[anti, 1], {"\!\(\*SubscriptBox[\(P\), \(A\)]\)", "\!\(\*SubscriptBox[\(P\), \(B\)]\)", "\!\(\*SubscriptBox[\(P\), \(C\)]\)"}}]]
}, PlotRange -> {{-4.8, 7.5}, {-5.3, 7}}] // Framed],
Placed[
LineLegend[{Black,
Directive[Blue, Dashed]}, {"Johnson Circles", "Soddy circle of the Johnson circles"}], Bottom]]](https://www.wolframcloud.com/obj/resourcesystem/images/14d/14dadb19-8349-4f33-a1ab-3efb2ee1c4c5/73981cd3f1385265.png)
![tri = {{0, 0}, {1.2, 4}, {5, 0}};
jcs = ResourceFunction["JohnsonCircles"][tri];
jcsTri = Triangle[jcs[[All, 1]]];](https://www.wolframcloud.com/obj/resourcesystem/images/14d/14dadb19-8349-4f33-a1ab-3efb2ee1c4c5/53ef8e1eb6c08262.png)