Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 JacobianMatrix

Source Notebook

Compute the Jacobian matrix of a vector function with respect to a list of variables

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["JacobianMatrix"][expr,{var1,var2,…}]

computes the Jacobian matrix of the expression expr with respect to the given variables.

Examples

Basic Examples (6) 

Compute the Jacobian matrix of an expression:

In[1]:=
ResourceFunction[ "JacobianMatrix", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{4 x^2 y, x - y^2}, {x, y, z}]
Out[1]=

Compute the Jacobian matrix of another expression:

In[2]:=
ResourceFunction[ "JacobianMatrix", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{4 x^2 y, x - y^2}, {x, y}] // MatrixForm
Out[2]=

Compute the Jacobian matrix of another expression:

In[3]:=
ResourceFunction[ "JacobianMatrix", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{r Sin[t], r Cos[t]}, {r, t}]
Out[3]=

Compute the Jacobian matrix of another expression:

In[4]:=
ResourceFunction[ "JacobianMatrix", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{x y z, x^2 z}, {x, y, z}] // MatrixForm
Out[4]=

Compute the Jacobian matrix of another expression:

In[5]:=
ResourceFunction[ "JacobianMatrix", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{r p Sin[t], r p Cos[t], r^2/p}, {r, p, t}] // MatrixForm
Out[5]=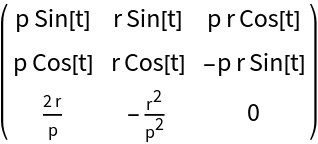

Compute the Jacobian matrix of another expression:

In[6]:=
ResourceFunction[ "JacobianMatrix", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{r Cos[t], r Sin[t]}, {r, t}]
Out[6]=

Properties and Relations (3) 

Compute the Jacobian matrix of an expression:

In[7]:=
ResourceFunction[ "JacobianMatrix", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{x^3 - 2 x y - y^6, x - y^2}, {x, y}]
Out[7]=

Take the determinant of this result:

In[8]:=
Det[%]
Out[8]=

Compare this to the result obtained using ResourceFunction["JacobianDeterminant"]:

In[9]:=
ResourceFunction["JacobianDeterminant"][{x^3 - 2 x y - y^6, x - y^2}, {x, y}]
Out[9]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 4.0.0 – 23 March 2023
  • 3.1.0 – 12 May 2021
  • 3.0.0 – 24 January 2020
  • 2.0.0 – 06 September 2019
  • 1.0.0 – 05 August 2019

Related Resources

License Information