Function Repository Resource:

JacobiShufflePermutations

Generate a set of permutations for Jacobi identities of arbitrary order

Contributed by: Motoharu Ito

ResourceFunction["JacobiShufflePermutations"][k,l]

Find the Jacobi subset of (k,l)-order, where k and l are non-negative integers.

Details

[X₁,…,X_n] represents the bracketed product that extends the Lie bracket product called the left-normed bracket, which is defined recursively by

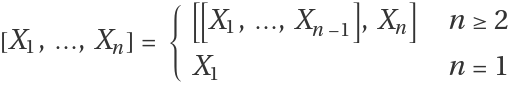
For any Lie algebra, a subset J of the symmetric group S_n is said to be a Jacobi subset if it satisfies

. This identity is also called the n th-order Jacobi identity of J.

A Jacobi subset J can be labeled J_k,l for k+l≤n, and J_k,l is called a Jacobi subset of (k,l)-order.

The explicit expression for J_k,l is represented by the following complex expression. Despite its complexity, it can be organized using the shuffle Sh¹.

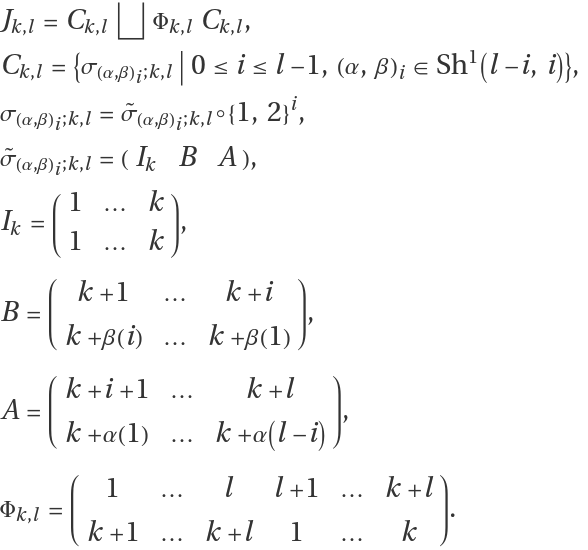
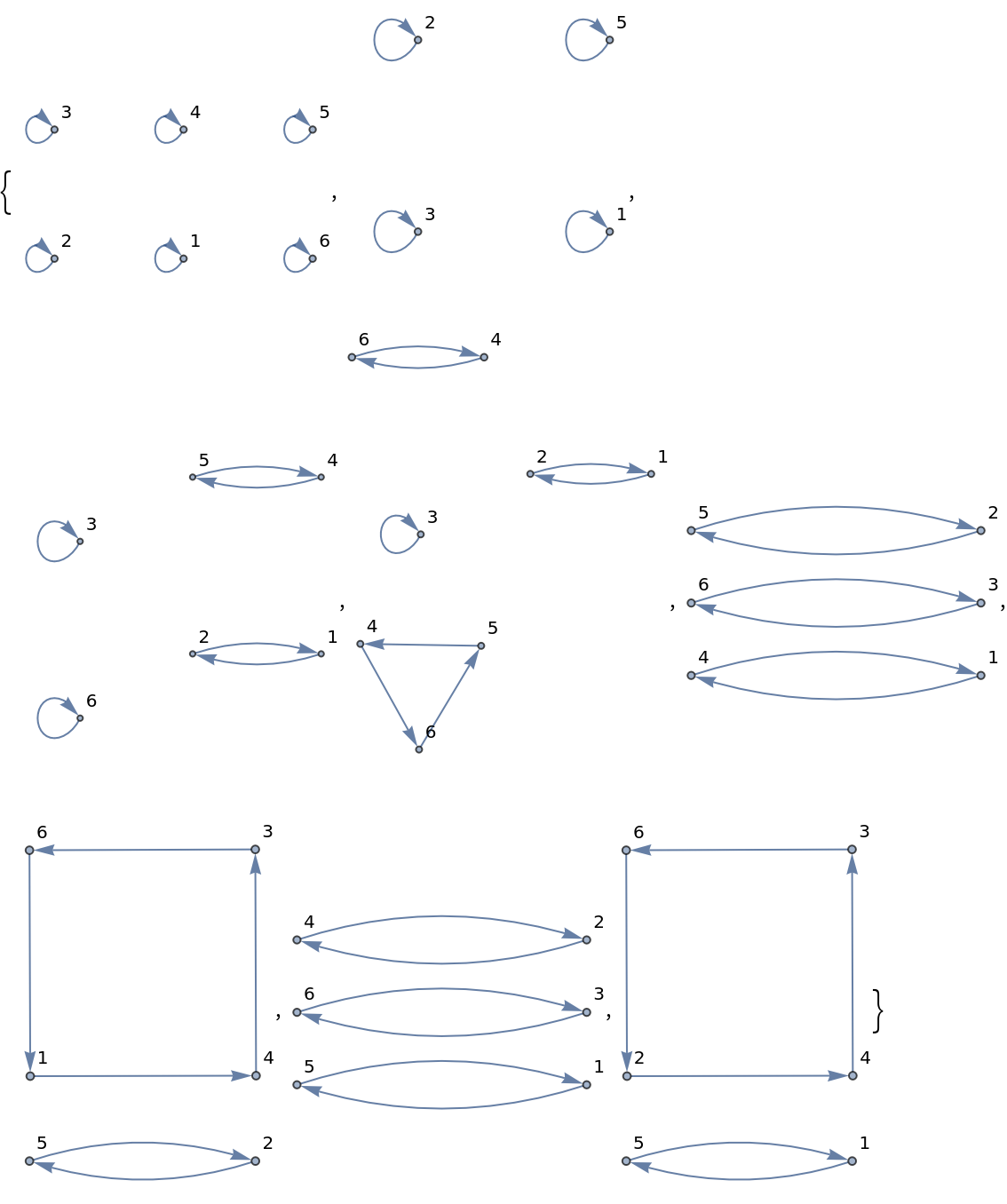
For example, since J_1,1={{1,2},{2,1}} for n=2=1+1, the second-order Jacobi identity is the anti-commutator. And since J_1,2=J_2,1={{1,2,3},{2,3,1},{3,1,2}} for n=3=1+2=2+1, the third-order Jacobi version is the standard Jacobi identity.

Examples

Basic Examples (3)

Give the anti-commutator ([X₁,X₂]+[X₂,X₁]=0) permutations:

In[1]:=

Out[1]=

Give the Jacobi identity ([X₁,X₂,X₃]+[X₂,X₃,X₁]+[X₃,X₁,X₂]=0) permutations:

In[2]:=

Out[2]=

Give the higher Jacobi identity ([X₁,X₂,X₃,X₄]+[X₁,X₄,X₃,X₂]+[X₂,X₃,X₄,X₁]+[X₃,X₁,X₂,X₄]+[X₄,X₁,X₂,X₃]=0) permutations:

In[3]:=

Out[3]=

Scope (3)

Prove the Jacobi identity for a matrix:

In[4]:=

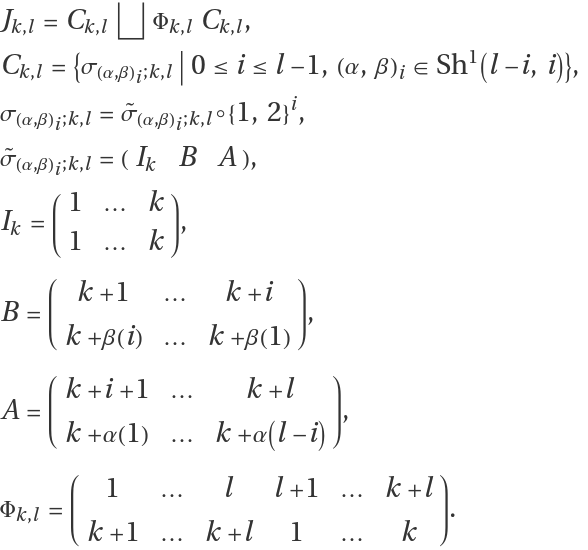
$jacobiator // ClearAll; jacobiator // Attributes = {}; jacobiator[k_, l_, m_] := Module[{MatrixCommutator}, MatrixCommutator[{mm_}] := mm; MatrixCommutator[{a_, b_}] := a . b - b . a; MatrixCommutator[{mm__}] := Fold[MatrixCommutator[{#1, #2}] &][{mm}]; Sum[i, {i, Map[MatrixCommutator[Map[m, #]] &, ResourceFunction["JacobiShufflePermutations"][k, l]]}] // FullSimplify ]; m[k_] := {{Subscript[a, k], Subscript[b, k]}, {Subscript[c, k], Subscript[d, k]}}; {jacobiator[1, 2, m], jacobiator[1, 3, m]} Clear[jacobiator, m];$

Out[8]=