Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 JacobiMatrix

Source Notebook

Generate the Jacobi matrix corresponding to an orthogonal polynomial

Contributed by: Jan Mangaldan

ResourceFunction["JacobiMatrix"][n,poly]

yields the nth order Jacobi matrix corresponding to the orthogonal polynomial pn(x) represented by poly.

Details and Options

A Jacobi matrix is a square tridiagonal matrix whose characteristic polynomial is a scalar multiple of the orthogonal polynomial pn(x).
The argument poly can be any of the following:
"ChebyshevFirst"Chebyshev polynomial of the first kind ChebyshevT[n,x]
"ChebyshevSecond"Chebyshev polynomial of the second kind ChebyshevU[n,x]
"Hermite"Hermite polynomial HermiteH[n,x]
"Laguerre"Laguerre polynomial LaguerreL[n,x]
"Legendre"Legendre polynomial LegendreP[n,x]
{"Gegenbauer",m}Gegenbauer polynomial GegenbauerC[n,m,z]
{"Laguerre",a}associated Laguerre polynomial LaguerreL[n,a,x]
{"Jacobi",a,b}Jacobi polynomial JacobiP[n,a,b,x]
Strings in specifications like "Legendre" and {"Jacobi",a,b} can be replaced with the corresponding built-in symbols, as in LegendreP and {JacobiP,a,b}.
The result of ResourceFunction["JacobiMatrix"] is a SparseArray.
ResourceFunction["JacobiMatrix"][n,poly,"Symmetric"→True] generates a symmetric tridiagonal Jacobi matrix. ResourceFunction["JacobiMatrix"][n,poly,"Symmetric"→False] generates an unsymmetric tridiagonal Jacobi matrix with 1's in the subdiagonal.

Examples

Basic Examples (1) 

The Jacobi matrix corresponding to a Legendre polynomial:

In[1]:=
ResourceFunction["JacobiMatrix"][4, "Legendre"] // MatrixForm
Out[1]=

Scope (2) 

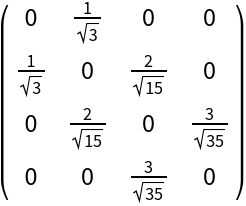
Jacobi matrix of a Jacobi polynomial with symbolic parameters:

In[2]:=
ResourceFunction["JacobiMatrix"][ 3, {"Jacobi", \[Alpha], \[Beta]}] // MatrixForm
Out[2]=

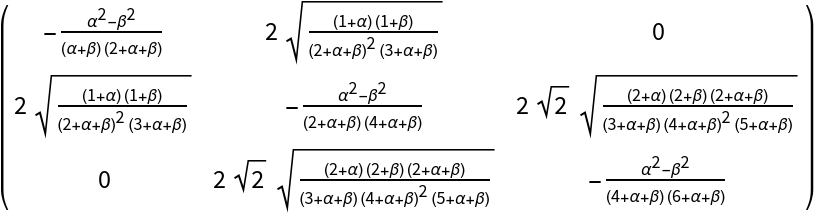
An equivalent specification:

In[3]:=
ResourceFunction["JacobiMatrix"][ 3, {JacobiP, \[Alpha], \[Beta]}] // MatrixForm
Out[3]=

Options (1) 

Symmetric (1) 

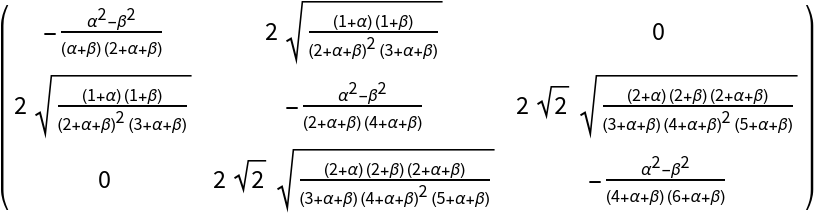
Symmetric and unsymmetric Jacobi matrices for an associated Laguerre polynomial:

In[4]:=
MatrixForm /@ {ResourceFunction["JacobiMatrix"][ 4, {"Laguerre", \[Alpha]}, "Symmetric" -> True], ResourceFunction["JacobiMatrix"][4, {"Laguerre", \[Alpha]}, "Symmetric" -> False]}
Out[4]=

Applications (2) 

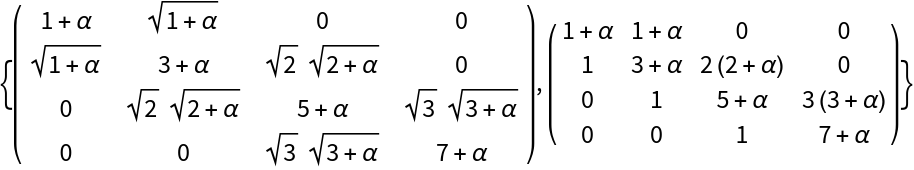
Find the roots of an orthogonal polynomial by computing the eigenvalues of a Jacobi matrix:

In[5]:=
Eigenvalues[ N[ResourceFunction["JacobiMatrix"][4, {"Laguerre", -1/3}]]] // Sort
Out[5]=

Compare with the result of using NSolve:

In[6]:=
x /. NSolve[LaguerreL[4, -1/3, x] == 0, x]
Out[6]=

Properties and Relations (2) 

The characteristic polynomial of a Jacobi matrix is a scalar multiple of the associated orthogonal polynomial:

In[7]:=
CharacteristicPolynomial[ ResourceFunction["JacobiMatrix"][4, "Hermite"], x]
Out[7]=
In[8]:=
#/Coefficient[#, x, Exponent[#, x]] &[HermiteH[4, x]] // Expand
Out[8]=

The unsymmetric and symmetric Jacobi matrices are related to each other through a similarity transformation:

In[9]:=
m1 = ResourceFunction["JacobiMatrix"][4, LaguerreL, "Symmetric" -> True]; m2 = ResourceFunction["JacobiMatrix"][4, LaguerreL, "Symmetric" -> False]; With[{d = FoldList[Times, 1, Normal@Diagonal[m1, 1]]}, m1 == DiagonalMatrix[d] . m2 . DiagonalMatrix[1/d]]
Out[9]=

Version History

  • 1.0.0 – 05 April 2021

Source Metadata

  • Citation:
    • Chihara T.S., An Introduction to Orthogonal Polynomials. New York: Gordon and Breach, 1978.
    • Gautschi W., Orthogonal Polynomials: Computation and Approximation. Oxford: Oxford University Press, 2004.

Related Resources

License Information