Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Determine the iterated logarithm of an input
ResourceFunction["IteratedLog"][z] gives the iterated natural logarithm of z. | |
ResourceFunction["IteratedLog"][b,z] gives the iterated logarithm base b of z. |
IteratedLog is the inverse of tetration (repeated exponentiation):
| In[1]:= |
| Out[1]= |
A slightly larger input shows a step-like jump in the value of IteratedLog:
| In[2]:= |
| Out[2]= |
Make a table of the iterated logarithm of the first 50 integers:
| In[3]:= |
| Out[3]= |
The logarithmic base can be any real number greater than 1:
| In[4]:= |
| Out[4]= |
Plot the iterated logarithm for different logarithmic bases:
| In[5]:= | ![ListLinePlot[{
Table[ResourceFunction["IteratedLog"][i], {i, 0, 30}],
Table[ResourceFunction["IteratedLog"][8, i], {i, 0, 30}],
Table[ResourceFunction["IteratedLog"][20, i], {i, 0, 30}]
}, PlotLegends -> {"iterated natural log", "iterated log base-8", "iterated log base-20"}]](https://www.wolframcloud.com/obj/resourcesystem/images/49d/49d2a848-e22d-4f9c-8f9a-f6dee3e960e4/2b2ca922c2b38f3c.png) |
| Out[5]= | 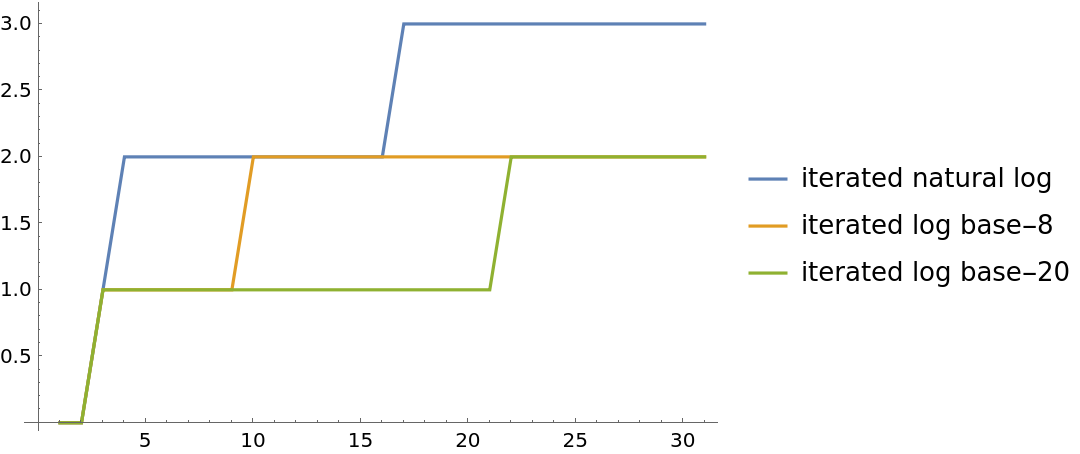 |
IteratedLog will return unevaluated in cases where evaluation might lead to numerical overflow:
| In[6]:= |
| Out[6]= |
This work is licensed under a Creative Commons Attribution 4.0 International License