Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 IteratedFiniteAutomaton

Source Notebook

Iteratively apply a transducer finite automaton

Contributed by: Stephen Wolfram

ResourceFunction["IteratedFiniteAutomaton"][rule,init,t]

generates a list representing the evolution of the iterated finite automaton with the specified rule from initial condition init for t steps.

ResourceFunction["IteratedFiniteAutomaton"][rule,s0,init,t]

starts the iterated finite automaton with state s0.

ResourceFunction["IteratedFiniteAutomaton"][rule,init]

gives the result of evolving init for one step.

ResourceFunction["IteratedFiniteAutomaton"][rule,s0]

is an operator form of IteratedFiniteAutomaton that represents one step of evolution.

Details and Options

The rules for the iterated finite automaton can be given as a list of elements of the form {s,i}→{f,o}, where s is the initial state of the finite automaton, f is the final state, i is the symbol taken as input and o is the symbol given as output.
The rules can also be given as a numerical code in the form {code,{s,k}}, where s is the number of states of the finite automaton, and k is the number of possible symbols used. There are (sk)sk possible rules.
ResourceFunction["IteratedFiniteAutomaton"][rule, init] implements a transducer finite automaton that starts in state 1 at the first symbol in init, then successively reads a symbol and writes a symbol, according to the rule.

Examples

Basic Examples (2) 

Apply a simple iterated finite automaton to a single list:

In[1]:=
ResourceFunction[ "IteratedFiniteAutomaton"][{{1, 1} -> {1, 0}, {1, 0} -> {2, 1}, {2, 1} -> {2, 1}, {2, 0} -> {1, 0}}, {0, 0, 0, 0}]
Out[1]=

Iterate the same rule for 100 steps:

In[2]:=
ArrayPlot[ ResourceFunction[ "IteratedFiniteAutomaton"][{{1, 1} -> {1, 0}, {1, 0} -> {2, 1}, {2, 1} -> {2, 1}, {2, 0} -> {1, 0}}, ConstantArray[0, 100], 100]]
Out[2]=

Scope (3) 

Evolve an iterated finite automaton specified as a code for 2 steps:

In[3]:=
ResourceFunction["IteratedFiniteAutomaton"][{28126, {3, 2}}, CenterArray[{1, 0, 0, 1}, 20], 2]
Out[3]=

Evolve an iterated finite automaton specified as replacement rules for 2 steps:

In[4]:=
ResourceFunction[ "IteratedFiniteAutomaton"][{{1, 1} -> {2, 1}, {1, 0} -> {2, 1}, {2, 1} -> {3, 0}, {2, 0} -> {1, 1}, {3, 1} -> {1, 1}, {3, 0} -> {3, 0}}, CenterArray[{1, 0, 0, 1}, 20], 2]
Out[4]=

Give the result of one step of evolving an iterated finite automaton:

In[5]:=
ResourceFunction["IteratedFiniteAutomaton"][{28126, {3, 2}}, CenterArray[{1, 0, 0, 1}, 20]]
Out[5]=
In[6]:=
ResourceFunction[ "IteratedFiniteAutomaton"][{{1, 1} -> {2, 1}, {1, 0} -> {2, 1}, {2, 1} -> {3, 0}, {2, 0} -> {1, 1}, {3, 1} -> {1, 1}, {3, 0} -> {3, 0}}, CenterArray[{1, 0, 0, 1}, 20]]
Out[6]=

The operator form equivalent:

In[7]:=
ResourceFunction["IteratedFiniteAutomaton"][{28126, {3, 2}}, 1][ CenterArray[{1, 0, 0, 1}, 20]]
Out[7]=
In[8]:=
ResourceFunction[ "IteratedFiniteAutomaton"][{{1, 1} -> {2, 1}, {1, 0} -> {2, 1}, {2, 1} -> {3, 0}, {2, 0} -> {1, 1}, {3, 1} -> {1, 1}, {3, 0} -> {3, 0}}, 1][CenterArray[{1, 0, 0, 1}, 20]]
Out[8]=

Two different ways to specify the same iterated finite automaton:

In[9]:=
{ArrayPlot[ ResourceFunction["IteratedFiniteAutomaton"][{28126, {3, 2}}, ConstantArray[0, 100], 100]], ArrayPlot[ ResourceFunction[ "IteratedFiniteAutomaton"][{{1, 1} -> {2, 1}, {1, 0} -> {2, 1}, {2, 1} -> {3, 0}, {2, 0} -> {1, 1}, {3, 1} -> {1, 1}, {3, 0} -> {3, 0}}, ConstantArray[0, 100], 100]]}
Out[9]=

Applications (1) 

Rostislav Grigorchuk's automaton:

In[10]:=
ArrayPlot[ ResourceFunction["IteratedFiniteAutomaton"][{8950703898, {5, 2}}, RandomInteger[1, 100], 100]]
Out[10]=

Neat Examples (1) 

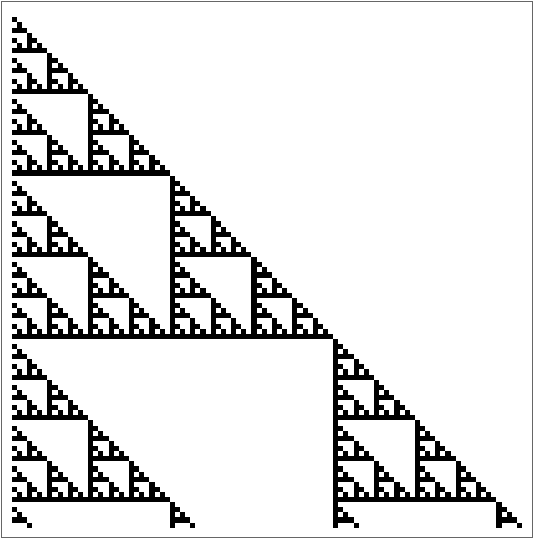
Generate a Sierpiński gasket-like structure:

In[11]:=
ArrayPlot[ ResourceFunction["IteratedFiniteAutomaton"][{54, {2, 2}}, ConstantArray[0, 100], 100]]
Out[11]=

Version History

  • 1.0.0 – 29 June 2020

License Information