Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
A two-argument form of Counts that gives an association between a set of provided keys and the number of times those keys appear in a list
ResourceFunction["ItemCounts"][list,keys] gives an Association that pairs each element of keys with the number of times it appears in list. | |
ResourceFunction["ItemCounts"][list,keys,default] outputs default for any key not appearing in list. | |
ResourceFunction["ItemCounts"][list,assoc] outputs the associated value of a given key in assoc if that key is not an element of list. | |
ResourceFunction["ItemCounts"][assoc] is an operator form of ResourceFunction["ItemCounts"] that produces ResourceFunction["ItemCounts"][list,assoc,0] when it is given a list. |
Because neither a "b" nor "e" is present in the first argument, the output Association has values of 0 for those keys; otherwise, the values are just as they would be with Counts:
| In[1]:= |
| Out[1]= |
Keys not found are assumed to take on the default value of 42:
| In[2]:= |
| Out[2]= |
The association in the second argument results in missing keys being set to 0, except for key "b", which is set to 42:
| In[3]:= |
| Out[3]= |
An operator form of ItemCounts:
| In[4]:= |
| Out[4]= |
Keys in the output have the same order as keys in the second argument of the input:
| In[5]:= |
| Out[5]= |
Users can specify their own defaults for a List of values:
| In[6]:= |
| Out[6]= |
If one uses a List default, it must be the same length as the List of the keys. Otherwise, an error message is generated:
| In[7]:= |
| Out[7]= |
A very common use of this function is producing an Association with the same length and same keys when using counting items in a structure of lists:
| In[8]:= |
| Out[8]= |
Another way of going about this is to join a default Association with the Counts, but this method is less flexible:
| In[9]:= |
| Out[9]= |
One might also do it with a Merge and use the First argument for merging, but this method is similarly less flexible:
| In[10]:= |
| Out[10]= |
Duplicate keys in the second argument are eliminated:
| In[11]:= |
| Out[11]= |
An empty list in the second argument or an empty Association produces an empty Association:
| In[12]:= | ![{ResourceFunction[
"ItemCounts"][{"d", "d", "c", "d", "d", "a", "c", "c", "d"}, {}], ResourceFunction[
"ItemCounts"][{"d", "d", "c", "d", "d", "a", "c", "c", "d"}, Association[]]}](https://www.wolframcloud.com/obj/resourcesystem/images/6f0/6f0e7df7-5f7c-4aa6-82f9-5ef19898e7c0/10696a943e48bb05.png) |
| Out[12]= |
The second argument must be a List or Association:
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
Group the passengers on the Titanic over age 70 by age and count their genders:
| In[15]:= | ![Query[Select[#age > 70 &]/*GroupBy[#age &]/*KeySort, ResourceFunction["ItemCounts"][{"male", "female"}], #sex &][
ExampleData[{"Dataset", "Titanic"}]]](https://www.wolframcloud.com/obj/resourcesystem/images/6f0/6f0e7df7-5f7c-4aa6-82f9-5ef19898e7c0/0b1305f4f4ce5556.png) |
| Out[15]= | 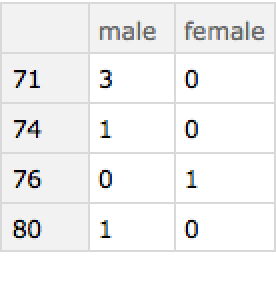 |
Find the distribution of UFO shapes by states, but limit oneself to the five most frequently seen shapes:
| In[16]:= | ![Module[{ufos = ResourceData["UFO Sightings 2015"], popularShapes},
popularShapes = Normal@Query[
DeleteMissing[#, 1] &/*Counts/*ReverseSort/*
Keys/*(Take[#, 5] &), #Shape &][ufos];
Query[GroupBy[#State &]/*KeySort, ResourceFunction["ItemCounts"][popularShapes], #Shape &][ufos]
]](https://www.wolframcloud.com/obj/resourcesystem/images/6f0/6f0e7df7-5f7c-4aa6-82f9-5ef19898e7c0/0d5e15754d465532.png) |
| Out[16]= | 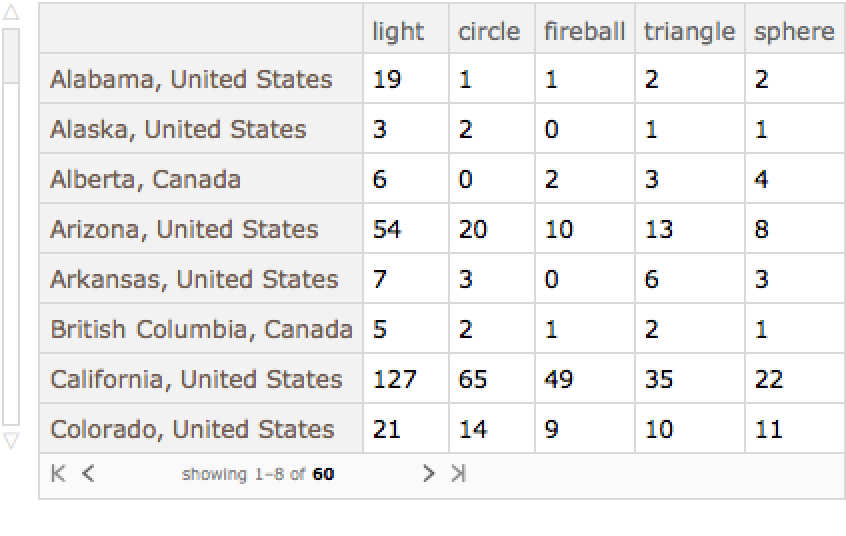 |
This work is licensed under a Creative Commons Attribution 4.0 International License