Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
List all irreducible binary compositions for a set of chosen symbols and a chosen simplification rule
ResourceFunction["IrreducibleBinaryCompositions"][rules,n,sym] returns a rules-irreducible subset of all possible binary compositions of symbols listed in sym whose proper leaf count (terminal nodes only) equals n. | |
ResourceFunction["IrreducibleBinaryCompositions"][rules,n] assumes compositions of only two formal variables, a and b. |
Generate binary compositions where a never appears as a left argument:
| In[1]:= |
| Out[1]= |
Use more than one rule to allow for quantitatively different reduction paths:
| In[2]:= |
| Out[2]= | 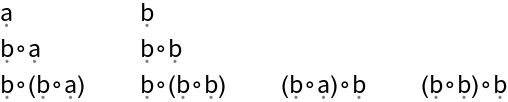 |
For some choices of rule binary compositions are totally reducible:
| In[3]:= |
| Out[3]= |
The following count of irreducible compositions is related to the super-Catalan numbers (OEIS A001003):
| In[4]:= |
| Out[4]= |
Plot irreducible expressions as trees for a choice of leaf count equals three:
| In[5]:= |
| Out[5]= |
| In[6]:= | ![Row[Map[ExpressionTree[#, ImageSize -> 100] &,
ResourceFunction[
"IrreducibleBinaryCompositions"][\[FormalA]\[SmallCircle]x_ :> x, 3] /. SmallCircle -> "\[SmallCircle]"]]](https://www.wolframcloud.com/obj/resourcesystem/images/5b7/5b7caf2c-561b-451a-a4d0-a72ee8893bc7/0858d400b69bb3b4.png) |
| Out[6]= | 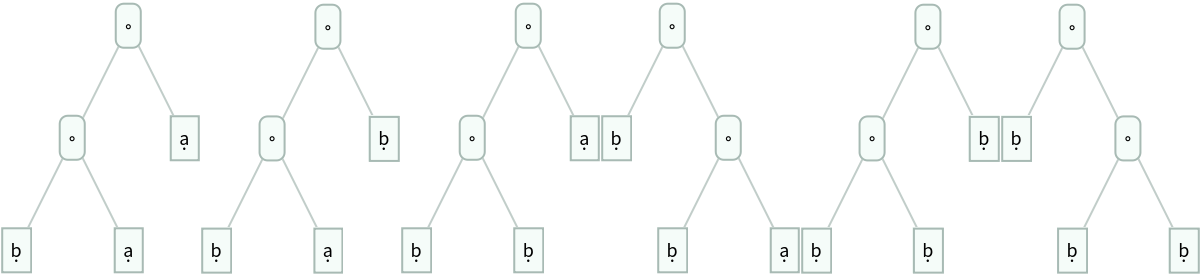 |
A sequence that does not appear in the OEIS:
| In[7]:= |
| Out[7]= |
This work is licensed under a Creative Commons Attribution 4.0 International License