Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a geometric transformation function for inversion about a point
ResourceFunction["InversionTransform"][p] gives a TransformationFunction that represents an inversion through the point p. |
Invert through the point {1,2}:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= |
Inversion transform for a symbolic point {u,v,w}:
| In[3]:= |
| Out[3]= | 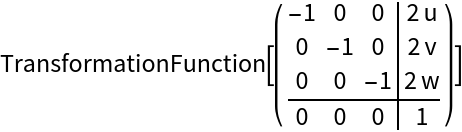 |
Apply an inversion to a 2D shape:
| In[4]:= | ![SeedRandom[497]; gr = With[{pts = RandomReal[{1, 2}, {5, 2}]},
{Polygon[pts], AbsolutePointSize[10], Opacity[1], {Magenta, Point[pts[[1]]]}, {Green, Point[pts[[2]]]}}
];](https://www.wolframcloud.com/obj/resourcesystem/images/ff8/ff878c29-e5f2-46f3-bb24-d09d40cd5eb8/63dc036c8187f8e7.png) |
| In[5]:= | ![Graphics[{{Opacity[.35], Blue, gr}, GeometricTransformation[{Opacity[.85], Red, gr}, ResourceFunction["InversionTransform"][{1, 1}]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/ff8/ff878c29-e5f2-46f3-bb24-d09d40cd5eb8/21d4bc1d202b671e.png) |
| Out[5]= | 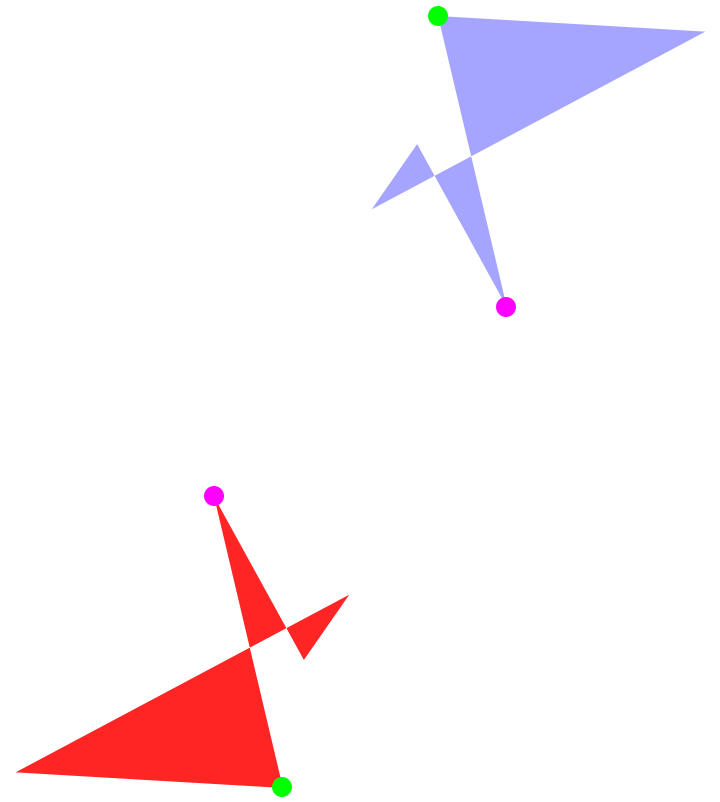 |
Apply an inversion to a 3D shape:
| In[6]:= | ![SeedRandom[47723];
gr = With[{pts = RandomReal[{1, 2}, {4, 3}]},
{Tetrahedron[pts], AbsolutePointSize[10], Opacity[1], {Magenta, Point[pts[[1]]]}, {Green, Point[pts[[2]]]}, {Orange, Point[pts[[3]]]}, {Gray, Point[pts[[4]]]}}
];](https://www.wolframcloud.com/obj/resourcesystem/images/ff8/ff878c29-e5f2-46f3-bb24-d09d40cd5eb8/1df9967d49d0c3f9.png) |
| In[7]:= | ![Graphics3D[{{Opacity[.35], Blue, gr}, GeometricTransformation[{Opacity[.35], Red, gr}, ResourceFunction["InversionTransform"][3/2 {1, 1, 1}]]}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/ff8/ff878c29-e5f2-46f3-bb24-d09d40cd5eb8/53f1a9a9ad661ef0.png) |
| Out[7]= | 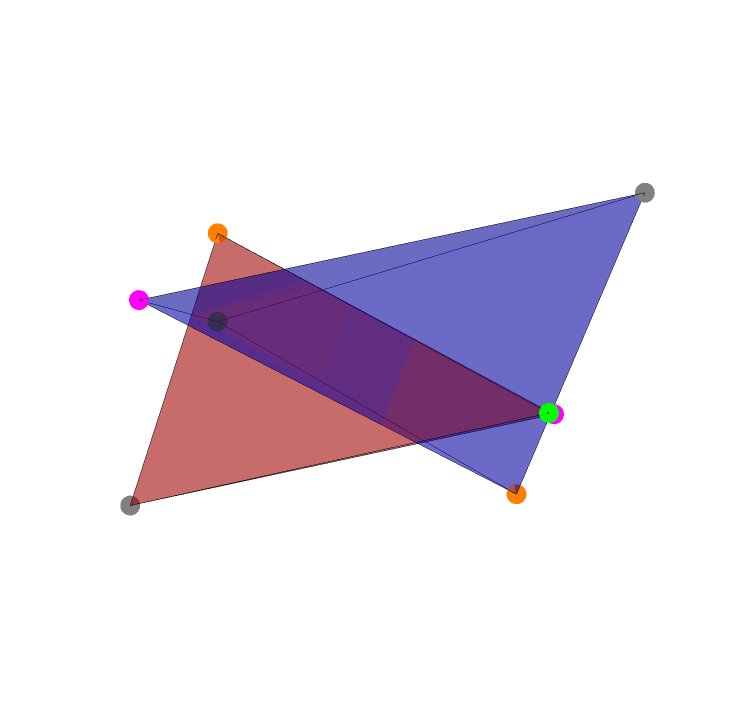 |
Invert a graphic:
| In[8]:= |
| In[9]:= | ![Show[gr, Graphics[{Point[{-1, 0}]}], gr /. L_Line :> {Red, GeometricTransformation[L, ResourceFunction[
"InversionTransform"][{-1, 0}]]}, {AspectRatio -> Automatic, Frame -> True, PlotRange -> All}]](https://www.wolframcloud.com/obj/resourcesystem/images/ff8/ff878c29-e5f2-46f3-bb24-d09d40cd5eb8/38cc688eb3825035.png) |
| Out[9]= | 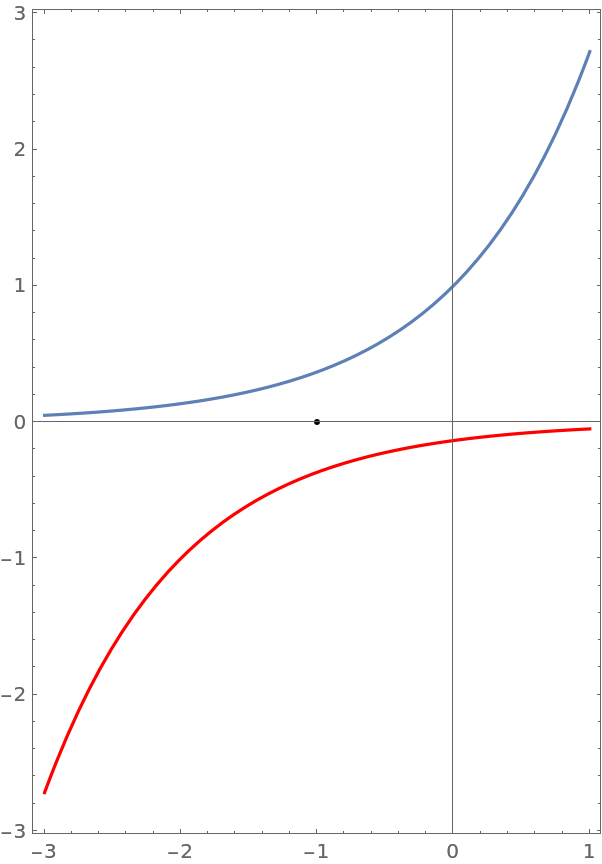 |
Invert a 2D image:
| In[10]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/cea915db-ae40-4e42-99b2-31202e6aecb7"]](https://www.wolframcloud.com/obj/resourcesystem/images/ff8/ff878c29-e5f2-46f3-bb24-d09d40cd5eb8/2f2749af78aa807e.png) |
| Out[10]= |  |
Inversion transform of a 3D image with respect to the origin:
| In[11]:= | ![ImageTransformation[\!\(\*
Graphics3DBox[
TagBox[Raster3DBox[CompressedData["
1:eJzt28GNJEt2RNEBKAkVoAqjA0UgMGuqPiJwFcCvRDX7d1SE2zP3c4DBW/Z1
W/ysyp7+z//53//+13/84x//+K+//A8AAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAABI+/c//97l
GfZey95r2XstewMAAAAAAAAAAAAAAAAAfOXfX67xd3eevvv0zrs7T3vPbp27
vCPN3mvtsvelta917xZ2zrAzAAAAAADwFH/PsIa/31nL3mvZO8POAAAAAABr
+R72He3/Pq2lt/3fX7b0PrVz6h2n9rb3r2Lv9xuf6NvtHau07nw5tbf1c3+1
Xfa+TO+7tO/cys4z2BUAAACACXwfuIbvYdfw/fca/n5nLXuvZe8MO2fYOcPO
AAAAACS1fx/b0tv+9w0tve3/HrCl962dV71D7/f3LXq/v2/R+/19i97v71v0
fn/fdlpn+h2X6X2X9p0/Te+7tO/cys4AAAAAf2b69yXt37Od0pvu172W7jXa
/37n1N72/lXs/X7jd3SvpTujrXc39gUAAIAerd+btHT7nm0Nf9/wfuMTfel3
6P3+Pq2te1Vve39bb3t/W297f1tve39b71v9l5bOS+vOn07rTL/jMr3v0r7z
p+l9l/ad29kXAAAA+rT8Pt/6vY/utXSv0f7996m97f2r2Pv9xr+y9/uNf2Xv
9xu/o3ut1u5d2BcAAAB6tH5v0tLt+9j3G5/oS79D7/f3aW3dq3rb+9t62/vb
etv723rb+9t62/vbetv723rf6r+0dF5ad/50Wmf6HZfpfZf2ndvZFwAAgDf4
ffJdbb/Pt37fo3uN9u8HT+1t73/bLn/fcFrnLu94m72/3lVad76c2tvev1pr
dzs7Z9kXAADYTfvvldN7W78/aetu/X6wrfvtv2d4q7+te1Vve39bb3t/S+db
79B7Rn9bb3t/W2/rfxdbOnd5x1Nad77o/Xv3aS2dl9adP7V0Xlp3/p2pXZdd
dm5lXwAAYFd+33lX6+/zbd3t31ed2tve/zbff3+9b7P31/s2e3+9b7P31/s2
e3+9q7TufDm1N9Xfys5Z9gUAAHbV+vtOS3fr7/Nt3a3fV7V1t37/3da9qre9
v6336f627lRve39bb3t/W297f1tve39b71P9l5bO1b3t/W29b/VfWjovrTt/
aum8tO78K9P7Lu07t7MvAACwK7/vvKv19/m27vbvq07tbe9/m++/v9632fvr
fZu9v9632fvrfZu9v95VWne+nNqb6m9l5yz7AgAAu2r9faelu/X3+Zbu9u9j
9X5/n9bWvaq3vb+t9+n+tu5Ub3t/W297f1tve39bb3t/W+9T/ZeWztW97f1t
vW/1X1o6L607fzqtM/2OT1O7PrXuuwv7AgAAu/L7zrtaf59v627/nurU3vb+
t+3yfexpnbu84232/nrfZu+v9232/npXad35cmpvqr+VnbPsCwAA7Kr1952W
7tbf59u6W7+vautu/f67rXtVb3t/W+/T/W3dqd72/rbe9v623vb+tt72/rbe
p/ovLZ2re9v723rf6r+0dF5ad/7U0nlp3flXpvdd2nduZ18AAGB3fs95V9vv
8a3fQ+heo/37wVN72/vf9vbfM7S94232/nrfZu+vd5XWnS+n9rb3r9ba3c7O
WfYFAAB20/575fTe1u9P2rpbvx9s63777xne6m/rXtXb3t/W297f0vnWO/Se
0d/W297f1tv638WWzl3e8ZTWnS96/959WkvnpXXnTy2dl9adf2dq12WXnVvZ
FwAAgCe0/H7Z+j2E7rV0r9H+feypve39q9j7/ca/svf7jX9l7/cbv6N7rdbu
XdgXAAAAerR+b9LS7fvY9xuf6Eu/Q+/392lt3at62/vbetv723rb+9t62/vb
etv723rb+9t63+q/tHReWnf+dFpn+h2X6X2X9p3b2RcAAAD6Tf/9vf37nlN6
0/2619K9Rvv336f2tvevYu/3G7+jey3dGW29u7EvAAAA9Gj93qSl2/dsa/j7
hvcbn+hLv0Pv9/dpbd2retv723rb+9t62/vbetv723rf6r+0dF5ad/50Wmf6
HZfpfZf2nT9N77u079zOvgAAAAB/j+9N1vB91Rq+h13D999r2Xste2fYOcPO
GXYGAAAAIKn9+9iW3va/b2jpbf/3Ui29b+286h16v79v0fv9fYve7+9b9H5/
36L3+/u20zrT77hM77u07/xpet+lfedWdgYAAAAAyPD96xq+917L3mvZO8PO
AAAAAABr+R72He3/nqSlt/3fS7X0tv97wFN72/tXsff7jU/07faOVVp3vpza
2/q5v9oue1+m913ad25l5xnsCgAAAAAAAAAAAAAAAM/x76TW2OXfp03v3OXf
X+7Wucs70uy91i57X1r7WvduYecMOwMAAAAAAAAAAAAAAAAAfOXfX65l77Xs
vZa917I3AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAPBT//7n
95dn/Wpnuz/r7+5s92fYey17Z9g5w84AAAAAAAAAAAAAAMCp7v47orfvrtK7
2nvG3VV619V7t/z57Xu3d7TsvWvPtL1P69r1XVO7dn3X1K5d3zW1a9d3Te1K
v+uya8/UvS/tHW17X1r+/F32Tkvvau8Zd1fpXe094wIAz0l/rp/2+Z7e2d6Z
e4r0zvbO3FOkd7Z35p4ivbO9M/cU6Z3tnbmnSO9s78w9RXpne2fuKdI72ztz
AQBapX+OOu3nq/Su9p5xn9be0bL3rj3T9j6tK/UufffuXfru3bv03bt36bt3
79J3796l7969S9+9+1OndaXfddm1Z+rel/aOtr2nSO9q7xl3V+ldT9sbABLS
n+unfb6nd7Z35p4ivbO9M/cU6Z3tnbmnSO9s78w9RXpne2fuKdI72ztzT5He
2d6Ze4r0zvbOXACAVumfo077+Sq966q92zum731aV+pd+u7du/Tduy3vaOnc
5R0tnbu8o6Vzl3e0dO7yjpbOXd7R0rnLO1o6n37HRd+9e5e+e/enTutKv+tT
e0fb3lOkd7X3jAsAPCf9uX7a53t6Z3tn7inSO9s7c0+R3tnemXuK9M72ztxT
pHe2d+aeIr2zvTP3FOmd7Z25p0jvbO/MBQBolf45atXPV+0d0/c+rSv1Ln33
bss7Wjp3eUdL51PvSHe29rb3t/W297f1tve39bb3t/W297f1tve39d7tT7+j
pXOXd7R0Pv2Oi75796dO60q/61N7R9veU6R3PW1vAEhIf66f9vme3tnemXuK
9M72ztxTpHe2d+auMvXP323vtg57r+2w99qO9r0vU//8XfdOS+9s78w9RXpn
e2fuKdI7n7Y3APC89M8b6Z+j3n7vrj1T9tZ377a8o6Vzl3e0dD71jnRna297
f1vvn/an+3TPuLp16553dc/qntbf1tve39Z7tz/9jpbOXd7R0vn0Oy767t2n
7Nozde9PLX/+LnsDwInSn+unfb6nd7Z35p4ivbO9M/cU6Z1X7d3W0br3Lj32
Xttj77U99l7bY++1PS17X9o62veeIr2zvTP3FOmd7Z25AAB/asrPHemfo956
52ldqXfpu3db3tHS+dQ70p2tve39bb1/2p/u0z3j6tate97VrVv3vLtr97T+
tt72/rbeu/3pd7R0Pv2Oi75796dO60q/61N7R9veAHCy9Of6aZ/v6Z3tnbmn
SO9s78x9W1tH69679Ezfe/euXd81tWvXd03t2vVdU7t2fdfUrmnvuuzS07L3
pa2jfe8p0jvbO3NPkd75tL0BOIvPvXdM+/kj/XPU0+/Td++2vKOl86l3pDtb
e9v723r/tD/dp3vG1a37J93prl3723rb+9t62/t/J92ne8bVrfuJ7mn9bb3t
/W29d/vT72jpfPodF3337lN27Zm696+k/lwASEh/rp/2OZve2d6Ze4r0zqv3
nvrn77L3Lj3T9969a9d3Te2a8q5T+3Z7z/S+3d4zvW+X/05O7dr1XVO7pr3r
sktPy96fpv75u+6dlt7Z3pkLADvx+feOqT+HpH+Oevpd+u7dlne0dD71jnRn
a++f9qf7dM+4unX/pDvdtWt/W297f1tve39bb3t/W297/++k+3TPuLp1P9E9
rb+t925/+h0tnU+/46Lv3v2p07rS7/qV9J8PAAnpz/XTPl/TO9s7c0+R3nnV
3m0drXvv0jN97927przr1L7d3jO9b7f3TO/b7T3T+3Z7z/S+1Hsuu3dNe9dl
l56WvS9tHe17T5He2d6ZCwA78Dn4rqk/h6R/jnr6Xfru3ZZ3tHQ+9Y50Z2vv
n/an+3TPuLt1p7t27W/rbe9v623vb+tt72/rbe9v623vb+tt7/+ddJ/uGXfX
7mn9bb13+9PvaOl8+h0XfffuT53WlX7XpykdAJCQ/lw/7XM1vbO9M/cU6Z1X
7d3W0br3Lj3T9969a8q7Tu3b7T3T+3Z7z/S+3d4zvW+390zvS73nsnvXtHdd
dulp2fvS1tG+9xTpne2duQCwA5+D75r6c0j656in36Xv3m15R0vnU+9Id7b2
/ml/uk/3jLtbd7pr1/623vb+tt72/rbe9v623vb+tt72/rbe9v7fSffpnnF3
7Z7W39Z7tz/9jpbOp99x0Xfv/tRpXel3fZrSAQAJ6c/10z5X0zvbO3NPkd55
1d5tHa1779Izfe/du6a869S+3d4zvW+390zv2+090/t2e8/0vtR7Lrt3TXvX
ZZeelr0vbR3te0+R3tnemQsAO/A5+K6pP4ekf456+l367t2Wd7R0PvWOdGdr
75/2p/t0z7i7dae7du1v623vb+tt72/rbe9v623vb+tt72/rbe//nXSf7hl3
1+5p/W29d/vT72jpfPodF3337k+d1pV+16cpHQCQkP5cP+1zNb2zvTP3FOmd
V+899c/fZe9deqbvvXvXru+a2jXlXaf27fae6X27vWd63y7/nZzateu7pnZN
e9dll56WvT9N/fN33TstvbO9MxcAduLz7x1Tfw5J/xz19Lv03bst72jpfOod
6c7W3j/tT/fpnnF16/5Jd7pr1/623vb+tt72/rbe9v623vb+30n36Z5xdet+
ontaf1vv3f70O1o6n37HRd+9+1OndaXf9SvpPx8AEtKf66d9vqZ3tnfmniK9
s70z921tHa1779Izfe/du3Z919SuXd81tWvXd03t2vVdU7umveuyS0/L3pe2
jva9p0jvbO/MPUV659P2BuAsPvfeMe3nj/TPUU+/T9+92/KOls6n3pHubO1t
72/r/dP+dJ/uGVe37p90p7t27W/rbe9v623v/510n+4ZV7fuJ7qn9bf1tve3
9d7tT7+jpfPpd1z03btP2bVn6t6/kvpzASAh/bl+2udsemd7Z+4p0jvbO3NP
kd45/fvw1I7WvXfpsffaHnuv7bH32h57r+1p2fvS1tG+9xTpne2duadI72zv
zAUA+FNTfu5I/xz11jtP60q9S9+92/KOls6n3pHubO1t72/r/dP+dJ/uGVe3
bt3zrm7duufdXbun9bf1tve39d7tT7+jpfPpd1z03bs/dVpX+l2f2jva9gaA
k6U/10/7fE/vbO/MPUV6Z3tn7inSO9s7c1eZ+ufvtndbh73Xdth7bUf73pep
f/6ue6eld7Z35p4ivbO9M/cU6Z1P2xsAeF765430z1Fvv3fXnil767t3W97R
0rnLO1o6n3pHurO1t72/rfdP+9N9umdc3bp1z7u6Z3VP62/rbe9v673bn35H
S+cu72jpfPodF3337lN27Zm696eWP3+XvQHgROnP9dM+39M72ztzT5He2d6Z
e4r0zvbO3FOkd7Z35p4ivbO9M/cU6Z3tnbmnSO9s78w9RXpne2cuAECr9M9R
q36+au+YvvdpXal36bt3W97R0rnLO1o6n3pHurO1t72/rbe9v623vb+tt72/
rbe9v623vb+t925/+h0tnbu8o6Xz6Xdc9N27P3VaV/pdn9o72vaeIr3raXsD
QEL6c/20z/f0zvbO3FOkd7Z35p4ivbO9M/cU6Z3tnbmnSO9s78w9RXpne2fu
KdI72ztzT5He2d6ZCwDQKv1z1Gk/X6V3XbV3e8f0vU/rSr1L3717l757t+Ud
LZ27vKOlc5d3tHTu8o6Wzl3e0dK5yztaOnd5R0vn0++46Lt379J37/7UaV3p
d31q72jbe4r0rvaecQGA56Q/10/7fE/vbO/MPUV6Z3tn7inSO9s7c0+R3tne
mXuK9M72ztxTpHe2d+aeIr2zvTP3FOmd7Z25AACt0j9HnfbzVXpXe8+4T2vv
aNl7155pe5/WlXqXvnv3Ln337l367t279N27d+m7d+/Sd+/epe/e/anTutLv
uuzaM3XvS3tH295TpHe194y7q/Sup+0NAAAAAAAAAAAAE6T/f4Kn/f8H07va
e8bdVXrX1Xu3/Pnte7d3tOy9a8+0vU/r2vVdU7t2fdfUrl3fNbVr13dN7Uq/
67Jrz9S9L+0dbXtfWv78XfZOS+9q7xl3V+ld7T3jAgAAAAAAAAAAAAAA6/n/
+a/h31es4d+1rGXvteydYecMOwMAAAAAAAAAAAAAAAAAAAAAAADw//s/Vaix
FA==
"], {{0, 46, 46}, {46, 0, 0}}, {0., 1.},
ColorFunction->"GrayLevelDefaultColorFunction",
Method->{"FastRendering" -> True}],
BoxForm`ImageTag[
"Real", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
AxesStyle->{},
Background->None,
BaseStyle->"Image3DGraphics3D",
BoxRatios->Automatic,
Boxed->False,
ImageSizeRaw->46,
PlotRange->{{0, 46}, {0, 46}, {0, 46}}]\), ResourceFunction["InversionTransform"][{0, 0, 0}], DataRange -> {{-.5, .5}, {-.5, .5}, {-.5, .5}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ff8/ff878c29-e5f2-46f3-bb24-d09d40cd5eb8/45830838f2d4a5b9.png) |
| Out[11]= |  |
Invert the geometry and stereochemistry of a chiral molecule:
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
Show the two enantiomers:
| In[14]:= |
| Out[14]= | 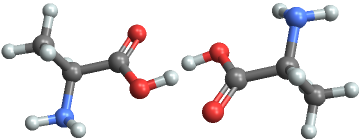 |
| In[15]:= |
| Out[15]= |
The inversion transformation is an isometric transform—that is, it preserves distances:
| In[16]:= |
| In[17]:= |
| In[18]:= |
| Out[18]= |
The inversion transformation is its own inverse:
| In[19]:= |
| In[20]:= |
| Out[20]= |
The determinant of the transformation matrix is –1 for odd-order dimensions and +1 for even-order dimensions:
| In[21]:= |
| In[22]:= |
| Out[22]= |
This work is licensed under a Creative Commons Attribution 4.0 International License