Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the inversion surface
ResourceFunction["InversionSurface"][ρ,s,t] computes the inversion of a surface s with respect to a sphere of radius ρ and parameters u, v. | |
ResourceFunction["InversionSurface"][q,ρ,s,t] computes the inversion with respect to a sphere displaced to a point q. |
Define a torus:
| In[1]:= |
| Out[1]= |
The inverse surface of a torus is a Dupin cyclide:
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= |
Visualize them:
| In[4]:= | ![ParametricPlot3D[
Evaluate[{Entity["Surface", "Torus"]["ParametricEquations"][3, 2][u, v], ResourceFunction["InversionSurface"][1.5, Entity["Surface", "Torus"]["ParametricEquations"][3, 2][u, v], {u,
v}]}], {u, 0, 2 \[Pi]}, {v, 0, 2 \[Pi]}, PlotStyle -> Opacity[.5], PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/9ca/9caee9ff-c5a0-4351-801d-75d12ce4ac4c/1329894ec00c8054.png) |
| Out[4]= | 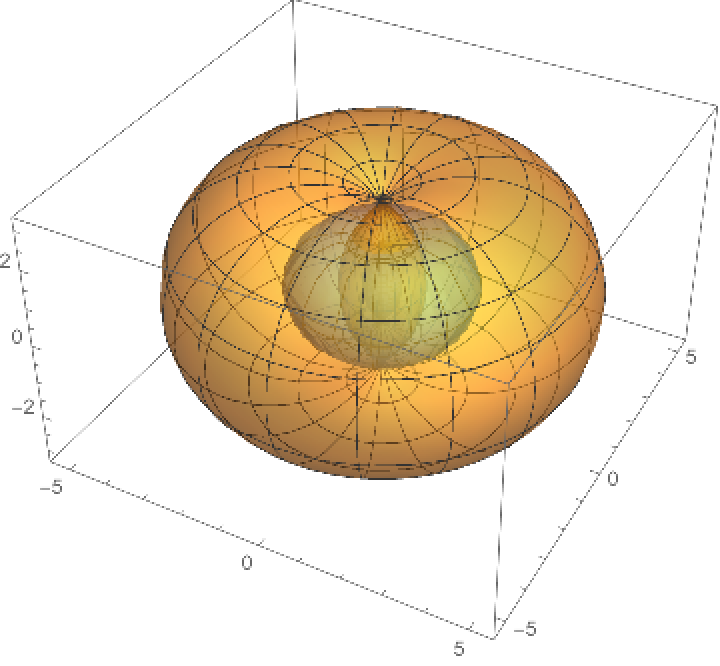 |
Define a helicoid:
| In[5]:= |
| Out[5]= |
The inverse surface of a helicoid:
| In[6]:= | ![ResourceFunction["InversionSurface"][1.5, Entity["Surface", "Helicoid"]["ParametricEquations"][1][u, v], {u, v}] // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/9ca/9caee9ff-c5a0-4351-801d-75d12ce4ac4c/1b9ba2bd649366c6.png) |
| Out[6]= |
A plot, including the inversion sphere:
| In[7]:= | ![Show[ParametricPlot3D[
Evaluate[Entity["Surface", "Helicoid"]["ParametricEquations"][.5][u,
v]], {u, 0, 2}, {v, -\[Pi], \[Pi]}, PlotPoints -> 50, PlotStyle -> Opacity[.5], MaxRecursion -> 3, PlotRange -> {{-2, 2}, {-2, 2}, {-1, 1}}], ParametricPlot3D[
Evaluate[FullSimplify[
ResourceFunction["InversionSurface"][ 1, Entity["Surface", "Helicoid"]["ParametricEquations"][1][u, v], {u, v}]]], {u, - 2 \[Pi], 2 \[Pi]}, {v, -2 \[Pi], 2 \[Pi]}, ExclusionsStyle -> None, PlotStyle -> {Opacity[.5], Blue}, PlotPoints -> 50, MaxRecursion -> 3, PlotRange -> 2.5], Graphics3D[{Opacity[.5], Sphere[]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/9ca/9caee9ff-c5a0-4351-801d-75d12ce4ac4c/132aecc0311f4ad9.png) |
| Out[7]= | 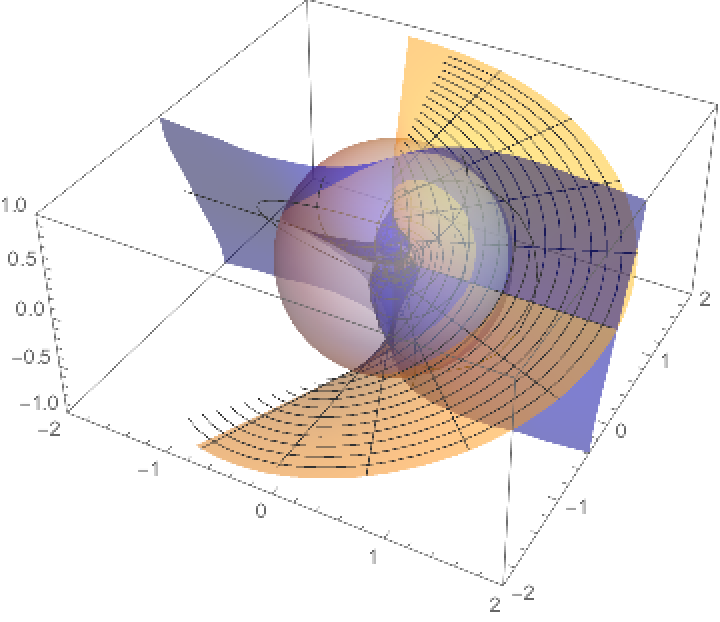 |
Zoom in near the origin:
| In[8]:= | ![Show[ParametricPlot3D[
Evaluate[{FullSimplify[
ResourceFunction["InversionSurface"][ 1, Entity["Surface", "Helicoid"]["ParametricEquations"][1][u, v], {u, v}]]}], {u, - 2 \[Pi], 2 \[Pi]}, {v, -2 \[Pi], 2 \[Pi]}, ExclusionsStyle -> None, PlotStyle -> Opacity[.5], PlotPoints -> 50, MaxRecursion -> 3, PlotRange -> .5]]](https://www.wolframcloud.com/obj/resourcesystem/images/9ca/9caee9ff-c5a0-4351-801d-75d12ce4ac4c/3a14da952c7cc8e5.png) |
| Out[8]= | 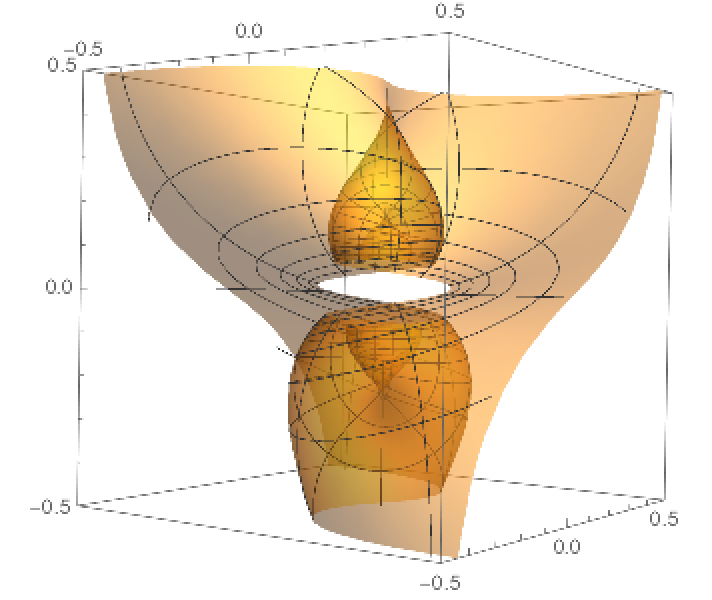 |
The inversion displaced to a point q:
| In[9]:= | ![Show[ParametricPlot3D[
Evaluate[FullSimplify[
ResourceFunction["InversionSurface"][ .2 {1, 1, 1}, 1, Entity["Surface", "Helicoid"]["ParametricEquations"][1][u, v], {u, v}]]], {u, - 2 \[Pi], 2 \[Pi]}, {v, -2 \[Pi], 2 \[Pi]}, ExclusionsStyle -> None, PlotStyle -> {Opacity[.5], Blue}, PlotPoints -> 50, MaxRecursion -> 3, PlotRange -> 1.]]](https://www.wolframcloud.com/obj/resourcesystem/images/9ca/9caee9ff-c5a0-4351-801d-75d12ce4ac4c/4c3322ea598498f0.png) |
| Out[9]= | 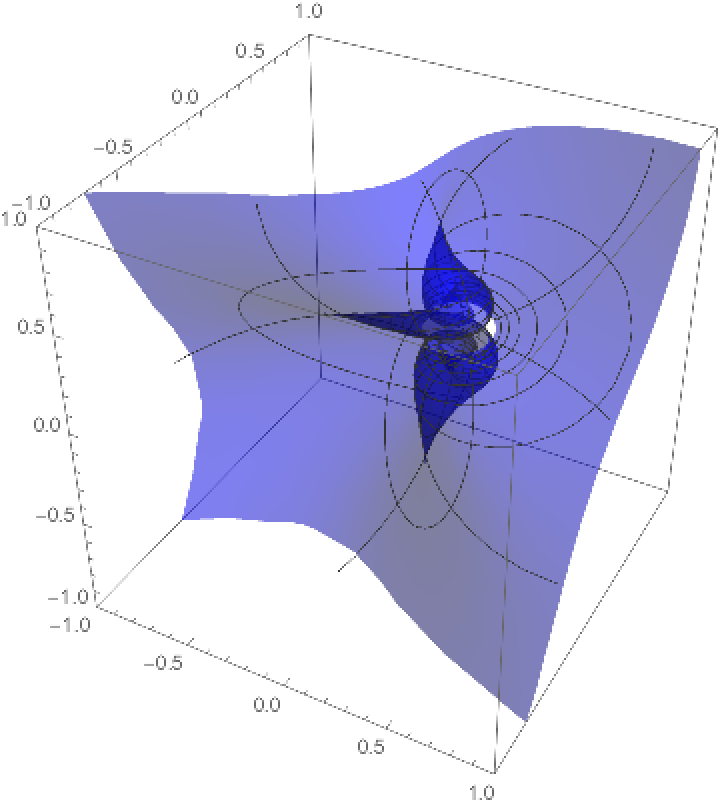 |
This work is licensed under a Creative Commons Attribution 4.0 International License