Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 InversionCount

Source Notebook

Count the number of pairs of out-of-order elements in a permutation

Contributed by: Wolfram Staff (original content by Sriram V. Pemmaraju and Steven S. Skiena)

ResourceFunction["InversionCount"][p]

counts the number of inversions in permutation p.

Examples

Basic Examples (1) 

InversionCount gives the number of pairs of elements that must be reversed to bring the permutation to canonical order:

In[1]:=
ResourceFunction["InversionCount"][{1, 3, 2, 5, 4}]
Out[1]=
In[2]:=
ResourceFunction["InversionCount"][{1, 2, 3, 4, 5}]
Out[2]=
In[3]:=
ResourceFunction["InversionCount"][Range[5]]
Out[3]=

Properties and Relations (7) 

The number of inversions in a permutation of size n ranges from 0 to :

In[4]:=
n = 5;
In[5]:=
Union[ResourceFunction["InversionCount"] /@ Permutations[Range[n]]]
Out[5]=
In[6]:=
{Max[%], Binomial[n, 2]}
Out[6]=

The largest inversion count comes from the reverse of the identity permutation:

In[7]:=
ResourceFunction["InversionCount"][Reverse[Range[n]]]
Out[7]=

There are an average of n(n-l)/4 inversions per permutation:

In[8]:=
n = 5;
In[9]:=
data = Table[ ResourceFunction["InversionCount"][ RandomPermutation[n] // PermutationList], {5000}];
In[10]:=
{m = Mean[data] // N, Binomial[n, 2]/2}
Out[10]=
In[11]:=
highlightbar[{{x0_, x1_}, {y0_, y1_}}, d_, meta___] := {If[x0 <= First[meta] < x1, Red, {}], Rectangle[{x0, y0}, {x1, y1}]}
In[12]:=
Histogram[data -> m, ChartElementFunction -> highlightbar]
Out[12]=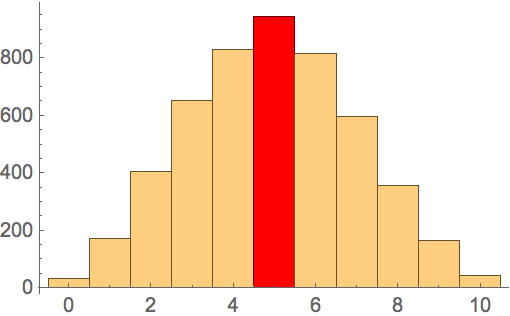

The number of inversions in a permutation is equal to that of its inverse:

In[13]:=
p = RandomPermutation[10] // PermutationList
Out[13]=
In[14]:=
{ResourceFunction["InversionCount"][p], ResourceFunction["InversionCount"][InversePermutation[p]]}
Out[14]=

The number of permutations of length n with major index k and inversion count i is the same as the number of permutations of length n with major index i and inversion count k:

In[15]:=
n = 7; k = 10; i = 4;
In[16]:=
p = Permutations[Range[n]];
In[17]:=
Length[Select[ p, (ResourceFunction["PermutationMajorIndex"][#] == k && ResourceFunction["InversionCount"][#] == i) &]] === Length[Select[ p, (ResourceFunction["PermutationMajorIndex"][#] == i && ResourceFunction["InversionCount"][#] == k) &]]
Out[17]=

The number of inversions is a sum of elements of the inversion vector:

In[18]:=
p = RandomPermutation[5] // PermutationList
Out[18]=
In[19]:=
ResourceFunction["ToInversionVector"][p]
Out[19]=
In[20]:=
Total[%]
Out[20]=
In[21]:=
ResourceFunction["InversionCount"][p]
Out[21]=

The number of inversions in a permutation is equal to the number of edges in its permutation graph:

In[22]:=
p = RandomPermutation[15] // PermutationList
Out[22]=
In[23]:=
{ResourceFunction["InversionCount"][p], EdgeCount[ResourceFunction["PermutationGraph"][p]]}
Out[23]=

The number of n permutations with k inversions is given by the resource function PermutationCountByInversions:

In[24]:=
n = 4; k = 3;
In[25]:=
Select[Permutations[ Range[n]], (ResourceFunction["InversionCount"][#] == k) &]
Out[25]=
In[26]:=
Length[%]
Out[26]=
In[27]:=
ResourceFunction["PermutationCountByInversions"][n, k]
Out[27]=

Version History

  • 1.0.0 – 06 July 2020

Related Resources

License Information