Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Convert a permutation into one whose number of excedances equals the number of descents in the original
ResourceFunction["InverseFoataTransform"][perm] generates a permutation whose number of excedances matches the number of descents in the original permutation perm. |
Generate the corresponding permutation given a permutation ![]() displayed in two line notation:
displayed in two line notation:
| In[1]:= |
| Out[1]= |
The InverseFoataTransform is indeed the inverse of ResourceFunction["FoataTransform"]:
| In[2]:= |
| Out[2]= |
The inverse transform converts the result above back into the input:
| In[3]:= |
| Out[3]= |
InverseFoataTransform produces a permutation Φ-1(p) whose number of excedances matches the number of descents in the original permutation p. Generate a random permutation:
| In[4]:= |
| Out[5]= |
Apply InverseFoataTransform onto the given permutation:
| In[6]:= |
| Out[6]= |
Verify the equidistribution property between two permutations, DES(w)=EXC(Φ-1(w)):
| In[7]:= |
| In[8]:= |
Show the indices of descent from the original permutation and the indices of excedance of the transformed permutation:
| In[9]:= |
| Out[9]= |
The number of elements are the same in each list:
| In[10]:= |
| Out[10]= |
Find the correspondence that links the original permutation and the one after the application of the inverse transform:
| In[11]:= | ![circleLayout[n_] := Table[{Cos[2. \[Pi]/n i], Sin[2. \[Pi]/n i]}, {i, 0, n - 1}];
n = 20;
r = Range[n];
SeedRandom[17];
p1 = Permute[r, RandomPermutation[n]];
p2 = ResourceFunction["InverseFoataTransform"][p1];
cyc2 = FindPermutation[p1, p2];
Graph[Thread[r -> PermutationList[cyc2, n]],
VertexLabels -> Placed[Automatic, Center],
VertexCoordinates -> Thread[r -> circleLayout[n]],
VertexSize -> .5, ImageSize -> 360
]](https://www.wolframcloud.com/obj/resourcesystem/images/89d/89de10d7-f275-49ee-a3aa-cdb0f322c153/3c9a59a9881a08a3.png) |
| Out[12]= | 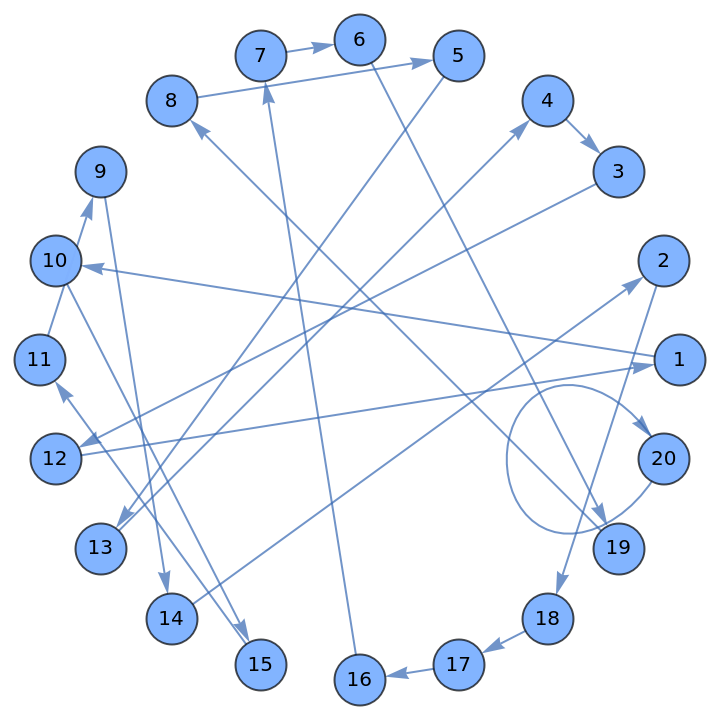 |
This work is licensed under a Creative Commons Attribution 4.0 International License