Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 InverseFibonacci

Source Notebook

Compute the inverse Fibonacci function

Contributed by: Carl Woll

ResourceFunction["InverseFibonacci"][s]

gives the inverse Fibonacci function obtained as the solution for z in s=Fibonacci[z].

Details and Options

Mathematical function, suitable for both symbolic and numerical manipulation.
Explicit numerical values are given only for real values of s≥1.
For certain special arguments, ResourceFunction["InverseFibonacci"] automatically evaluates to exact values.
ResourceFunction["InverseFibonacci"] can be evaluated to arbitrary numerical precision.
ResourceFunction["InverseFibonacci"] automatically threads over lists.

Examples

Basic Examples (2) 

Evaluate InverseFibonacci numerically:

In[1]:=
ResourceFunction["InverseFibonacci"][252.1]
Out[1]=

Plot InverseFibonacci over a subset of the reals:

In[2]:=
Plot[ResourceFunction["InverseFibonacci"][z], {z, 1, 200}]
Out[2]=

Scope (6) 

Numerical Evaluation (4) 

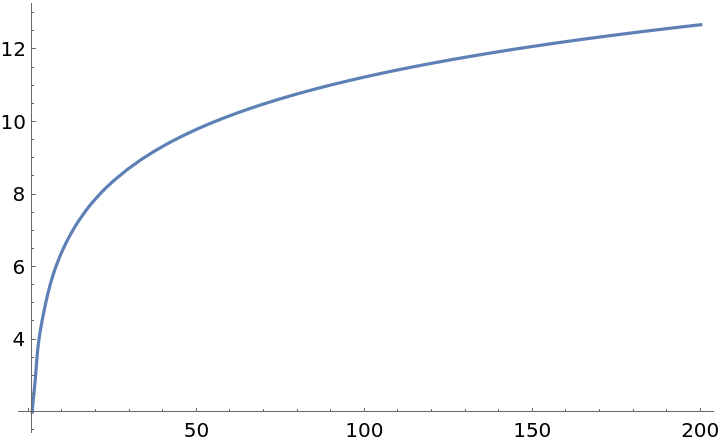Evaluate numerically to high precision:

In[3]:=
N[ResourceFunction["InverseFibonacci"][222 + 1/4], 50]
Out[3]=

The precision of the output tracks the precision of the input:

In[4]:=
ResourceFunction["InverseFibonacci"][222.25`30]
Out[4]=

Evaluate InverseFibonacci efficiently at high precision:

In[5]:=
ResourceFunction["InverseFibonacci"][222.25`500] // Timing
Out[5]=

InverseFibonacci threads elementwise over lists and arrays:

In[6]:=
ResourceFunction["InverseFibonacci"][1000/{2., 3., 4., 5.}]
Out[6]=

Specific Values (1) 

Fibonacci integer inputs return integer results:

In[7]:=
ResourceFunction["InverseFibonacci"][Fibonacci[100]]
Out[7]=

Differentiation (1) 

InverseFibonacci can be differentiated:

In[8]:=
ResourceFunction["InverseFibonacci"]'[x]
Out[8]=

Publisher

Carl Woll

Version History

  • 1.0.0 – 18 October 2019

Author Notes

I modified the error estimate (which was purely heuristic before). I don’t know where this goes, but here’s an idea of how the code works, and how I obtained the new error estimate. First FunctionExpand Fibonacci:

In[1]:=
FunctionExpand[Fibonacci[n]]

Then, an approximation to the inverse for large n:

In[2]:=
approx = n /. First@ Solve[ReplaceAll[_Cos -> 1]@FunctionExpand[Fibonacci[n]] == z, n, Reals]

Series expand:

In[3]:=
s = Series[approx, {z, Infinity, 2}]

So, the leading order approximation is the first term, which can be rewritten as Log[GoldenRatio,Sqrt[5]z]. The error (which should be larger than the actual error because Abs[Cos[x]]<1) is:

In[4]:=
SeriesCoefficient[ s/SeriesCoefficient[s, {z, Infinity, 0}], {z, Infinity, 2}]

So, an approximation to the relative error is , implying that the precision of the answer is less than . Now, Root only needs an approximate root sufficiently close so that there is only 1 actual root in the vicinity of the approximate root. Hence, we can construct a Root object by specifying the needed relation, and using an approximate root. For large enough inputs, the above approximation is sufficient to enable Root to work.

License Information