Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 IntrinsicCurvedManifoldToGraph

Source Notebook

Produce random spatial graphs by sprinkling points into a Riemannian manifold with a specified intrinsic algebraic curvature function

Contributed by: Jonathan Gorard

ResourceFunction["IntrinsicCurvedManifoldToGraph"][func,{x,xmin,xmax},n]

produces a random sprinkling of n points into a 1-dimensional Riemannian manifold with intrinsic algebraic curvature given by func as a function of x, assuming a discreteness scale of 1.

ResourceFunction["IntrinsicCurvedManifoldToGraph"][func,{x,xmin,xmax},disc,n]

produces a random sprinkling of n points with discreteness scale disc into a 1-dimensional Riemannian manifold with intrinsic algebraic curvature given by func as a function of x.

ResourceFunction["IntrinsicCurvedManifoldToGraph"][func,{x,…},{y,…},…,n]

produces a random sprinkling of n points into a higher-dimensional Riemannian manifold with multi-variable intrinsic algebraic curvature function func (in variables x,y,…, etc.), assuming a discreteness scale of 1.

ResourceFunction["IntrinsicCurvedManifoldToGraph"][func,{x,…},{y,…},…,disc,n]

uses discreteness scale disc.

ResourceFunction["IntrinsicCurvedManifoldToGraph"][…,"prop"]

gives the property "prop" for the Riemannian manifold sprinkling with the specified intrinsic algebraic curvature function.

Details and Options

When no "prop" argument is given, ResourceFunction["IntrinsicCurvedManifoldToGraph"] returns a ManifoldGraph object by default.
By default, the discreteness scale is assumed to be equal to 1.
Unlike the resource function FlatManifoldToGraph, sprinklings can only be performed in 1-, 2- and 3-dimensional manifolds using ResourceFunction["IntrinsicCurvedManifoldToGraph"].
Note that, in the multi-variable case, only algebraic curvature functions are supported.
Sprinklings are performed using a Poisson point process, with the expected number of sprinkled points being proportional to the Riemannian volume measure.
Spatial edges are added in accordance with both the Riemannian metric and the specified discreteness scale, so as to guarantee approximate isometry between the spatial graph and the underlying manifold.
ResourceFunction["IntrinsicCurvedManifoldToGraph"] uses a similar argument specification to ProbabilityDistribution.
In ResourceFunction["IntrinsicCurvedManifoldToGraph"][…,"prop"], the following properties can be requested. These are the same as the properties supported by ManifoldGraph[…]["prop"]:
"SpatialGraph"spatial graph with vertex coordinates given by the underlying manifold coordinates
"Points"plot of the sprinkled points only (without spatial edges)
"PointsList"list of the manifold coordinates of all sprinkled points
"DiscretenessScale"discreteness scale of the sprinkling
"PointsCount"number of sprinkled points
"Dimensions"number of dimensions in the continuum manifold approximation
"EdgeCount"total number of spatial edges
"PureSpatialGraph"spatial graph with vertex coordinate information removed
"Properties"list of properties
The discreteness scale determines at what distance (with respect to the Riemannian metric) a pair of points should be regarded as adjacent.

Examples

Basic Examples (4) 

A 2-variable algebraic curvature function:

In[1]:=
Plot3D[x^4 + y^4, {x, -1, 1}, {y, -1, 1}]
Out[1]=

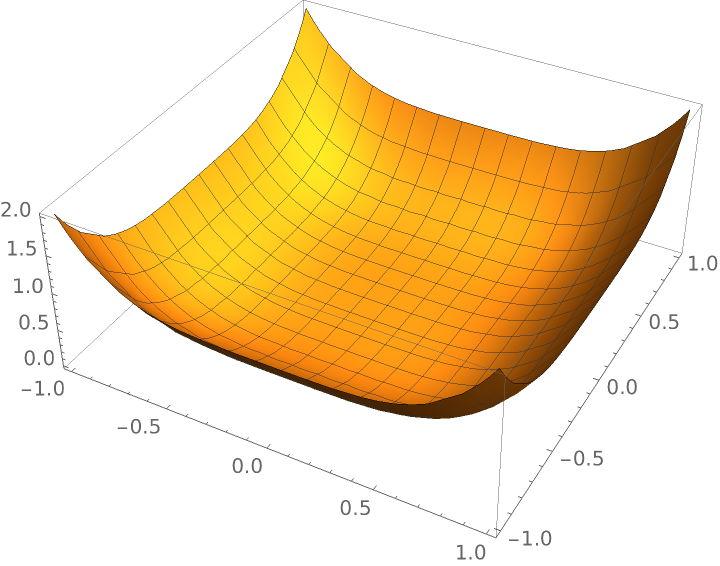
Produce a random sprinkling of 100 points into a 2-dimensional Riemannian manifold with the specified intrinsic curvature function, with discreteness scale 0.5:

In[2]:=
manifold = ResourceFunction["IntrinsicCurvedManifoldToGraph"][ x^4 + y^4, {x, -1, 1}, {y, -1, 1}, 0.5, 100]
Out[2]=

Show the spatial graph:

In[3]:=
manifold["SpatialGraph"]
Out[3]=

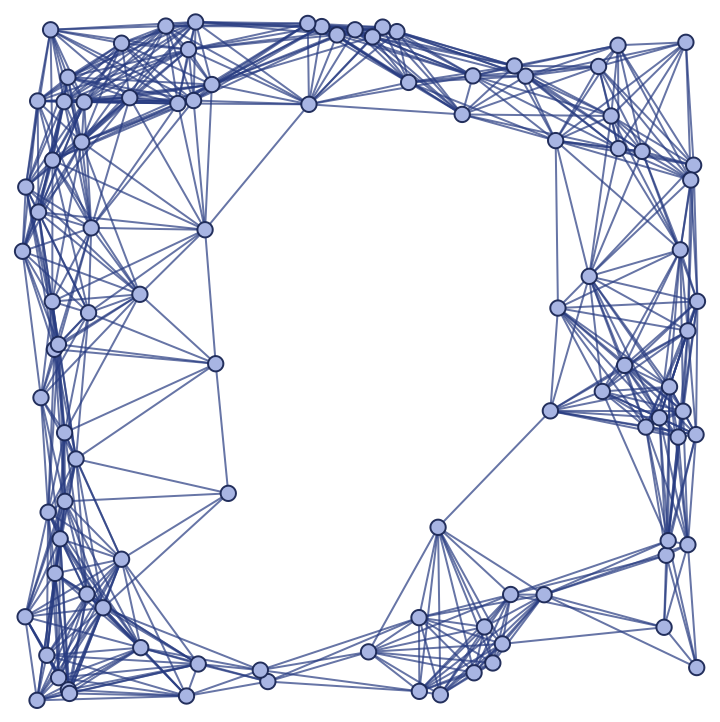
Show the pure spatial graph (with vertex coordinate information removed):

In[4]:=
manifold["PureSpatialGraph"]
Out[4]=

A slightly more complicated 2-variable algebraic curvature function:

In[5]:=
Plot3D[x^2 + 2 y^2 + 3 x^3 + 4 y^4 + 5 x^5 + 6 y^6, {x, -1, 1}, {y, -1, 1}]
Out[5]=

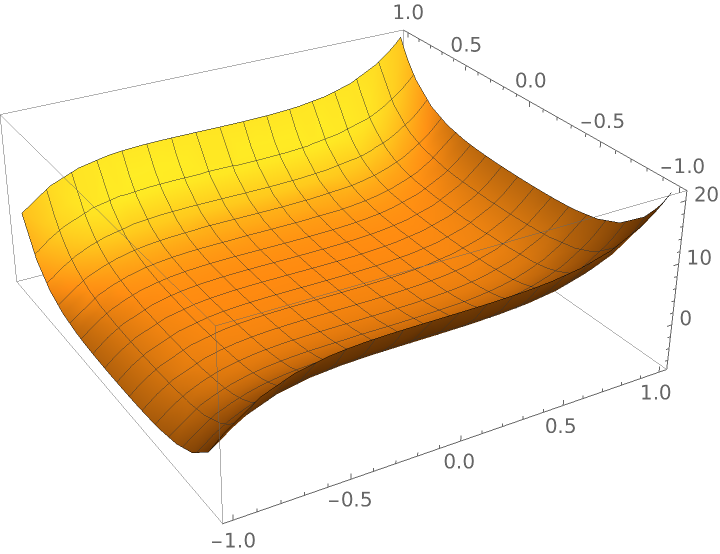
Produce a random sprinkling of 200 points into a 3-dimensional Riemannian manifold with the specified intrinsic curvature function, with discreteness scale 0.3:

In[6]:=
manifold = ResourceFunction["IntrinsicCurvedManifoldToGraph"][ x^2 + 2 y^2 + 3 x^3 + 4 y^4 + 5 x^5 + 6 y^6, {x, -1, 1}, {y, -1, 1}, 0.3, 200]
Out[6]=

Show the spatial graph:

In[7]:=
manifold["SpatialGraph"]
Out[7]=

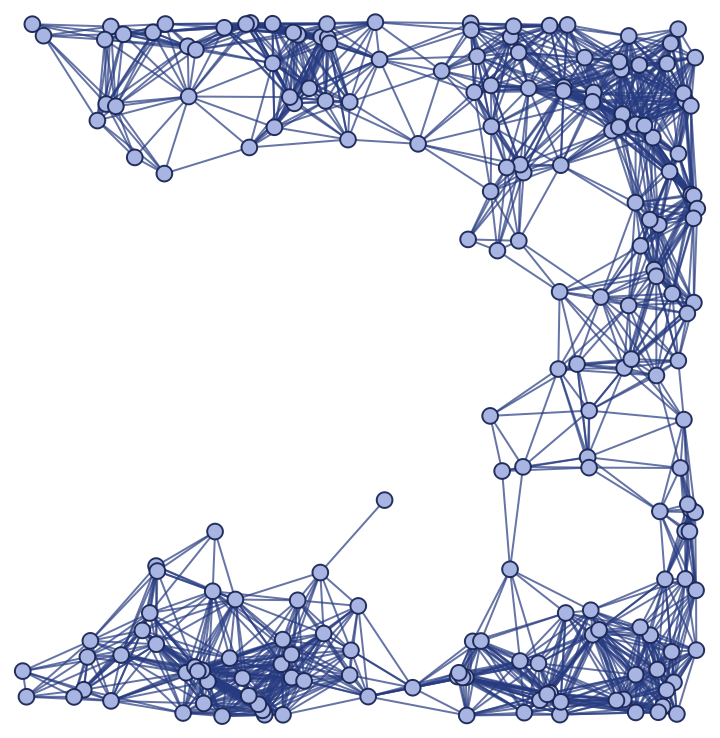
Show the pure spatial graph (with vertex coordinate information removed):

In[8]:=
manifold["PureSpatialGraph"]
Out[8]=

Plot the positions of the sprinkled points only (without spatial edges):

In[9]:=
manifold["Points"]
Out[9]=

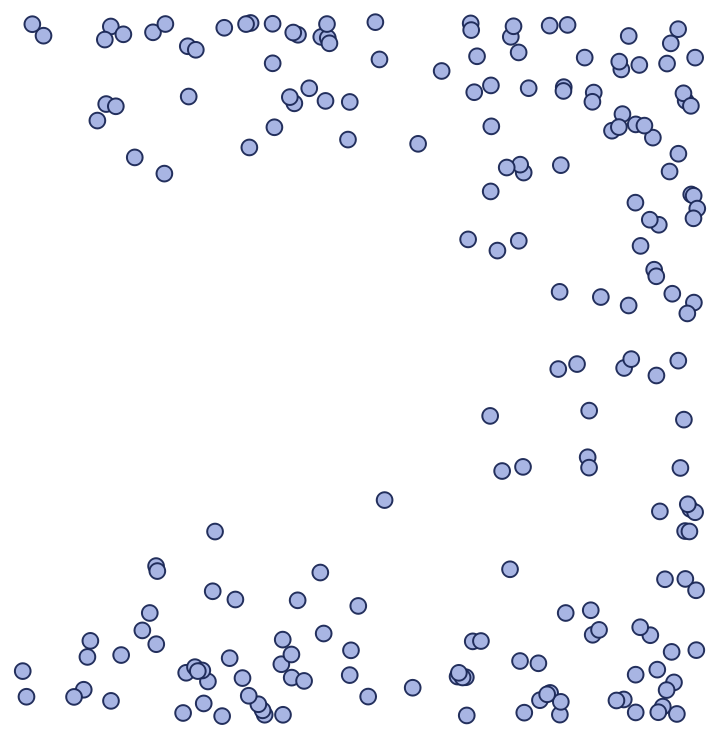
A 3-variable algebraic curvature function:

In[10]:=
ContourPlot3D[x^3 + y^2 - z, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}]
Out[10]=

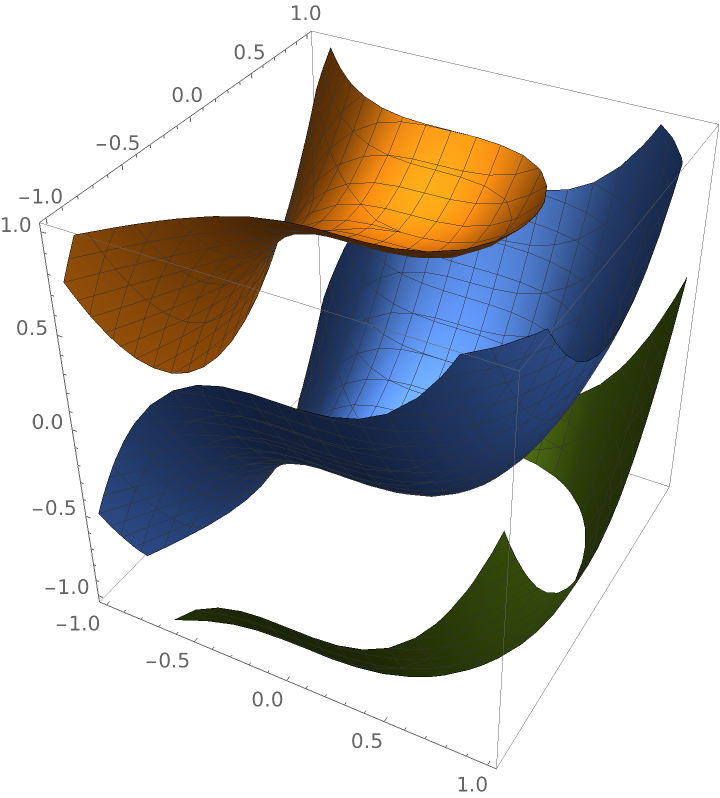
Produce a random sprinkling of 300 points into a 3-dimensional Riemannian manifold with the specified intrinsic curvature function, with discreteness scale 0.4:

In[11]:=
manifold = ResourceFunction["IntrinsicCurvedManifoldToGraph"][ x^3 + y^2 - z, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, 0.4, 300]
Out[11]=

Plot the positions of the sprinkled points only (without spatial edges):

In[12]:=
manifold["Points"]
Out[12]=

Show the spatial graph:

In[13]:=
manifold["SpatialGraph"]
Out[13]=

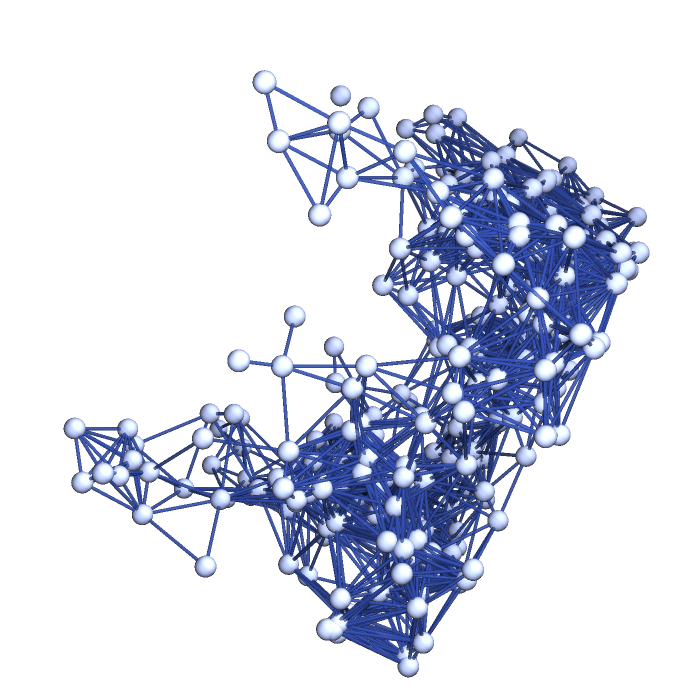
Show the pure spatial graph (with vertex coordinate information removed):

In[14]:=
manifold["PureSpatialGraph"]
Out[14]=

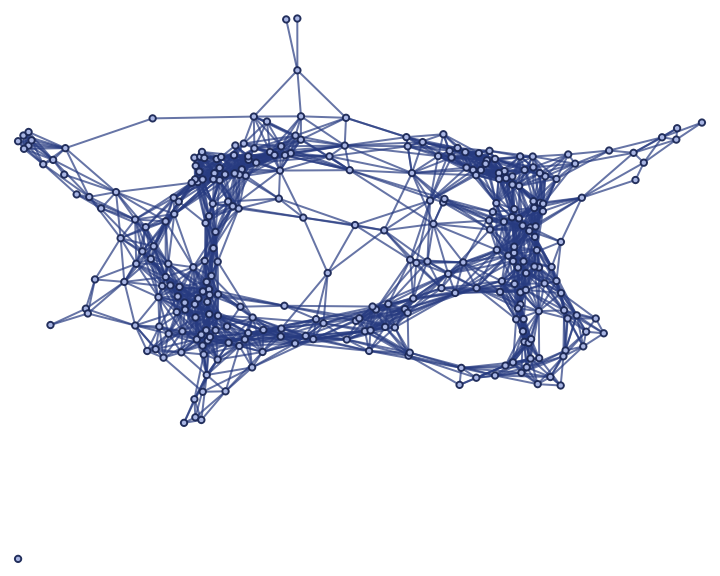
By default, the discreteness scale is assumed to be equal to 1:

In[15]:=
manifold = ResourceFunction["IntrinsicCurvedManifoldToGraph"][ x^4 + y^4, {x, -1, 1}, {y, -1, 1}, 40]
Out[15]=

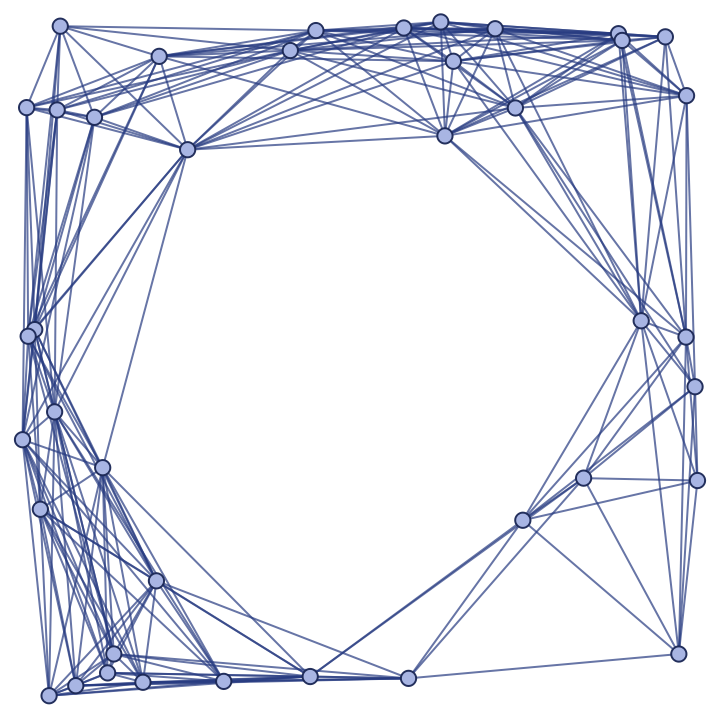
Show the spatial graph:

In[16]:=
manifold["SpatialGraph"]
Out[16]=

Scope (5) 

Sprinklings can be produced in 1-dimensional Riemannian manifolds:

In[17]:=
manifold = ResourceFunction["IntrinsicCurvedManifoldToGraph"][x^2, {x, -1, 1}, 20]
Out[17]=

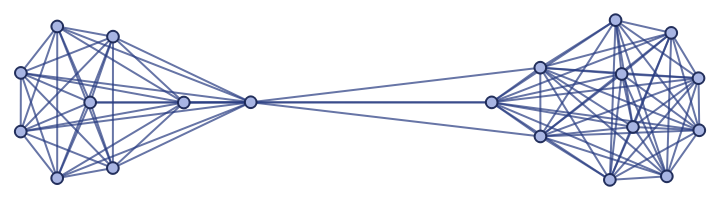
Show the spatial graph:

In[18]:=
manifold["SpatialGraph"]
Out[18]=

Produce a sprinkling in a 2-dimensional Riemannian manifold:

In[19]:=
manifold2 = ResourceFunction["IntrinsicCurvedManifoldToGraph"][ x^4 + y^4, {x, -1, 1}, {y, -1, 1}, 0.3, 200]
Out[19]=

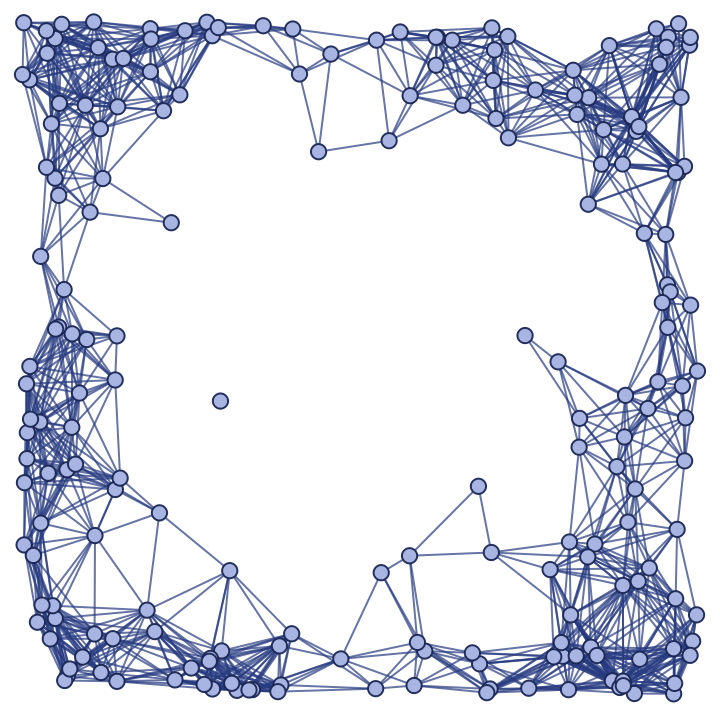
Show the spatial graph:

In[20]:=
manifold2["SpatialGraph"]
Out[20]=

Produce a sprinkling in a 3-dimensional Riemannian manifold:

In[21]:=
manifold3 = ResourceFunction["IntrinsicCurvedManifoldToGraph"][ x^3 + y^2 - z, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, 0.4, 200]
Out[21]=

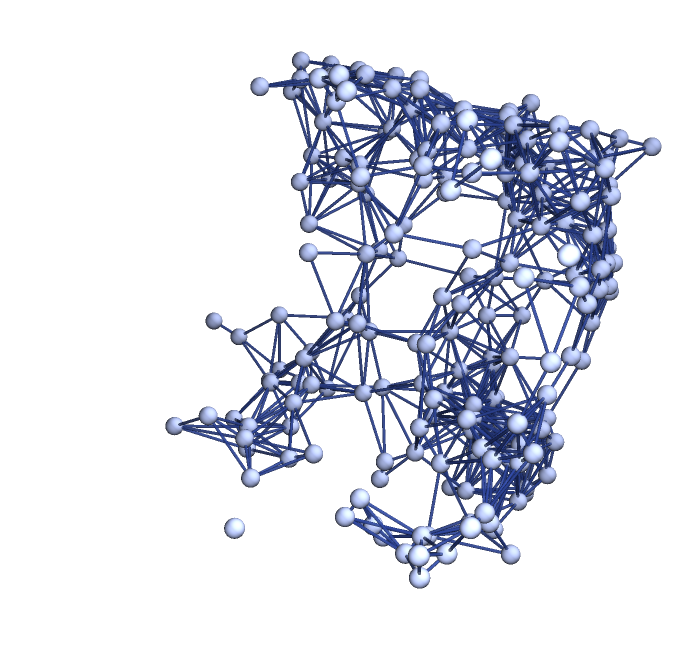
Show the spatial graph. Note that, unlike the resource function FlatManifoldToGraph, IntrinsicCurvedManifoldToGraph does not support higher-dimensional sprinklings:

In[22]:=
manifold3["SpatialGraph"]
Out[22]=

Properties can be requested directly from IntrinsicCurvedManifoldToGraph:

In[23]:=
ResourceFunction["IntrinsicCurvedManifoldToGraph"][ x^4 + y^4, {x, -1, 1}, {y, -1, 1}, 0.3, 200, "PureSpatialGraph"]
Out[23]=

Produce a random sprinkling of 200 points into a 2-dimensional Riemannian manifold with a complicated algebraic curvature function, with discreteness scale 0.3:

In[24]:=
manifold = ResourceFunction["IntrinsicCurvedManifoldToGraph"][ x^2 + 2 y^2 + 3 x^3 + 4 y^4 + 5 x^5 + 6 y^6, {x, -1, 1}, {y, -1, 1}, 0.3, 200]
Out[24]=

Show the complete list of properties:

In[25]:=
manifold["Properties"]
Out[25]=

Show the spatial graph:

In[26]:=
manifold["SpatialGraph"]
Out[26]=

Plot the positions of the sprinkled points only (without spatial edges):

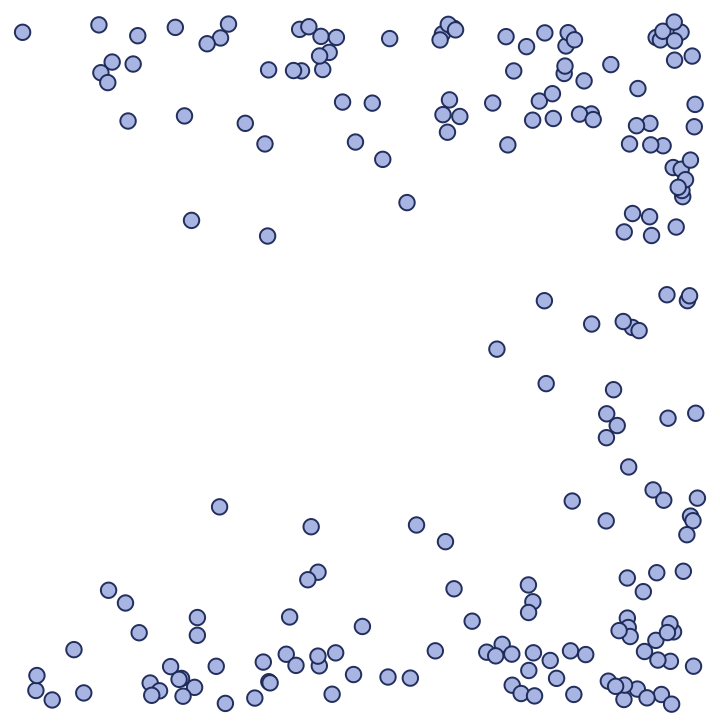
In[27]:=
manifold["Points"]
Out[27]=

Show a complete list of manifold coordinates for the sprinkled points:

In[28]:=
Take[manifold["PointsList"], 100]
Out[28]=

Show the discreteness scale:

In[29]:=
manifold["DiscretenessScale"]
Out[29]=

Show the number of dimensions in the background manifold:

In[30]:=
manifold["Dimensions"]
Out[30]=

Show the total number of spatial edges:

In[31]:=
manifold["EdgeCount"]
Out[31]=

Show the pure spatial graph (with vertex coordinate information removed):

In[32]:=
manifold["PureSpatialGraph"]
Out[32]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 11 December 2020

Source Metadata

  • Citation:
    • Stephen Wolfram (2002), A New Kind of Science
    • Stephen Wolfram (2020), "A Class of Models with Potential to Represent Fundamental Physics"
    • Jonathan Gorard (2020), "Some Relativistic and Gravitational Properties of the Wolfram Model"
    • Jonathan Gorard (2020), "Some Quantum Mechanical Properties of the Wolfram Model"

Related Resources

License Information