Function Repository Resource:

IntervalComplement

Source Notebook

Calculate the complement of intervals

Contributed by: Sander Huisman

ResourceFunction["IntervalComplement"][interval_all,interval₁,interval₂,…]

gives the interval representing all the points of interval_all that are not in any of the interval_i.

Details and Options

ResourceFunction["IntervalComplement"] only works on Interval objects with bounds that are real and not symbolic.

ResourceFunction["IntervalComplement"] supports the intervals to have -∞ and +∞ bounds.

Examples

Basic Examples

Calculate the complement of two intervals:

In[1]:=

Out[1]=

Intervals can be disjoint:

In[2]:=

Out[2]=

Scope

Subtract two Interval objects from another interval object:

In[3]:=

Out[3]=

Subtracting an interval might create a disjoint interval:

In[4]:=

Out[4]=

Unbounded intervals can be used:

In[5]:=

$ResourceFunction["IntervalComplement"][Interval[{0, 10}], Interval[{-\[Infinity], 5}]]$

Out[5]=

In[6]:=

$ResourceFunction["IntervalComplement"][Interval[{0, \[Infinity]}], Interval[{-5, 5}]]$

Out[6]=

In[7]:=

$ResourceFunction["IntervalComplement"][ Interval[{-\[Infinity], \[Infinity]}], Interval[{-5, 5}]]$

Out[7]=

If there is full overlap, an empty interval is returned:

In[8]:=

$ResourceFunction["IntervalComplement"][Interval[{0, 10}], Interval[{-\[Infinity], \[Infinity]}]]$

Out[8]=

An empty interval stays empty:

In[9]:=

Out[9]=

Complementing with an empty interval has no effect:

In[10]:=

Out[10]=

Applications

Calculate the absolute complement of the interval [-5,5] by taking the relative complement with the full interval:

In[11]:=

$a = Interval[{5, -5}]; b = ResourceFunction["IntervalComplement"][ Interval[{-\[Infinity], \[Infinity]}], a]; Quiet[NumberLinePlot[{a, b}]]$

Out[13]=

Properties and Relations

Compare the complement with the union and the intersection of two intervals:

In[14]:=

$a = Interval[{0, 10}]; b = Interval[{5, 15}]; NumberLinePlot[{a, b, IntervalUnion[a, b], IntervalIntersection[a, b], ResourceFunction["IntervalComplement"][a, b], ResourceFunction["IntervalComplement"][b, a]}, PlotLegends -> {"a", "b", "a\[MediumSpace]\[Union]\[MediumSpace]b", "a\[MediumSpace]\[Intersection]\[MediumSpace]b", "a\[MediumSpace]\\\[MediumSpace]b", "b\[MediumSpace]\\\[MediumSpace]a"}]$

Out[16]=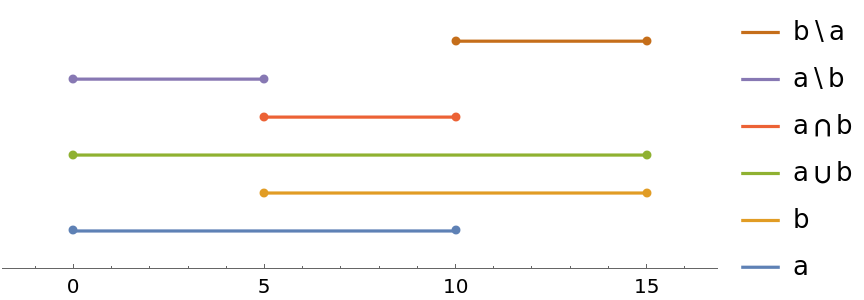

Compare to regular sets:

In[17]:=

$a = Range[0, 10]; b = Range[5, 15]; NumberLinePlot[{a, b, Union[a, b], Intersection[a, b], Complement[a, b], Complement[b, a]}, PlotLegends -> {"a", "b", "a\[MediumSpace]\[Union]\[MediumSpace]b", "a\[MediumSpace]\[Intersection]\[MediumSpace]b", "a\[MediumSpace]\\\[MediumSpace]b", "b\[MediumSpace]\\\[MediumSpace]a"}]$

Out[19]=

Possible Issues

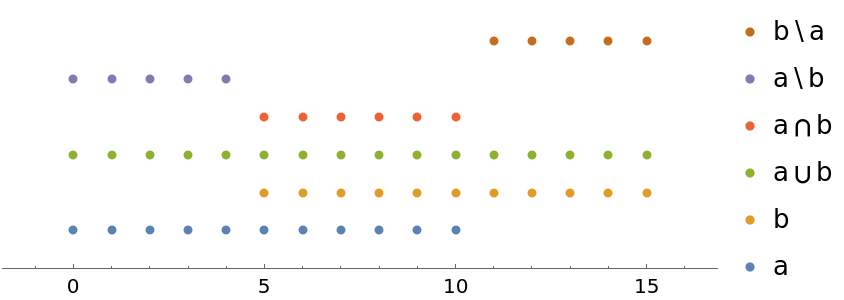Intervals need to be numeric. If the input is symbolic, it will stay unevaluated:

In[20]:=

Out[20]=

Neat Examples

Visualize the subtraction of multiple intervals (red) from a base interval (green):

In[21]:=

$all = Interval[{-2, 3}, {7, 8}, {11, 12}, {15, \[Infinity]}]; other = {Interval[{1.6, 3.1}, {3.5, 4}, {6, 7.5}], Interval[{7.5, 7.75}], Interval[{-\[Infinity], -1}], Interval[{0.1, 0.7}], Interval[{11.5, 17.5}]}; comp = ResourceFunction["IntervalComplement"][all, Sequence @@ other]; NumberLinePlot[ Join[{Style[all, Darker@Green]}, Style[#, Red] & /@ other, {Style[comp, Black]}], PlotLegends -> LineLegend[{Darker@Green, Red, Red, Red, Red, Black}, {"\!$\*SubscriptBox[\(Interval$, $all$]\)", "\!$\*SubscriptBox[\(Interval$, $1$]\)", "\!$\*SubscriptBox[\(Interval$, $2$]\)", "\!$\*SubscriptBox[\(Interval$, $3$]\)", "\!$\*SubscriptBox[\(Interval$, $4$]\)", "Complement"}]]$

Out[24]=

Resource History

Date Created: 22 May 2019

License Information

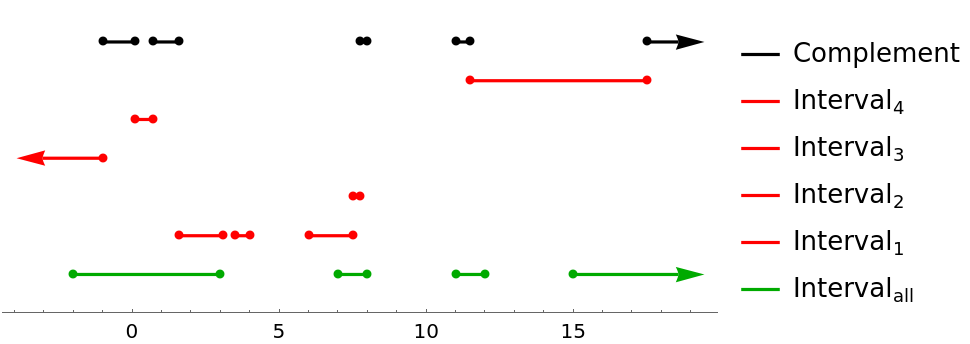This work is licensed under a Creative Commons Attribution 4.0 International License