Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 InterpolatingFunctionToPiecewise

Source Notebook

Convert an InterpolatingFunction to a Piecewise representation

Contributed by: Jan Mangaldan

ResourceFunction["InterpolatingFunctionToPiecewise"][fun,x]

converts the InterpolatingFunction of one variable fun into an equivalent Piecewise polynomial function in x.

Details and Options

ResourceFunction["InterpolatingFunctionToPiecewise"] takes the following options:
"Extrapolation"Falsewhether to extrapolate beyond the initial domain
InterpolationOrderAutomaticorder of polynomial pieces to use
With "Extrapolation"→True, ResourceFunction["InterpolatingFunctionToPiecewise"] yields a piecewise function with a larger domain than the original function.
"Extrapolation"→{bleft,bright} can be used to independently specify the extrapolation behavior on either side of the domain.

Examples

Basic Examples (3) 

Use Interpolation to generate an interpolating function from data:

In[1]:=
f = Interpolation[{1, 2, 3, 5, 8, 5}]
Out[1]=

Convert the result to a Piecewise function:

In[2]:=
pw[x_] = ResourceFunction[ "InterpolatingFunctionToPiecewise", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][f, x]
Out[2]=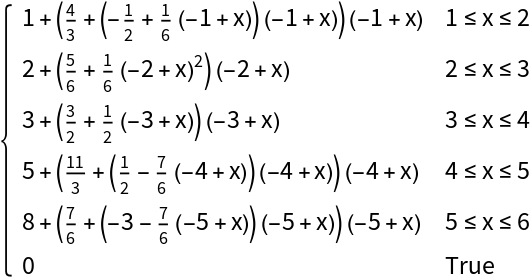

Plot the relative difference between the InterpolatingFunction and the Piecewise function:

In[3]:=
Plot[Abs[(f[x] - pw[x])/f[x]], {x, 1, 6}, PlotRange -> All]
Out[3]=

Scope (2) 

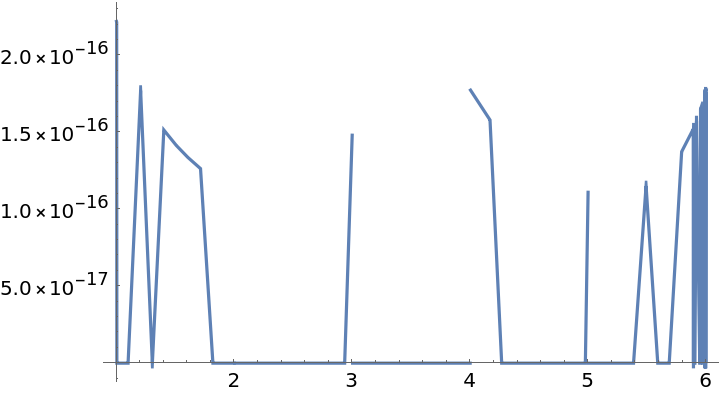Convert an interpolating function from non-equispaced data:

In[4]:=
ResourceFunction[ "InterpolatingFunctionToPiecewise", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ Interpolation[{{0, 0}, {0.1, .3}, {0.5, .6}, {1, -.2}, {2, 3}}, Method -> "Spline"], x]
Out[4]=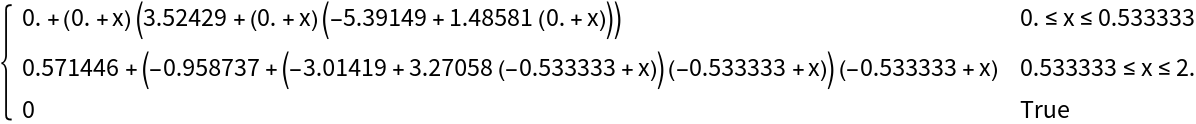

Convert an interpolating function generated by NDSolveValue:

In[5]:=
ResourceFunction[ "InterpolatingFunctionToPiecewise", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ NDSolveValue[{y''[x] + Sin[y[x]] y[x] == 0, y[0] == 1, y'[0] == 0}, y, {x, 0, 5}, Method -> "Extrapolation"], x]
Out[5]=

Options (5) 

Extrapolation (3) 

By default, InterpolatingFunctionToPiecewise generates a result that is valid on the same domain as the original InterpolatingFunction:

In[6]:=
ResourceFunction[ "InterpolatingFunctionToPiecewise", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Interpolation[{1, 2, 3, 5, 8, 5}], x]
Out[6]=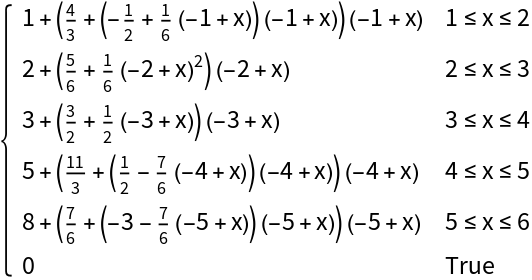

With "Extrapolation"→True, InterpolatingFunctionToPiecewise generates a result with an extended domain:

In[7]:=
ResourceFunction[ "InterpolatingFunctionToPiecewise", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Interpolation[{1, 2, 3, 5, 8, 5}], x, "Extrapolation" -> True]
Out[7]=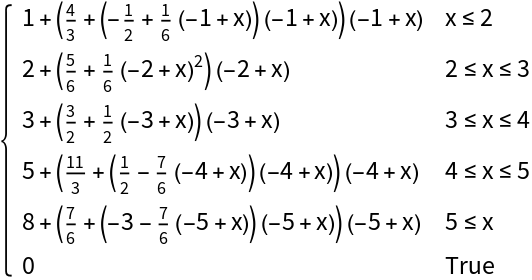

You can give a list of Boolean values to independently specify the extrapolation behavior at the left and right sides of the domain:

In[8]:=
ResourceFunction[ "InterpolatingFunctionToPiecewise", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Interpolation[{1, 2, 3, 5, 8, 5}], x, "Extrapolation" -> {False, True}]
Out[8]=

InterpolationOrder (2) 

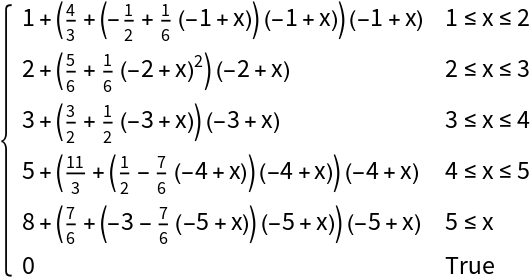Use InterpolationOrder to generate a lower-order approximation to an InterpolatingFunction:

In[9]:=
ResourceFunction[ "InterpolatingFunctionToPiecewise", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ NDSolveValue[{y''[x] + Sin[y[x]] y[x] == 0, y[0] == 1, y'[0] == 0}, y, {x, 0, 5}, Method -> "Extrapolation"], x, InterpolationOrder -> 3]
Out[9]=

Generate a piecewise-constant approximation with InterpolationOrder→0:

In[10]:=
ResourceFunction[ "InterpolatingFunctionToPiecewise", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ Interpolation[{{0, 0}, {0.1, .3}, {0.5, .6}, {1, -.2}, {2, 3}}], x, InterpolationOrder -> 0]
Out[10]=

Possible Issues (1) 

InterpolatingFunctionToPiecewise currently supports only InterpolatingFunction objects of one variable and is left unevaluated otherwise:

In[11]:=
ResourceFunction[ "InterpolatingFunctionToPiecewise", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ Interpolation[{{{0, 0}, 0, {1, 1}}, {{1, 0}, -1, {-1, 1}}, {{0, 1}, -1, {1, -1}}, {{1, 1}, 1, {1, 1}}}], x]
Out[11]=

Version History

  • 1.0.1 – 29 August 2022
  • 1.0.0 – 05 February 2021

Related Resources

License Information