Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 InterpolatingFunctionDomain

Source Notebook

Obtain the domain of an InterpolatingFunction object

Contributed by: Wolfram Staff

ResourceFunction["InterpolatingFunctionDomain"][ifun]

gives the domain for the InterpolatingFunction object ifun.

Details and Options

ResourceFunction["InterpolatingFunctionDomain"] exposes the function by the same name from the package InterpolatingFunctionAnatomy.

Examples

Basic Examples (3) 

Construct an InterpolatingFunction object and obtain its domain:

In[1]:=
Interpolation[{1, 2, 3, 5, 8, 5}]
Out[1]=
In[2]:=
ResourceFunction["InterpolatingFunctionDomain"][%]
Out[2]=

Define a multidimensional interpolation function and find its domain:

In[3]:=
Interpolation[Flatten[Table[{{x, y}, LCM[x, y]}, {x, 4}, {y, 5}], 1]]
Out[3]=
In[4]:=
ResourceFunction["InterpolatingFunctionDomain"][%]
Out[4]=

Get a solution to a differential equation which cannot be computed up to the specified endpoint:

In[5]:=
NDSolve[{x'[t] == Exp[x[t]] - x[t], x[0] == 1}, x, {t, 0, 10}]
Out[5]=
In[6]:=
ifun = First[x /. %]
Out[6]=

Get its domain:

In[7]:=
domain = ResourceFunction["InterpolatingFunctionDomain"][ifun]
Out[7]=

Plot the solution over its domain:

In[8]:=
{begin, end} = domain[[1]]; Plot[ifun[t], {t, begin, end}]
Out[9]=

Properties and Relations (2) 

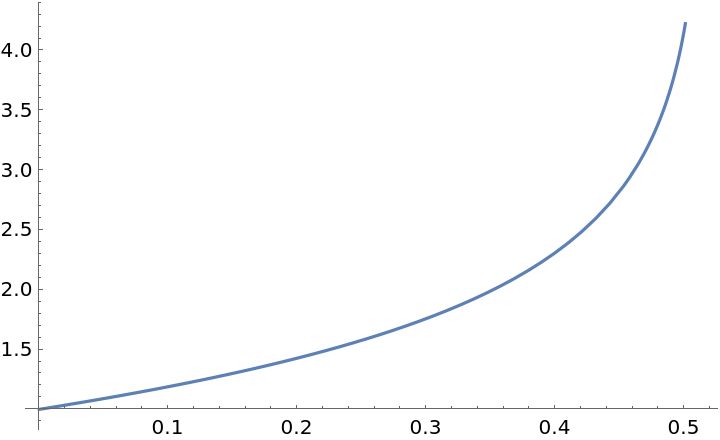The resource function InterpolatingFunctionData returns all the known properties of an InterpolatingFunction object, including its domain:

In[10]:=
ifun = Interpolation[{1, 2, 3, 5, 8, 5}]
Out[10]=
In[11]:=
ResourceFunction["InterpolatingFunctionData"][ifun]
Out[11]=

Compare with InterpolatingFunctionDomain:

In[12]:=
ResourceFunction["InterpolatingFunctionDomain"][ifun]
Out[12]=

Version History

  • 1.0.0 – 24 February 2020

Related Resources

License Information