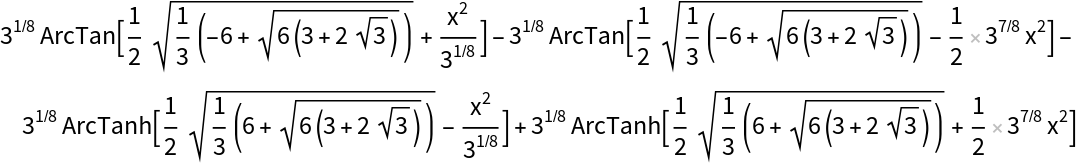Basic Examples (3)
Compute the integral of a rational function:
Compute the integral of a rational function (using Mack's Hermite reduction) where the solution does not contain any logarithmic terms:
Computes a continuous solution to rational integral given in Symbolic Integration I by Manuel Bronstein:
Scope (6)
IntegrateRational can compute many integrals for which Integrate fails to return an elementary form:
In comparison, here's the result from Integrate:
Similarly, the following integral has a concise form from IntegrateRational:
While Integrate expresses the result as a RootSum:
Some integrals will be expressed in finite terms by IntegrateRational, whereas Integrate returns unevaluated:
Integrating some rational functions will introduce algebraic numbers. The solution from IntegrateRational is in the minimal algebraic extension field:
Other integrals will be expressed with hyperbolic arc-tangents:
IntegrateRational works with integrands that contain parameters:
Options (4)
PartialFractions (1)
The option "PartialFractions" specifies if a partial fraction decomposition (with Apart) and term-by-term integration should be used:
Extension (1)
Computing integrals of rational functions using partial fraction decompositions with factorizations over different algebraic extension fields can give alternative forms:
LogToArcTan (2)
By default, sums of complex logarithms are converted into arc-tangents, and sums of real logarithms are converted into hyperbolic arc-tangents:
This feature can be turned off:
Applications (3)
The output from IntegrateRational will be real and continuous on the real line where possible:
Now evaluate at the endpoints 0 and 1, thus effectively computing a closed form for the definite integral 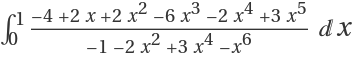 using the Newton-Leibniz theorem:
using the Newton-Leibniz theorem:
By comparison, Integrate gives a substantially more complicated (though equivalent) result:
Verify numerically that this is π:
Use the Newton-Leibniz method to compute alternative forms to Integrate for definite integrals:
Compare to Integrate:
Verify equivalence:
As the result from IntegrateRational is in the minimal algebraic extension field, we know the following integral cannot be expressed without introducing the algebraic number 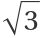 :
:
Properties and Relations (3)
For many simple rational integrals, the result from IntegrateRational and Integrate will often be the same:
Even though a partial fraction decomposition is not immediately possible (via Apart), a concise form for this integral is still possible with IntegrateRational:
Whereas Integrate requires a complete factorization of the denominator of the integrand:
Some integrals will be expressed using Root and RootSum:
Possible Issues (5)
IntegrateRational expands polynomials prior to integration:
The algorithms used by IntegrateRational requires either exact expressions or expressions which rationalize to exact expressions:
The integral of many rational functions will be significantly larger than the integrand:
Sometimes additional simplification is required to express the integral in the minimal algebraic extension field:
Compare the result above to the following result obtained with Rubi:
For some integrals, especially integrals that contain algebraic number coefficients, IntegrateRational may take significantly longer than Integrate:
Further simplification of the result from IntegrateRational may be possible:
Neat Examples (3)
Integrating some rational functions will introduce many logarithms and arc-tangents:
While other rational functions are integrable in terms of algebraic functions without the introduction of new logarithms or arc-tangents:
The following integral cannot be solved without introducing the algebraic number  :
:
Many rational integrals (and algebraic integrals) will have symmetric instances of ArcTan and ArcTanh:
![ResourceFunction["IntegrateRational"][(
x^3 (2 + x^2))/(-2 + Sqrt[3] + (-2 + Sqrt[3]) x^2 - x^4)^2, x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/54551c4a92b600d6.png)
![ResourceFunction["IntegrateRational"][(x^4 - 3 x^2 + 6)/(
x^6 - 5 x^4 + 5 x^2 + 4), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/0308abbe5006163a.png)
![ResourceFunction["IntegrateRational"][(
4 - 2 x - 2 x^2 + 6 x^3 + 2 x^4 - 3 x^5)/(-1 - 2 x^2 + 3 x^4 - x^6),
x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/4be2e137f0359ca8.png)
![Integrate[(
4 - 2 x - 2 x^2 + 6 x^3 + 2 x^4 - 3 x^5)/(-1 - 2 x^2 + 3 x^4 - x^6),
x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/5338dc212f37f542.png)
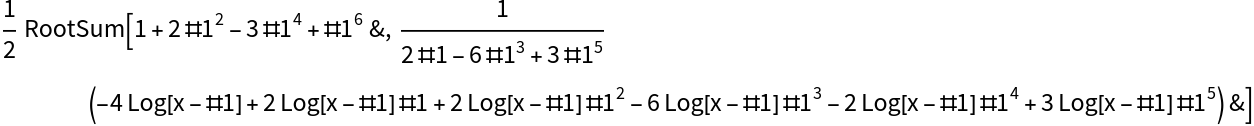
![ResourceFunction["IntegrateRational"][(
2 + 4 x + 4 x^2 + 12 x^3 + 4 x^4 - 6 x^5)/(
1 + 2 x + 2 x^2 - x^4 + x^6), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/3cce122ff648a5f3.png)
![Integrate[(2 + 4 x + 4 x^2 + 12 x^3 + 4 x^4 - 6 x^5)/(
1 + 2 x + 2 x^2 - x^4 + x^6), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/084c08dd16a627dd.png)
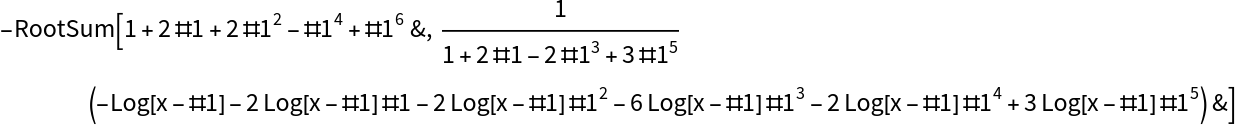
![ResourceFunction["IntegrateRational"][(
32 - 16 Sqrt[3] + 4 x^2 + 2 x^4 + Sqrt[3] x^4)/((4 + x^2) (144 - 80 Sqrt[3] + 24 x^2 + 9 x^4 + 5 Sqrt[3] x^4)), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/06f1b6000b27e9fa.png)
![Integrate[(
32 - 16 Sqrt[3] + 4 u^2 + 2 u^4 + Sqrt[3] u^4)/((4 + u^2) (144 - 80 Sqrt[3] + 24 u^2 + 9 u^4 + 5 Sqrt[3] u^4)), u]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/18c1f6589939ce98.png)
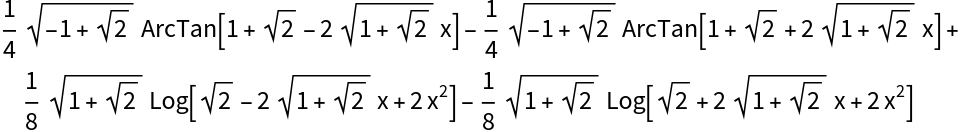
![ResourceFunction["IntegrateRational"][(
5 - 6 x^2 - 12 x^5 - 15 x^6 + 10 x^9)/(
1 + 5 x^2 - 4 x^3 - 3 x^4 - 10 x^5 + 6 x^6 + 5 x^8 - 4 x^9 + x^12),
x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/731c12f57d64cc82.png)
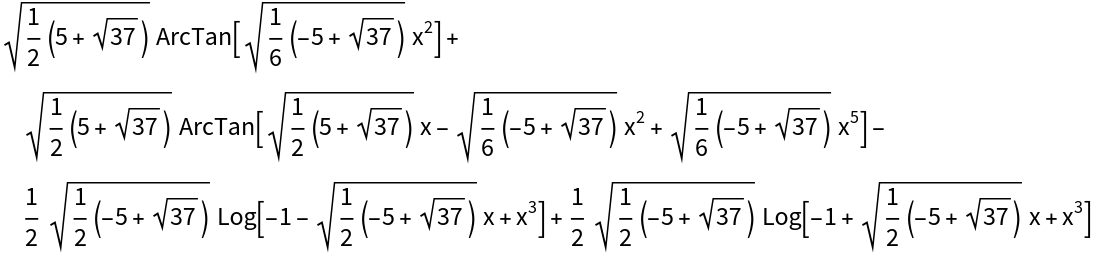
![ResourceFunction[
"IntegrateRational"][(-72 Sqrt[2] + 480 Sqrt[3] x + 24 Sqrt[2] x^2)/(-564 - 144 Sqrt[6] x + 840 x^2 + 48 Sqrt[6] x^3 - 144 x^4), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/37675424bd308379.png)
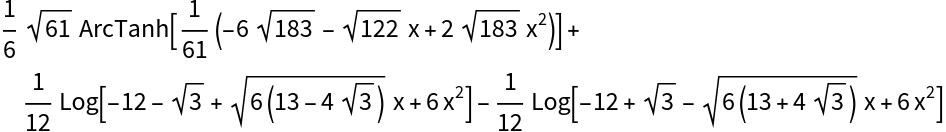
![ResourceFunction["IntegrateRational"][(a x + b)/(b^4 x^4 - a^4), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/63fcf55af9381153.png)
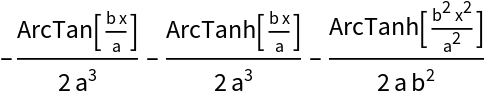
![ResourceFunction["IntegrateRational"][(2 x + x^2)/(
2 + 4 x + 2 x^2 + x^4), x, "PartialFractions" -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/023206d199c3b984.png)
![ResourceFunction["IntegrateRational"][(2 x + x^2)/(
2 + 4 x + 2 x^2 + x^4), x, "PartialFractions" -> True, Extension -> Sqrt[3 + 2 Sqrt[2]]]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/49cedf121c8a63ee.png)

![case = ResourceFunction[
"IntegrateRational"][(-4 + 2 x + 2 x^2 - 6 x^3 - 2 x^4 + 3 x^5)/(-1 - 2 x^2 + 3 x^4 - x^6), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/1a04c9e3f87b2ea8.png)
![]() using the Newton-Leibniz theorem:
using the Newton-Leibniz theorem:![case2 = Integrate[(-4 + 2 x + 2 x^2 - 6 x^3 - 2 x^4 + 3 x^5)/(-1 - 2 x^2 + 3 x^4 - x^6), {x, 0, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/1ee90886369fdea8.png)
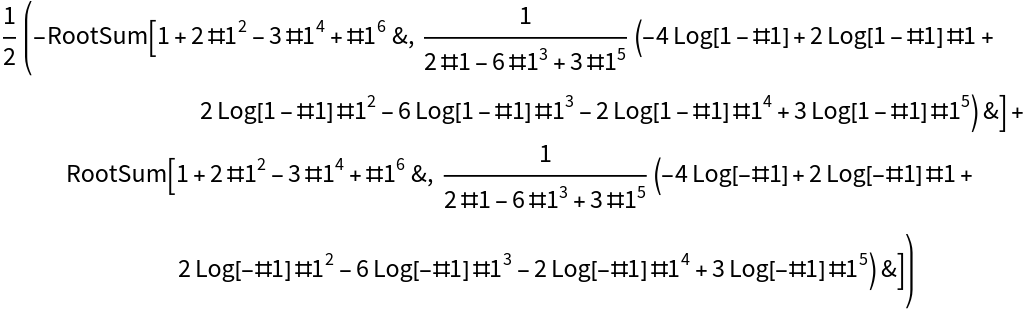
![case = ResourceFunction["IntegrateRational"][(-1 + 2 x^2)/(
1 - x^2 + x^4), x];
res1 = (case /. x -> 1) - (case /. x -> -1)](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/497bf0d617f38c2b.png)
![]() :
:![ResourceFunction["IntegrateRational"][(1 - 3 x^2 - 3 x^4 + x^6)/(
1 - 5 x^2 + 9 x^4 - 5 x^6 + x^8), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/738751907816dd9e.png)
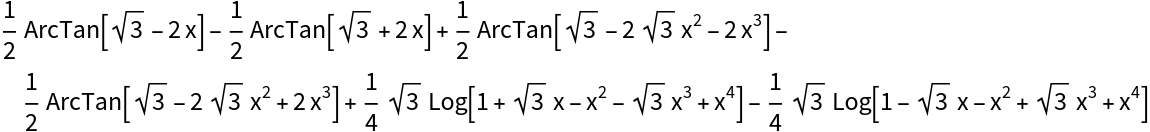
![ResourceFunction[
"IntegrateRational"][(-1 + 5 x + 12 x^2 + 8 x^3 + 2 x^4)/(-3 - 3 x + 6 x^2 + 17 x^3 + 15 x^4 + 6 x^5 + x^6), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/533ead2a7a7c1aed.png)

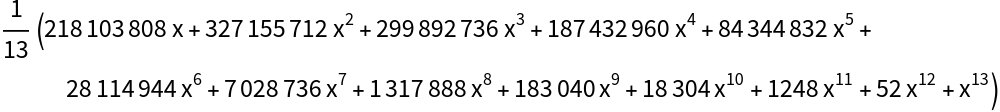
![ResourceFunction[
"IntegrateRational"][(-2 - 4 x + x^2)/(-4 - 8 x + x^2 + 5 x^3 + 10 x^4), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/78b47754fe42d829.png)

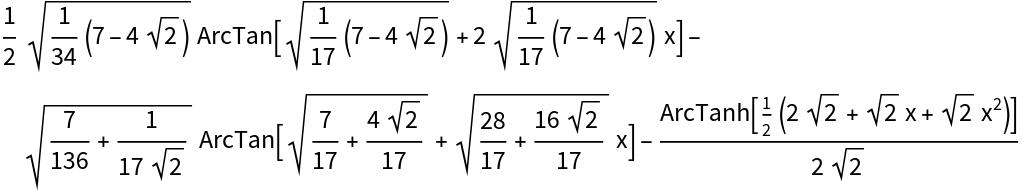
![D[-(ArcTan[(1 + 2 x)/Sqrt[7 - 4 Sqrt[2]]]/(
2 Sqrt[2 (7 - 4 Sqrt[2])])) + ArcTan[(1 + 2 x)/Sqrt[7 + 4 Sqrt[2]]]/(2 Sqrt[2 (7 + 4 Sqrt[2])]) -
ArcTanh[(7 + 4 (1/2 + x)^2)/(4 Sqrt[2])]/(2 Sqrt[2]), x] // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/675452c50acc84f3.png)
![ResourceFunction["IntegrateRational"][(-8 Sqrt[30] - 8 Sqrt[3] x)/(
12 Sqrt[5] + 12 Sqrt[2] x - 8 x^2), x] // Timing](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/1ce5c0742364d3bc.png)
![Integrate[(-8 Sqrt[30] - 8 Sqrt[3] x)/(
12 Sqrt[5] + 12 Sqrt[2] x - 8 x^2), x] // Timing](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/1bcfb0a902160097.png)
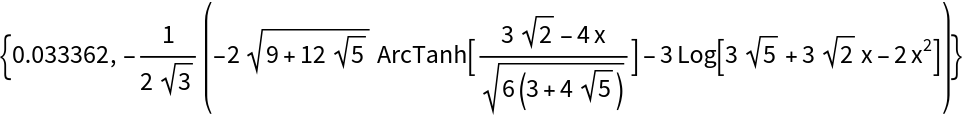
![integrateRationalResult = ResourceFunction["IntegrateRational"][(-8 Sqrt[30] - 8 Sqrt[3] x)/(
12 Sqrt[5] + 12 Sqrt[2] x - 8 x^2), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/0a153348e4efb1ed.png)
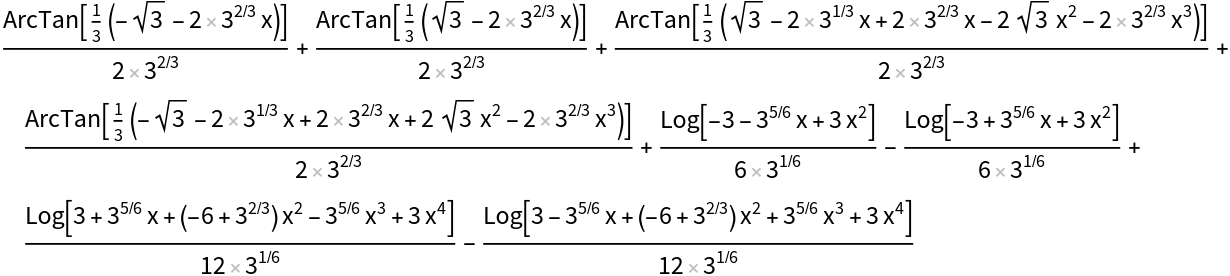
![ResourceFunction["IntegrateRational"][(
16 - 429 x^8 + 1287 x^10 - 1287 x^12 + 429 x^14)/(
x^8 (1 - 4 x^2 + 6 x^4 - 4 x^6 + x^8)), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/4a85f4f2d5b7666b.png)
![]() :
:![ResourceFunction[
"IntegrateRational"][(-4 - 6 x^2 + 4 x^4 - 2 x^6 - 40 x^8 + 14 x^10 - 6 x^12)/(
1 + 2 x^2 + x^4 - 16 x^6 + 2 x^8 - 2 x^10 + 4 x^12 - 4 x^14 + x^16),
x] // ToRadicals](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/4c36bfb3164f26b3.png)
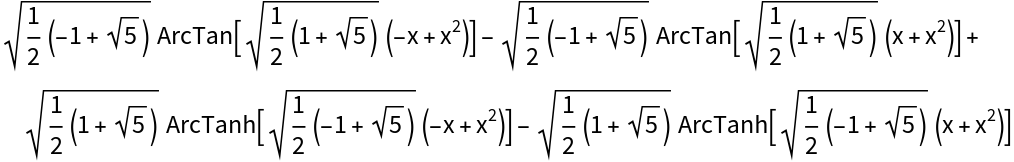
![ResourceFunction[
"IntegrateRational"][(-80 (-3 + 2 Sqrt[3]) x - 80 (3 - 2 Sqrt[3]) x^3 - 80 (90 + 30 Sqrt[3]) x^5 - 960 Sqrt[3] x^7 - 7440 Sqrt[3] x^9 - 1440 Sqrt[3] x^11)/(14 - 8 Sqrt[3] + (-28 + 20 Sqrt[3]) x^2 + (-1110 - 418 Sqrt[3]) x^4 + (296 - 268 Sqrt[3]) x^6 + (434 - 2401 Sqrt[3]) x^8 + (204 - 828 Sqrt[3]) x^10 + (-324 - 468 Sqrt[3]) x^12 - 432 x^14 + 648 x^16), x]](https://www.wolframcloud.com/obj/resourcesystem/images/768/768a327c-5a00-4326-89d1-d914eb32fe9c/5f0a978516118b35.png)