Basic Examples (1) 

Perform a partial fraction decomposition:

In[1]:=

Out[1]=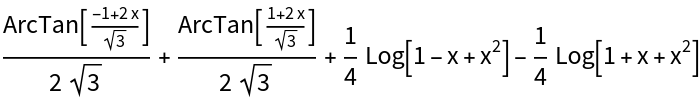

Scope (3) 

In this example we compute the partial fraction expansion prior to computing the integral with Integrate:

In[2]:=

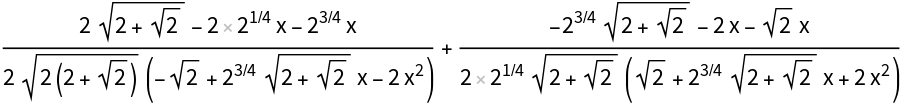
Out[2]=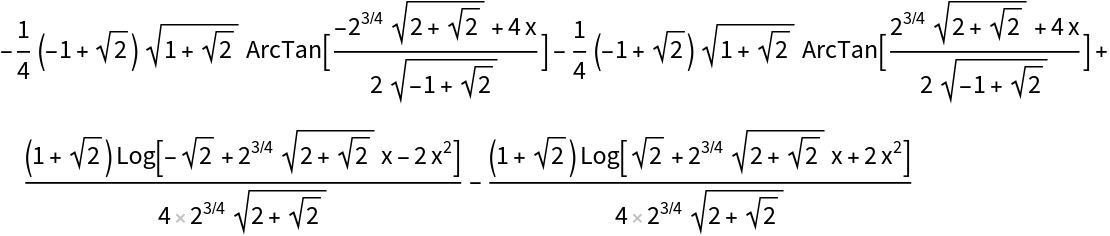

IntegratePFD gives different results than Integrate:

In[3]:=

Out[3]=

In[4]:=

Out[4]=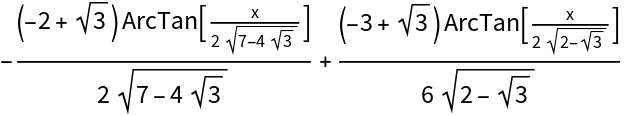

Another example:

In[5]:=

Out[5]=

In[6]:=

Out[6]=

Options (2) 

Extension (2) 

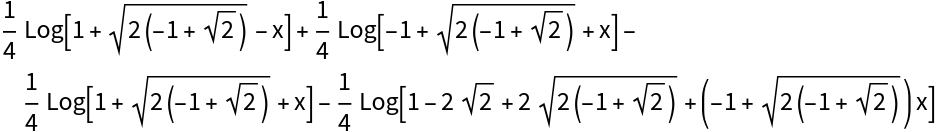By default this integral produced an ArcTan, as expected:

In[7]:=

Out[7]=

With the following extension we factor x²+1 into (x-I)(x+I) prior to computing the partial fraction decomposition:

In[8]:=

Out[8]=

Applications (1) 

Compute the integral over different algebraic number fields until you find a solution which matched your homework problem:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

In[11]:=

Out[11]=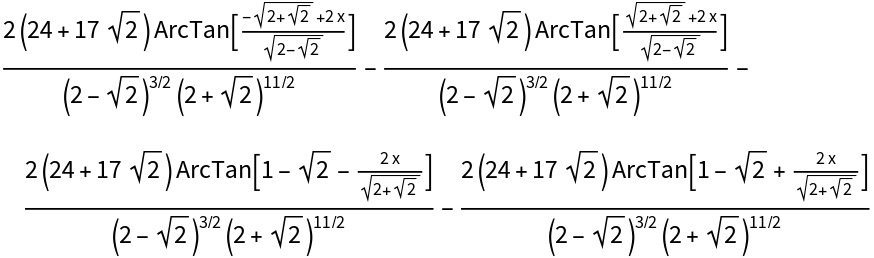

In[12]:=

Out[12]=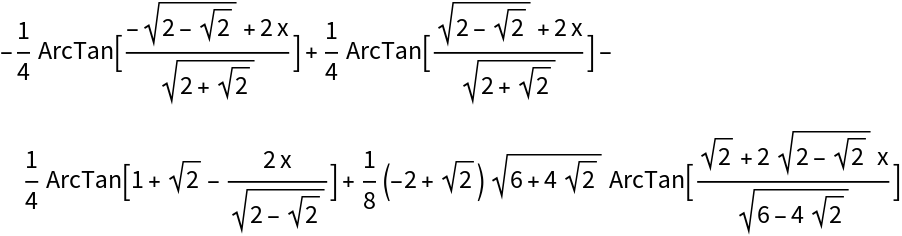

Properties and Relations (2) 

Integrate and IntegratePFD will both return valid antiderivatives, however the results will often look vastly different:

In[13]:=

Out[13]=

In[14]:=

Out[14]=

The two results are equivalent:

In[15]:=

Out[15]=

Possible Issues (1) 

Sometimes Integrate will give a more concise answer than IntegratePFD:

In[16]:=

Out[16]=

In[17]:=

Out[17]=

Neat Examples (1) 

IntegratePFD may be used to generate many alternative forms of an integral by factoring the denominator over different algebraic number fields:

In[18]:=

Out[18]=

In[19]:=

Out[19]=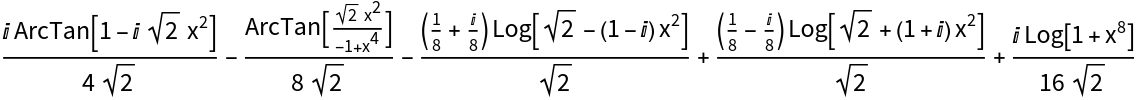

In[20]:=

Out[20]=

In[21]:=

Out[21]=

In[22]:=

Out[22]=

In[23]:=

Out[23]=

In[24]:=

Out[24]=