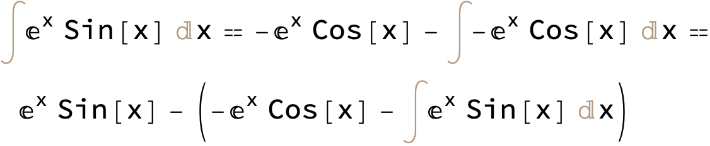Get an inactive expression representing an integration by parts
Contributed by:
Wolfram|Alpha Math Team
Examples
Basic Examples (2)
Integrate 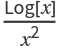 by parts:
by parts:
Use Activate to evaluate the result:
Integrate xⅇx by parts on the domain 0≤x≤1:
Use Activate to fully evaluate the integral:
Scope (1)
To view the particular u and dv that were used to integrate by parts, use the optional third argument "Grid":
Options (2)
Use the option "ShowOtherDecompositions" to return a list of possible integrations by parts:
The optional third argument "Grid" can be combined with the option "ShowOtherDecompositions":
Applications (1)
Prove the reduction formula:
Possible Issues (2)
IntegrateByParts will return results, sometimes by the trivial decomposition u⩵expr and ⅆv⩵1ⅆx:
If the given definite integral does not converge on the domain given, IntegrateByParts returns unevaluated with a message:
Neat Examples (4)
Compute an integral by integrating by parts twice:
Choose 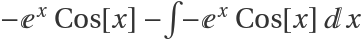 and then integrate by parts again:
and then integrate by parts again:
Therefore we have:
Which can be simplified to:
Publisher
Wolfram|Alpha Math Team
Version History
-
2.0.0
– 23 March 2023
-
1.0.0
– 01 April 2020
![]() by parts:
by parts: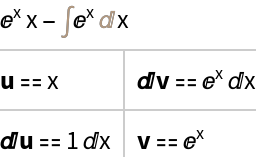

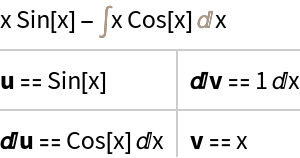
![]() and then integrate by parts again:
and then integrate by parts again: