Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 IntegrateByParts

Source Notebook

Get an inactive expression representing an integration by parts

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["IntegrateByParts"][f,x]

returns the Inactive indefinite integration by parts of f with respect to x.

ResourceFunction["IntegrateByParts"][f,{x,xmin,xmax}]

returns the Inactive definite integration by parts of f with respect to x from xmin to xmax.

ResourceFunction["IntegrateByParts"][f,x|{x,xmin,xmax},"Grid"]

returns the Inactive integration by parts in a Grid highlighting the particular of u and dv that were used.

Details and Options

Integration by parts is a technique for computing integrals, both definite and indefinite, that makes use of the chain rule for derivatives.
For an integral , choose u and ⅆv such that f[x]ⅆx⩵ uⅆv. Then, by computing ⅆu and integrating ⅆv to get v, we can write .

Examples

Basic Examples (2) 

Integrate by parts:

In[1]:=
ResourceFunction["IntegrateByParts"][Log[x]/x^2, x]
Out[1]=

Use Activate to evaluate the result:

In[2]:=
Activate[%]
Out[2]=

Integrate xⅇx by parts on the domain 0≤x≤1:

In[3]:=
ResourceFunction["IntegrateByParts"][x Exp[x], {x, 0, 1}]
Out[3]=

Use Activate to fully evaluate the integral:

In[4]:=
Activate[%]
Out[4]=

Scope (1) 

To view the particular u and dv that were used to integrate by parts, use the optional third argument "Grid":

In[5]:=
ResourceFunction["IntegrateByParts"][x Exp[x], x, "Grid"]
Out[5]=

Options (2) 

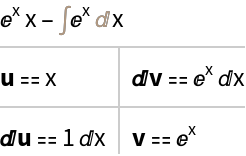Use the option "ShowOtherDecompositions" to return a list of possible integrations by parts:

In[6]:=
ResourceFunction["IntegrateByParts"][x Exp[x], {x, 0, 1}, "ShowOtherDecompositions" -> True]
Out[6]=

The optional third argument "Grid" can be combined with the option "ShowOtherDecompositions":

In[7]:=
ResourceFunction["IntegrateByParts"][x Exp[x], {x, 0, 1}, "Grid", "ShowOtherDecompositions" -> True]
Out[7]=

Applications (1) 

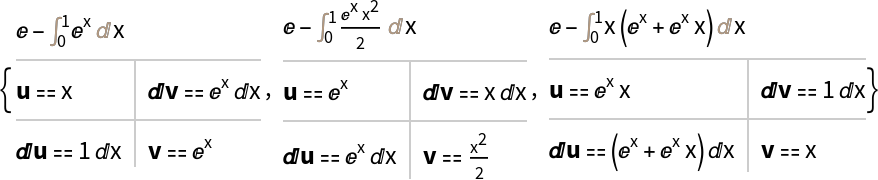Prove the reduction formula:

In[8]:=
ResourceFunction["IntegrateByParts"][Sin[x]^n, x]
Out[8]=

Possible Issues (2) 

IntegrateByParts will return results, sometimes by the trivial decomposition u⩵expr and ⅆv⩵1ⅆx:

In[9]:=
ResourceFunction["IntegrateByParts"][Sin[x], x, "Grid"]
Out[9]=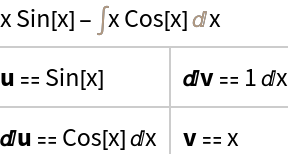

If the given definite integral does not converge on the domain given, IntegrateByParts returns unevaluated with a message:

In[10]:=
ResourceFunction["IntegrateByParts"][Log[x]/x^2, {x, 0, 2}]
Out[10]=

Neat Examples (6) 

Compute an integral by integrating by parts twice:

In[11]:=
ResourceFunction["IntegrateByParts"][E^x Sin[x], x, "ShowOtherDecompositions" -> True]
Out[11]=

Choose and then integrate by parts again:

In[12]:=
ResourceFunction["IntegrateByParts"][-E^x Cos[x], x]
Out[12]=

Therefore we have:

==-ⅇx Cos[x]-==ⅇx Sin[x]-(-ⅇx Cos[x]-)

Which can be simplified to:

2* == ⅇx (Sin[x]+Cos[x])

Publisher

Wolfram|Alpha Math Team

Version History

  • 2.0.0 – 23 March 2023
  • 1.0.0 – 01 April 2020

License Information