Basic Examples (4)
This is a well-known pseudo-elliptic integral:
Some integrals are expressed as a rational function of x and the radicals in the integrand:
Other integrals can be expressed in terms of Log, ArcTan and ArcTanh:
The following is an Abelian integral:
Scope (15)
IntegrateAlgebraic can integrate all integrands in 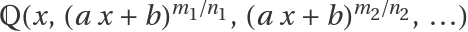 regardless of their size or complexity:
regardless of their size or complexity:
IntegrateAlgebraic can integrate all integrands in 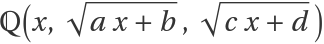 :
:
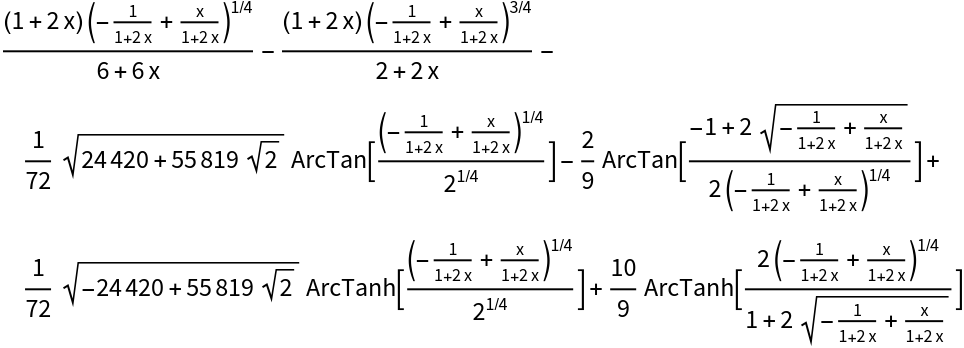
IntegrateAlgebraic can integrate all integrands in 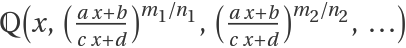 :
:
IntegrateAlgebraic can integrate all integrands in 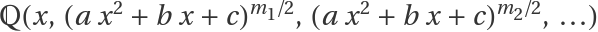 , as these are converted to rational functions via Euler’s substitution:
, as these are converted to rational functions via Euler’s substitution:
For the following integral, IntegrateAlgebraic uses the substitution 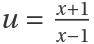 to reduce the integral to
to reduce the integral to 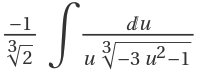 :
:
For the following integral, IntegrateAlgebraic uses the substitution 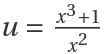 to reduce the integral to
to reduce the integral to 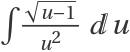 :
:
For the following integral, IntegrateAlgebraic uses the substitution 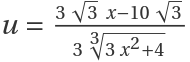 to reduce the integral to
to reduce the integral to 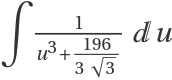 :
:
Some integrals will introduce algebraic numbers that are not present in the integrand:
IntegrateAlgebraic works with radicals other than square roots:
Some integrals will be expressed in terms of RootSum expressions:
IntegrateAlgebraic can often work with parameters in the integrand:
IntegrateAlgebraic has a limited ability to integrate nested radicals:
IntegrateAlgebraic can succeed on some integrals where the Risch-Bronstein-Trager algorithm struggles:
IntegrateAlgebraic can handle many otherwise difficult integrals involving parameters:
IntegrateAlgebraic can handle many integrals when the radicand is a rational function:
Options (9)
Expansion (2)
The option "Expansion" → True specifies if the integrals is expanded and integrated term-by-term after exhausting all other possible methods. By default "Expansion" is False, as this method may require many time consuming recursive calls to IntegrateAlgebraic:
With "Expansion" → True, IntegrateAlgebraic may return partial results:
DegreeBound (2)
The default for "DegreeBound" is 8:
Increasing the degree bound can solve some large Abelian integrals:
Elementary (1)
"Elementary" specifies if the solution should be composed of elementary functions only. By default "Elementary" is True:
SingleStepTimeConstraint (1)
The option "SingleStepTimeConstraint" specifies the time in seconds that IntegrateAlgebraic spends in various computationally-intensive routines. The default for "SingleStepTimeConstraint" is 0.25. Increasing this time constraint may solve some integrals that otherwise return unevaluated:
SubstitutionSize (2)
The option "SubstitutionSize" determines the number of rational substitutions tried within IntegrateAlgebraic. By default "SubstitutionSize" is "Small". Other settings are "Medium" and "Large". By default, the Laurent polynomial substitution code considers a polynomial with 3 terms only:
With "SubstitutionSize"→"Medium", we use a Laurent polynomial substitution with 4 terms:
VerifySolutions (1)
VerifySolutions numerically verifies the solution obtained by IntegrateAlgebraic. By default this is False. Verifying the solution will increase the runtime of IntegrateAlgebraic:
Applications (1)
If the integral is continuous, then the definite integral can be computed using Newton–Leibniz:
Possible Issues (3)
Some integrals will take longer than others:
Trager’s Hermite reduction will always find the rational (algebraic) part of the integral, whereas the methods used by IntegrateAlgebraic will sometimes fail:
IntegrateAlgebraic will fail to compute some algebraic integrals which possess elementary solutions:
Neat Examples (2)
Some integrals require many logarithms (including ArcTan and ArcTanh):
Some integrals introduce complicated algebraic numbers:
![ResourceFunction[
"IntegrateAlgebraic"][(-1 + x^2)/((1 + x^2) Sqrt[1 + x^4]), x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/5c18e931354c035d.png)
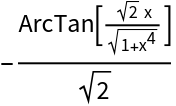
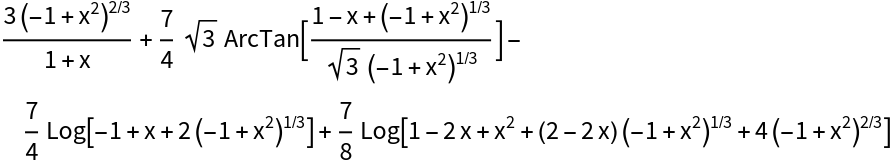
![]() regardless of their size or complexity:
regardless of their size or complexity: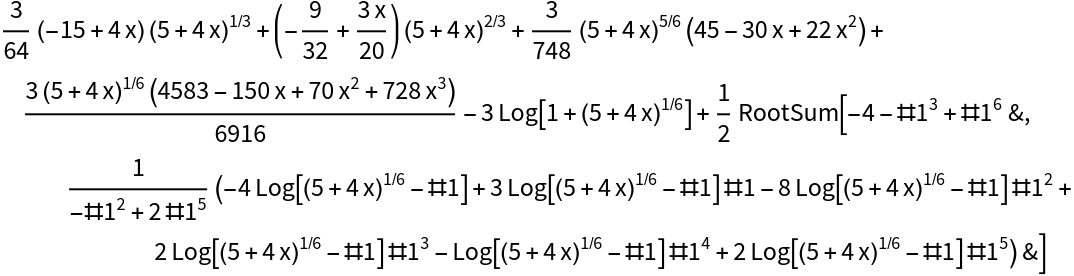
![]() :
: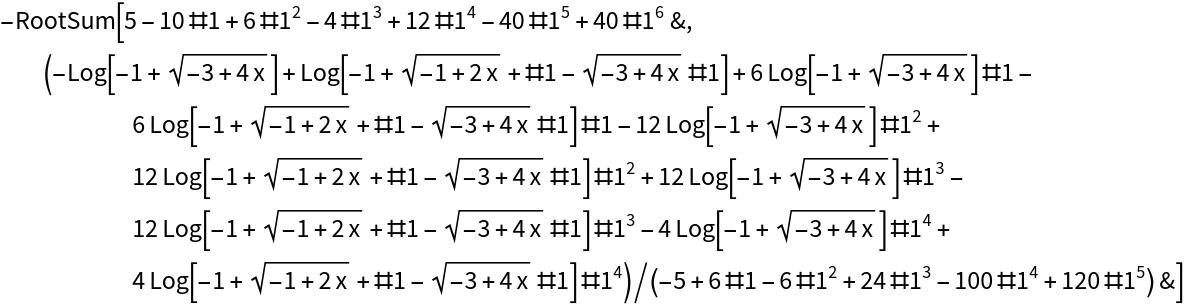
![]() :
:![ResourceFunction[
"IntegrateAlgebraic"][(((x - 1)/(2 x + 1))^(1/4) - 3 ((x - 1)/(2 x + 1))^(3/4))/((x - 1) (x + 1)^2 (2 x - 1)), x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/15dd66819436f4aa.png)
![]() , as these are converted to rational functions via Euler’s substitution:
, as these are converted to rational functions via Euler’s substitution:![ResourceFunction["IntegrateAlgebraic"][(
Sqrt[x^2 - 4 x + 1] + (x^2 - 4 x + 1)^(3/2))/(
Sqrt[x^2 - 4 x + 1] - (x^2 - 4 x + 1)^(5/2) + (x^2 - 4 x + 1)^(3/2)),
x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/6a6180d42d4951c0.png)
![]() to reduce the integral to
to reduce the integral to ![]() :
: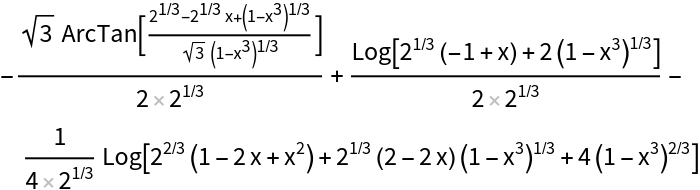
![]() to reduce the integral to
to reduce the integral to ![]() :
:![ResourceFunction[
"IntegrateAlgebraic"][((-2 + x^3) Sqrt[1 - x^2 + x^3])/(1 + x^3)^2,
x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/53e5b9f3c3bcf3f5.png)
![]() to reduce the integral to
to reduce the integral to ![]() :
: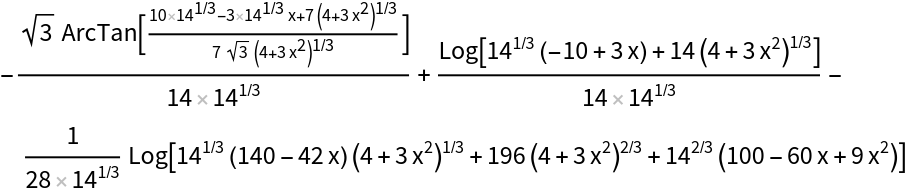
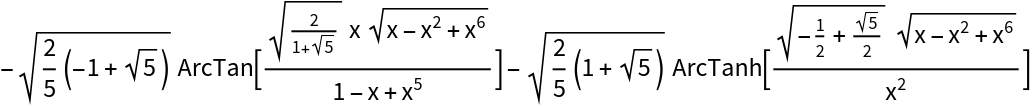
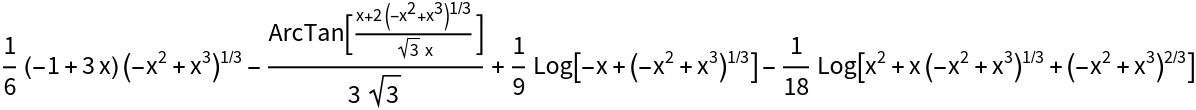
![ResourceFunction[
"IntegrateAlgebraic"][((2 c - a x^3) Sqrt[
a x^3 + b x^2 + c])/((a x^3 + (b - 3) x^2 + c) (a x^3 + (b - 2) x^2 + c)), x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/0fb170bf08b65bf9.png)
![ResourceFunction["IntegrateAlgebraic"][Sqrt[
Sqrt[x^2 + 1] + 1]/((x - 1) Sqrt[x^2 + 1]), x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/243a11c657f763d5.png)
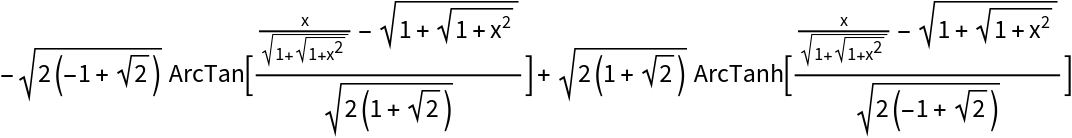
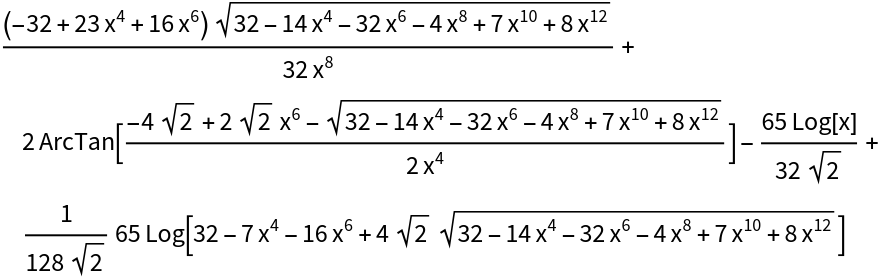
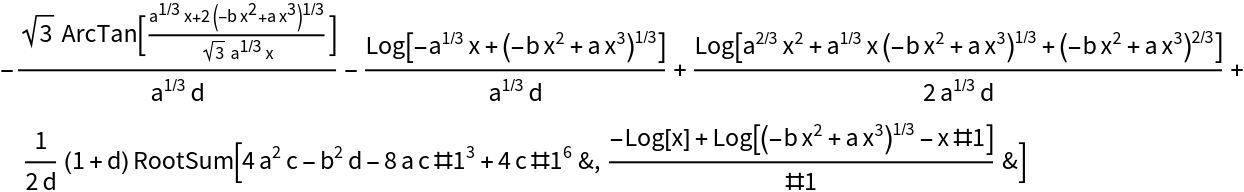
![ResourceFunction["IntegrateAlgebraic"][((-2 + x) (1 - x + x^2))/(
x^3 (-1 + x + x^2) ((1 - x + 2 x^2)/(1 - x + 3 x^2))^(1/3)), x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/58856618f50fa5b3.png)
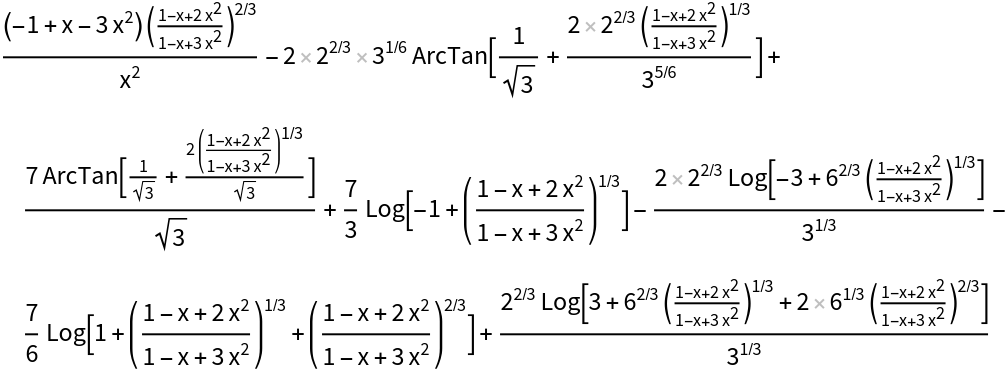
![ResourceFunction[
"IntegrateAlgebraic"][(-36 - 6 x^2 + 6 x^3 + x^6)/(x (-6 + x^3) (36 - 90 x + 122 x^2 - 96 x^3 + 51 x^4 - 26 x^5 + 15 x^6 - 6 x^7 + x^8) ((6 + x^3)/(-6 + x^3))^(1/6)), x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/422166f59b36cbb9.png)
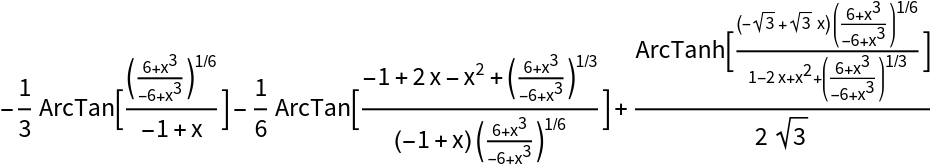
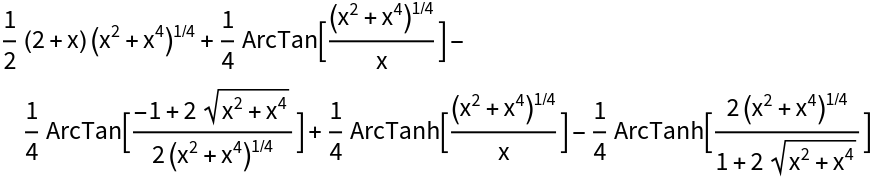

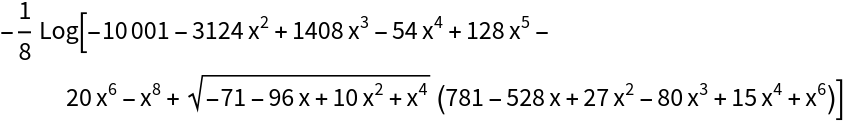
![ResourceFunction["IntegrateAlgebraic"][(29 x^2 + 18 x - 3)/Sqrt[
x^6 + 4 x^5 + 6 x^4 - 12 x^3 + 33 x^2 - 16 x], x, "DegreeBound" -> 30]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/2db984dc37a4840b.png)
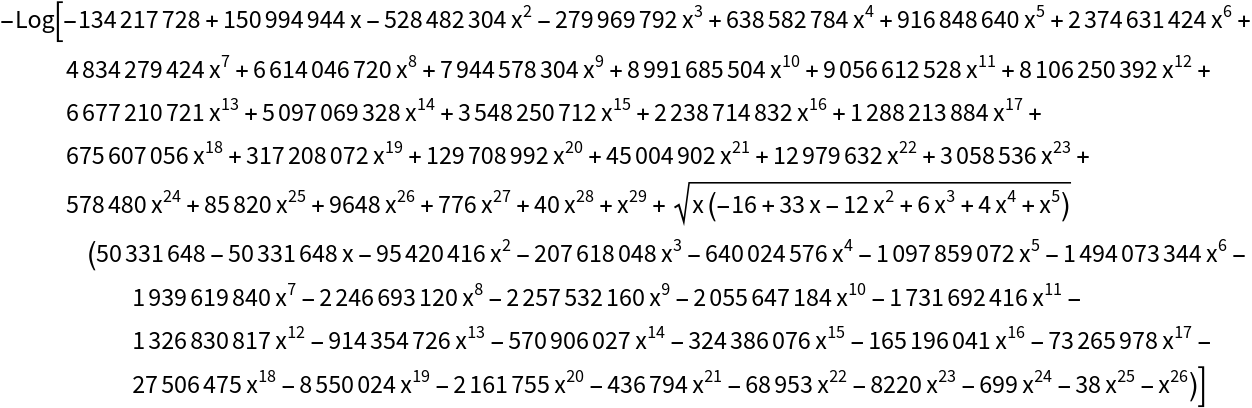
![ResourceFunction["IntegrateAlgebraic"][(39 x^2 + 9 x - 1)/Sqrt[
x^6 + 4 x^4 + 10 x^3 + 4 x^2 - 4 x + 1], x, "DegreeBound" -> 40]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/122711bfa9b075ce.png)

![ResourceFunction["IntegrateAlgebraic"][(
6 x^8 + 1)/((2 x^8 - 1) Power[
4 x^16 + 2 x^10 - 4 x^8 - x^4 - x^2 + 1, (4)^-1]), x, "Elementary" -> False] // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/4b97a75f1cda0828.png)
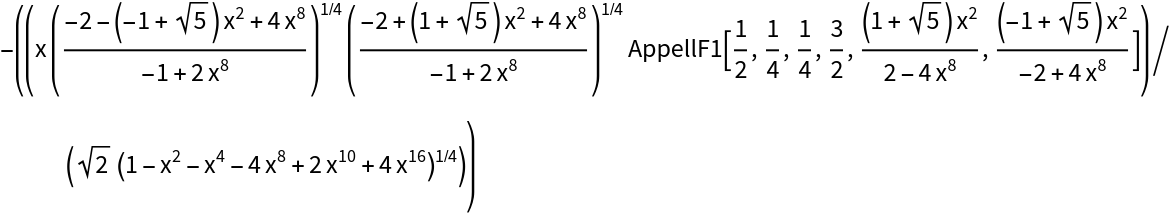
![ResourceFunction[
"IntegrateAlgebraic"][(1 + x^4)^2/((-1 + x^4)^2 Sqrt[
x^2 + Sqrt[1 + x^4]]), x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/5c75514fc50fb478.png)
![ResourceFunction[
"IntegrateAlgebraic"][(1 + x^4)^2/((-1 + x^4)^2 Sqrt[
x^2 + Sqrt[1 + x^4]]), x, "SingleStepTimeConstraint" -> 0.5]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/2b53b224ce706880.png)
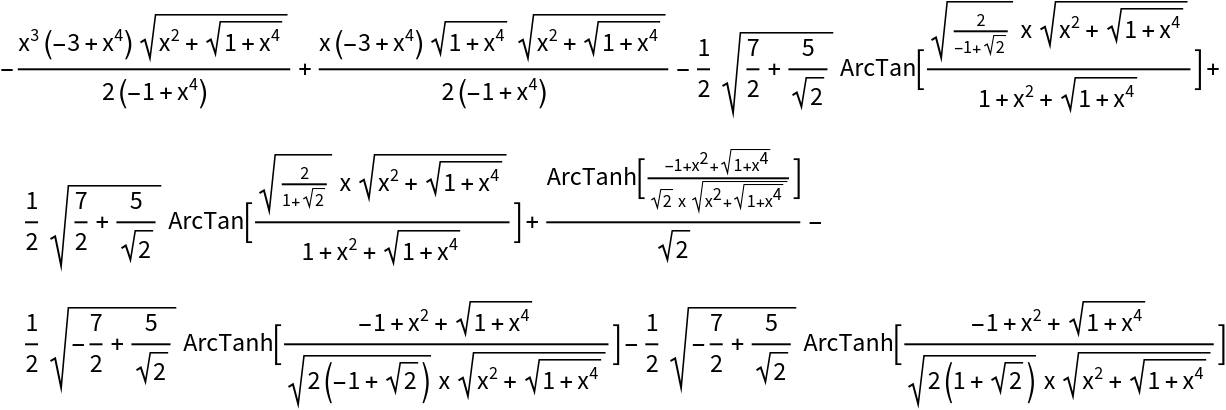
![ResourceFunction[
"IntegrateAlgebraic"][((-1 + x^2 + 2 x^3 + 3 x^4) (1 - 2 x + x^2 + x^4 + 3 x^6 + 2 x^7 + x^8))/(x Sqrt[
1 - 2 x + 2 x^2 + x^4 + 3 x^6 + 2 x^7 + x^8] (1 - 2 x + 4 x^2 + x^4 + 3 x^6 + 2 x^7 + x^8)), x, "RationalUndeterminedOnly" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/50a158633bd42628.png)
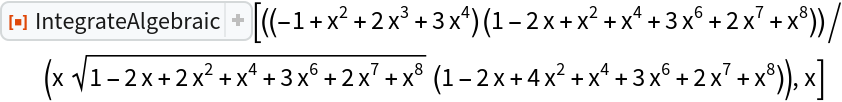
![ResourceFunction[
"IntegrateAlgebraic"][((-1 + x^2 + 2 x^3 + 3 x^4) (1 - 2 x + x^2 + x^4 + 3 x^6 + 2 x^7 + x^8))/(x Sqrt[
1 - 2 x + 2 x^2 + x^4 + 3 x^6 + 2 x^7 + x^8] (1 - 2 x + 4 x^2 + x^4 + 3 x^6 + 2 x^7 + x^8)), x, "SubstitutionSize" -> "Medium", "RationalUndeterminedOnly" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/050174b2ace232c0.png)

![ResourceFunction["IntegrateAlgebraic"][Sqrt[x^3 + 1]/x, x, VerifySolutions -> False] // Timing // First
ResourceFunction["IntegrateAlgebraic"][Sqrt[x^3 + 1]/x, x, VerifySolutions -> True] // Timing // First](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/13ae078cc8df2531.png)
![ResourceFunction[
"IntegrateAlgebraic"][((x^4 - 1) Sqrt[1 + x^4])/(1 + 3 x^2 + x^4)^2,
x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/6b57fbfd425b787a.png)
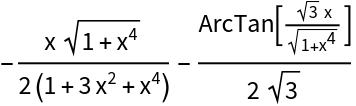
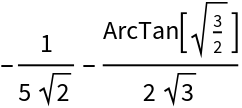
![% - NIntegrate[((x^4 - 1) Sqrt[1 + x^4])/(1 + 3 x^2 + x^4)^2, {x, 0, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/13550a6ce5647ca0.png)
![]() and a candidate substitution of the form
and a candidate substitution of the form ![]() . The following computation shows that we can reduce
. The following computation shows that we can reduce ![]() to
to ![]() , where
, where ![]() :
:![]() to evaluate the integral
to evaluate the integral ![]() :
:![GroebnerBasis[{Dt[y] == (x^2 - x + 1)/((x^2 - 1) Sqrt[x^3 + x]) Dt[x],
u == (x^2 + 1)/x, Dt[u == (x^2 + 1)/x]}, {u, Dt[u]}, {Dt[x], x}, MonomialOrder -> EliminationOrder, Method -> "Buchberger"]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/3b2a31eb743e09b9.png)
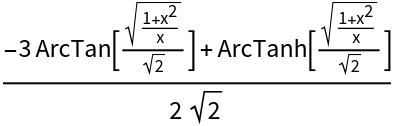
![ResourceFunction["IntegrateAlgebraic"][(
x^2 - x + 1)/((x^2 - 1) Sqrt[x^3 + x]), x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/019ff6ce92299585.png)
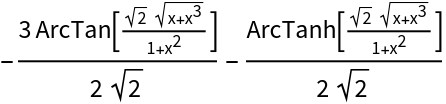
![ResourceFunction["IntegrateAlgebraic"][(
2 x^2 + x + 2)/((2 x - 1) Sqrt[x^4 + x]), x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/5bf0dbf9a4b3fcad.png)
![Integrate[(2 x^2 + x + 2)/((2 x - 1) Sqrt[x^4 + x]), x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/3e2b2e9a0f017c78.png)
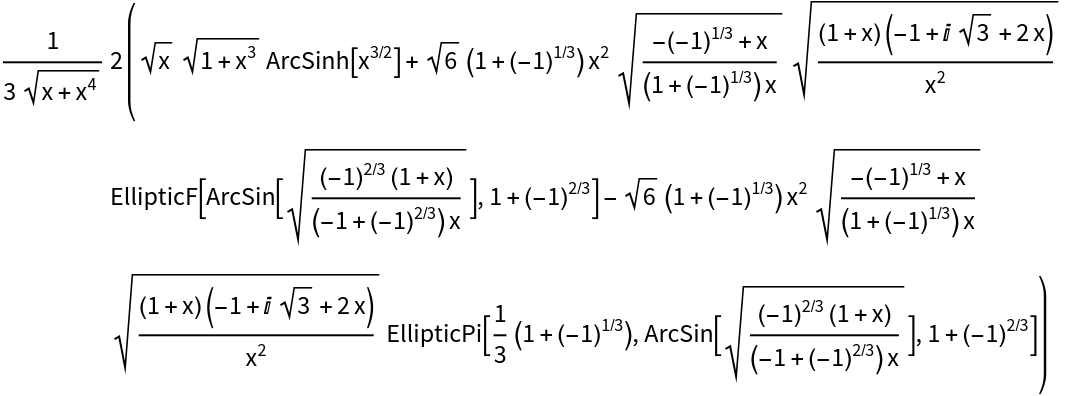
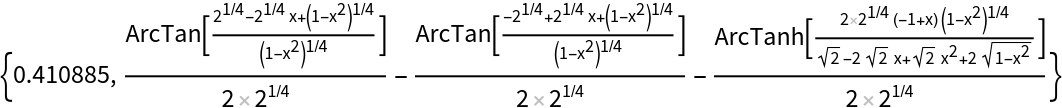
![Integrate[(
x^2 (3 + 2 x^2) (1 + x^2 + 2 x^6))/((1 + x^2)^2 Sqrt[1 + x^2 + x^6]),
x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/063e4592a1e5fd27.png)
![ResourceFunction["IntegrateAlgebraic"][(
x^2 (3 + 2 x^2) (1 + x^2 + 2 x^6))/((1 + x^2)^2 Sqrt[1 + x^2 + x^6]),
x]](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/6b63e2afbbd5b7ae.png)
![\!\(
\*SubscriptBox[\(\[PartialD]\), \(x\)]\((
\*FractionBox[\(1\), \(18\)]\ ArcTan[
\*FractionBox[\(1 - 2\ x +
\*SuperscriptBox[\(x\), \(2\)]\), \(3\
\*SqrtBox[\(\(-1\) +
\*SuperscriptBox[\(x\), \(3\)]\)]\)]] +
\*FractionBox[\(1\), \(18\)]\ ArcTan[
\*FractionBox[\(1\), \(3\)]\
\*SqrtBox[\(\(-1\) +
\*SuperscriptBox[\(x\), \(3\)]\)]] +
\*FractionBox[\(ArcTanh[
\*FractionBox[\(
\*SqrtBox[\(3\)]\
\*SqrtBox[\(\(-1\) +
\*SuperscriptBox[\(x\), \(3\)]\)]\), \(1 + x +
\*SuperscriptBox[\(x\), \(2\)]\)]]\), \(6\
\*SqrtBox[\(3\)]\)])\)\) // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/27e10c0848753641.png)
![\!\(
\*SubscriptBox[\(\[PartialD]\), \({x}\)]\((\(-Log[1 + x]\) +
\*FractionBox[\(1\), \(6\)]\ Log[43 + 258\ x + 612\
\*SuperscriptBox[\(x\), \(2\)] + 772\
\*SuperscriptBox[\(x\), \(3\)] + 624\
\*SuperscriptBox[\(x\), \(4\)] + 360\
\*SuperscriptBox[\(x\), \(5\)] + 112\
\*SuperscriptBox[\(x\), \(6\)] +
\*SqrtBox[\(1 + 8\ x + 12\
\*SuperscriptBox[\(x\), \(2\)] + 8\
\*SuperscriptBox[\(x\), \(3\)] + 4\
\*SuperscriptBox[\(x\), \(4\)]\)]\ \((\(-11\) - 22\ x + 30\
\*SuperscriptBox[\(x\), \(2\)] + 92\
\*SuperscriptBox[\(x\), \(3\)] + 52\
\*SuperscriptBox[\(x\), \(4\)])\)])\)\) // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/97e/97edc14b-04cd-4dc4-93a2-c3abcd5adc3d/7f366fe24e7d8007.png)